Five-qubit error correcting code

Short description: Type of error correction in quantum computing

Quantum circuit that measures stabilizers in the five qubit error correcting code

The five-qubit error correcting code or the 5,1,3 code, is the smallest quantum error correcting code that can protect a logical qubit from any arbitrary single qubit error. In this code, 5 physical qubits are used to encode the logical qubit. With $X$ and $Z$ being Pauli matrices and $I$ the Identity matrix, this code's generators are $⟨XZZXI,IXZZX,XIXZZ,ZXIXZ⟩$. Its logical operators are $\overline{X}=XXXXX$ and $\overline{Z}=ZZZZZ$. Once the logical qubit is encoded, errors on the physical qubits can be detected via stabilizer measurements. A lookup table that maps the results of the stabilizer measurements to the types and locations of the errors gives the control system of the quantum computer enough information to correct errors.

History

Peter Shor's original quantum error correcting code of 1995 used nine qubits. The five-qubit error correcting code was published independently by two groups in 1996: by Raymond Laflamme, Cesar Miquel, Juan Pablo Paz, and Wojciech H. Zurek and by Charles H. Bennett, David DiVincenzo, John A. Smolin and William Wootters.

Measurements

$\overline{Z}$ Parity measurement circuit

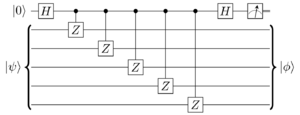
Stabilizer measurements are parity measurements that measure the stabilizers of physical qubits. For example, to measure the first stabilizer ($XZZXI$), a parity measurement of $X$ of the first qubit, $Z$ on the second, $Z$ on the third, $X$ on the fourth, and $I$ on the fifth is performed. Since there are four stabilizers, 4 ancillas will be used to measure them. The first 4 qubits in the image above are the ancillas. The resulting bits from the ancillas is the syndrome; which encodes the type of error that occurred and its location.

A logical qubit can be measured in the computational basis by performing a parity measurement on $\overline{Z}$. If the measured ancilla is $0$, the logical qubit is $|0_{\mathrm{L}}⟩$. If the measured ancilla is $1$, the logical qubit is $|1_{\mathrm{L}}⟩$.

Error correction

It is possible to compute all the single qubit errors that can occur and how to correct them. This is done by calculating what errors commute with the stabilizers. For example, if there is an $X$ error on the first qubit and no errors on the others ($X_1=XIIII$), it commutes with the first stabilizer $[XIIII,XZZXI]=0$. This means that if an X error occurs on the first qubit, the first ancilla qubit will be 0. The second ancilla qubit: $[XIIII,IXZZX]=0$, the third: $[XIIII,XIXZZ]=0$ and the fourth $[XIIII,ZXIXZ]\ne 0$. So if an X error occurs on the first qubit, the syndrome will be $0001$; which is shown in the table below, to the right of $X_1$. Similar calculations are realized for all other possible errors to fill out the table.

$X_1$	0001	$Z_1$	1010	$Y_1$	1011
$X_2$	1000	$Z_2$	0101	$Y_2$	1101
$X_3$	1100	$Z_3$	0010	$Y_3$	1110
$X_4$	0110	$Z_4$	1001	$Y_4$	1111
$X_5$	0011	$Z_5$	0100	$Y_5$	0111

To correct an error, the same operation is performed on the physical qubit based on its syndrome. If the syndrome is $0001$, an $X$ gate is applied to the first qubit to reverse the error.

Encoding

The first step in executing error corrected quantum computation is to encode the computer's initial state by transforming the physical qubits into logical codewords. The logical codewords for the five qubit code are

$\begin{array}{rl}|0_{\mathrm{L}}⟩=\frac{1}{4}[& |00000⟩+|10010⟩+|01001⟩+|10100⟩+|01010⟩-|11011⟩-|00110⟩-|11000⟩\\ -& |11101⟩-|00011⟩-|11110⟩-|01111⟩-|10001⟩-|01100⟩-|10111⟩+|00101⟩],\end{array}$

$\begin{array}{rl}|1_{\mathrm{L}}⟩=\frac{1}{4}[& |11111⟩+|01101⟩+|10110⟩+|01011⟩+|10101⟩-|00100⟩-|11001⟩-|00111⟩\\ -& |00010⟩-|11100⟩-|00001⟩-|10000⟩-|01110⟩-|10011⟩-|01000⟩+|11010⟩].\end{array}$

Stabilizer measurements followed by a $\overline{Z}$ measurement can be used to encode a logical qubit into 5 physical qubits. To prepare $|0_{\mathrm{L}}⟩$, perform stabilizer measurements and apply error correction. After error correction, the logical state is guaranteed to be a logical codeword. If the result of measuring $\overline{Z}$ is $0$, the logical state is $|0_{\mathrm{L}}⟩$. If the result is $1$, the logical state is $|1_{\mathrm{L}}⟩$ and applying $\overline{X}$ will transform it into $|0_{\mathrm{L}}⟩$.