Bernstein–Vazirani algorithm

Short description: Quantum algorithm

The Bernstein–Vazirani algorithm, which solves the Bernstein–Vazirani problem, is a quantum algorithm invented by Ethan Bernstein and Umesh Vazirani in 1997. It is a restricted version of the Deutsch–Jozsa algorithm where instead of distinguishing between two different classes of functions, it tries to learn a string encoded in a function. The Bernstein–Vazirani algorithm was designed to prove an oracle separation between complexity classes BQP and BPP.

Problem statement

Given an oracle that implements a function [math]\displaystyle{ f\colon\{0,1\}^n\rightarrow \{0,1\} }[/math] in which [math]\displaystyle{ f(x) }[/math] is promised to be the dot product between [math]\displaystyle{ x }[/math] and a secret string [math]\displaystyle{ s \in \{0,1\}^n }[/math] modulo 2, [math]\displaystyle{ f(x) = x \cdot s = x_1s_1 \oplus x_2s_2 \oplus \cdots \oplus x_ns_n }[/math], find [math]\displaystyle{ s }[/math].

Algorithm

Classically, the most efficient method to find the secret string is by evaluating the function [math]\displaystyle{ n }[/math] times with the input values [math]\displaystyle{ x = 2^{i} }[/math] for all [math]\displaystyle{ i \in \{0, 1, ..., n-1\} }[/math]:

[math]\displaystyle{ \begin{align} f(1000\cdots0_n) & = s_1 \\ f(0100\cdots0_n) & = s_2 \\ f(0010\cdots0_n) & = s_3 \\ & \,\,\,\vdots \\ f(0000\cdots1_n) & = s_n \\ \end{align} }[/math]

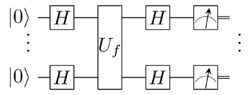
In contrast to the classical solution which needs at least [math]\displaystyle{ n }[/math] queries of the function to find [math]\displaystyle{ s }[/math], only one query is needed using quantum computing. The quantum algorithm is as follows:

Apply a Hadamard transform to the [math]\displaystyle{ n }[/math] qubit state [math]\displaystyle{ |0\rangle^{\otimes n} }[/math] to get

[math]\displaystyle{ \frac{1}{\sqrt{2^{n}}}\sum_{x=0}^{2^n-1} |x\rangle. }[/math]

Next, apply the oracle [math]\displaystyle{ U_f }[/math] which transforms [math]\displaystyle{ |x\rangle \to (-1)^{f(x)}|x\rangle }[/math]. This can be simulated through the standard oracle that transforms [math]\displaystyle{ |b\rangle|x\rangle \to |b \oplus f(x)\rangle |x\rangle }[/math] by applying this oracle to [math]\displaystyle{ \frac{|0\rangle - |1\rangle}{\sqrt{2}}|x\rangle }[/math]. ([math]\displaystyle{ \oplus }[/math] denotes addition mod two.) This transforms the superposition into

[math]\displaystyle{ \frac{1}{\sqrt{2^{n}}}\sum_{x=0}^{2^n-1} (-1)^{f(x)} |x\rangle. }[/math]

Another Hadamard transform is applied to each qubit which makes it so that for qubits where [math]\displaystyle{ s_i = 1 }[/math], its state is converted from [math]\displaystyle{ |-\rangle }[/math] to [math]\displaystyle{ |1\rangle }[/math] and for qubits where [math]\displaystyle{ s_i = 0 }[/math], its state is converted from [math]\displaystyle{ |+\rangle }[/math] to [math]\displaystyle{ |0\rangle }[/math]. To obtain [math]\displaystyle{ s }[/math], a measurement in the standard basis ([math]\displaystyle{ \{|0\rangle, |1\rangle\} }[/math]) is performed on the qubits.

Graphically, the algorithm may be represented by the following diagram, where [math]\displaystyle{ H^{\otimes n} }[/math] denotes the Hadamard transform on [math]\displaystyle{ n }[/math] qubits:

[math]\displaystyle{ |0\rangle^n \xrightarrow{H^{\otimes n }} \frac{1}{\sqrt{2^n}} \sum_{x \in \{0,1\}^n} |x\rangle \xrightarrow{U_f} \frac{1}{\sqrt{2^n}}\sum_{x \in \{0,1\}^n}(-1)^{f(x)}|x\rangle \xrightarrow{H^{\otimes n}} \frac{1}{2^n} \sum_{x,y \in \{0,1\}^n}(-1)^{f(x) + x\cdot y}|y\rangle = |s\rangle }[/math]

The reason that the last state is [math]\displaystyle{ |s\rangle }[/math] is because, for a particular [math]\displaystyle{ y }[/math],

[math]\displaystyle{ \frac{1}{2^n}\sum_{x \in \{0,1\}^n}(-1)^{f(x) + x\cdot y} = \frac{1}{2^n}\sum_{x \in \{0,1\}^n}(-1)^{x\cdot s + x\cdot y} = \frac{1}{2^n}\sum_{x \in \{0,1\}^n}(-1)^{x\cdot (s \oplus y)} = 1 \text{ if } s \oplus y = \vec{0},\, 0 \text{ otherwise}. }[/math]

Since [math]\displaystyle{ s \oplus y = \vec{0} }[/math] is only true when [math]\displaystyle{ s = y }[/math], this means that the only non-zero amplitude is on [math]\displaystyle{ |s\rangle }[/math]. So, measuring the output of the circuit in the computational basis yields the secret string [math]\displaystyle{ s }[/math].

A generalization of Bernstein–Vazirani problem has been proposed that involves finding one or more secret keys using a probabilistic oracle. This is an interesting problem for which a quantum algorithm can provide efficient solutions with certainty or with a high degree of confidence, while classical algorithms completely fail to solve the problem in the general case.

See also

• Hidden Linear Function problem