Runcic 7-cubes
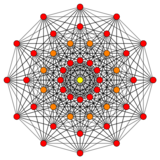 7-demicube Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination
|
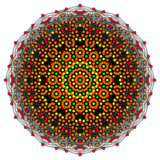 Runcic 7-cube Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination
|
 Runcicantic 7-cube Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination
| |
| Orthogonal projections in D7 Coxeter plane | |||
|---|---|---|---|
In seven-dimensional geometry, a runcic 7-cube is a convex uniform 7-polytope, related to the uniform 7-demicube. There are 2 unique forms.
Runcic 7-cube
| Runcic 7-cube | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,2{3,34,1} h3{4,35} |
| Coxeter-Dynkin diagram | Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination
|
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 16800 |
| Vertices | 2240 |
| Vertex figure | |
| Coxeter groups | D7, [34,1,1] |
| Properties | convex |
A runcic 7-cube, h3{4,35}, has half the vertices of a runcinated 7-cube, t0,3{4,35}.
Alternate names
- Small rhombated hemihepteract (Acronym sirhesa) (Jonathan Bowers)[1]
Cartesian coordinates
The Cartesian coordinates for the vertices of a cantellated demihepteract centered at the origin are coordinate permutations:
- (±1,±1,±1,±3,±3,±3,±3)
with an odd number of plus signs.
Images
Runcicantic 7-cube
| Runcicantic 7-cube | |
|---|---|
| Type | uniform 7-polytope |
| Schläfli symbol | t0,1,2{3,34,1} h2,3{4,35} |
| Coxeter-Dynkin diagram | Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination
|
| 5-faces | |
| 4-faces | |
| Cells | |
| Faces | |
| Edges | 23520 |
| Vertices | 6720 |
| Vertex figure | |
| Coxeter groups | D6, [33,1,1] |
| Properties | convex |
A runcicantic 7-cube, h2,3{4,35}, has half the vertices of a runcicantellated 7-cube, t0,1,3{4,35}.
Alternate names
- Great rhombated hemihepteract (Acronym girhesa) (Jonathan Bowers)[2]
Cartesian coordinates
The Cartesian coordinates for the vertices of a runcicantic 7-cube centered at the origin are coordinate permutations:
- (±1,±1,±1,±1,±3,±5,±5)
with an odd number of plus signs.
Images
Related polytopes
This polytope is based on the 7-demicube, a part of a dimensional family of uniform polytopes called demihypercubes for being alternation of the hypercube family.
There are 95 uniform polytopes with D7 symmetry, 63 are shared by the BC6 symmetry, and 32 are unique:
Notes
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN:978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "7D uniform polytopes (polyexa)". https://bendwavy.org/klitzing/dimensions/polyexa.htm. x3o3o *b3x3o3o3o - sirhesa, x3x3o *b3x3o3o3o - girhesa
External links
- Weisstein, Eric W.. "Hypercube". http://mathworld.wolfram.com/Hypercube.html.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary
Fundamental convex regular and uniform polytopes in dimensions 2–10
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 |

