Uniform 10-polytope

Short description: Type of geometrical object

Graphs of three regular and related uniform polytopes.

10-simplex				Truncated 10-simplex				Rectified 10-simplex
Cantellated 10-simplex						Runcinated 10-simplex
Stericated 10-simplex				Pentellated 10-simplex				Hexicated 10-simplex
Heptellated 10-simplex				Octellated 10-simplex				Ennecated 10-simplex
10-orthoplex				Truncated 10-orthoplex				Rectified 10-orthoplex
10-cube				Truncated 10-cube				Rectified 10-cube
10-demicube						Truncated 10-demicube

In ten-dimensional geometry, a 10-polytope is a 10-dimensional polytope whose boundary consists of 9-polytope facets, exactly two such facets meeting at each 8-polytope ridge.

A uniform 10-polytope is one which is vertex-transitive, and constructed from uniform facets.

Regular 10-polytopes

Regular 10-polytopes can be represented by the Schläfli symbol {p,q,r,s,t,u,v,w,x}, with x {p,q,r,s,t,u,v,w} 9-polytope facets around each peak.

There are exactly three such convex regular 10-polytopes:

1. {3,3,3,3,3,3,3,3,3} - 10-simplex
2. {4,3,3,3,3,3,3,3,3} - 10-cube
3. {3,3,3,3,3,3,3,3,4} - 10-orthoplex

There are no nonconvex regular 10-polytopes.

Euler characteristic

The topology of any given 10-polytope is defined by its Betti numbers and torsion coefficients.

The value of the Euler characteristic used to characterise polyhedra does not generalize usefully to higher dimensions, and is zero for all 10-polytopes, whatever their underlying topology. This inadequacy of the Euler characteristic to reliably distinguish between different topologies in higher dimensions led to the discovery of the more sophisticated Betti numbers.

Similarly, the notion of orientability of a polyhedron is insufficient to characterise the surface twistings of toroidal polytopes, and this led to the use of torsion coefficients.

Uniform 10-polytopes by fundamental Coxeter groups

Uniform 10-polytopes with reflective symmetry can be generated by these three Coxeter groups, represented by permutations of rings of the Coxeter-Dynkin diagrams:

#	Coxeter group		Coxeter-Dynkin diagram
1	A10	[39]
2	B10	[4,38]
3	D10	[37,1,1]

Selected regular and uniform 10-polytopes from each family include:

1. Simplex family: A₁₀ [3⁹] -
   • 527 uniform 10-polytopes as permutations of rings in the group diagram, including one regular:
     1. {3⁹} - 10-simplex -
2. Hypercube/orthoplex family: B₁₀ [4,3⁸] -
   • 1023 uniform 10-polytopes as permutations of rings in the group diagram, including two regular ones:
     1. {4,3⁸} - 10-cube or dekeract -
     2. {3⁸,4} - 10-orthoplex or decacross -
     3. h{4,3⁸} - 10-demicube .
3. Demihypercube D₁₀ family: [3^7,1,1] -
   • 767 uniform 10-polytopes as permutations of rings in the group diagram, including:
     1. 1_7,1 - 10-demicube or demidekeract -
     2. 7_1,1 - 10-orthoplex -

The A₁₀ family

The A₁₀ family has symmetry of order 39,916,800 (11 factorial).

There are 512+16-1=527 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings. 31 are shown below: all one and two ringed forms, and the final omnitruncated form. Bowers-style acronym names are given in parentheses for cross-referencing.

#	Graph	Coxeter-Dynkin diagram Schläfli symbol Name	Element counts
			9-faces	8-faces	7-faces	6-faces	5-faces	4-faces	Cells	Faces	Edges	Vertices
1		t0{3,3,3,3,3,3,3,3,3} 10-simplex (ux)	11	55	165	330	462	462	330	165	55	11
2		t1{3,3,3,3,3,3,3,3,3} Rectified 10-simplex (ru)									495	55
3		t2{3,3,3,3,3,3,3,3,3} Birectified 10-simplex (bru)									1980	165
4		t3{3,3,3,3,3,3,3,3,3} Trirectified 10-simplex (tru)									4620	330
5		t4{3,3,3,3,3,3,3,3,3} Quadrirectified 10-simplex (teru)									6930	462
6		t0,1{3,3,3,3,3,3,3,3,3} Truncated 10-simplex (tu)									550	110
7		t0,2{3,3,3,3,3,3,3,3,3} Cantellated 10-simplex									4455	495
8		t1,2{3,3,3,3,3,3,3,3,3} Bitruncated 10-simplex									2475	495
9		t0,3{3,3,3,3,3,3,3,3,3} Runcinated 10-simplex									15840	1320
10		t1,3{3,3,3,3,3,3,3,3,3} Bicantellated 10-simplex									17820	1980
11		t2,3{3,3,3,3,3,3,3,3,3} Tritruncated 10-simplex									6600	1320
12		t0,4{3,3,3,3,3,3,3,3,3} Stericated 10-simplex									32340	2310
13		t1,4{3,3,3,3,3,3,3,3,3} Biruncinated 10-simplex									55440	4620
14		t2,4{3,3,3,3,3,3,3,3,3} Tricantellated 10-simplex									41580	4620
15		t3,4{3,3,3,3,3,3,3,3,3} Quadritruncated 10-simplex									11550	2310
16		t0,5{3,3,3,3,3,3,3,3,3} Pentellated 10-simplex									41580	2772
17		t1,5{3,3,3,3,3,3,3,3,3} Bistericated 10-simplex									97020	6930
18		t2,5{3,3,3,3,3,3,3,3,3} Triruncinated 10-simplex									110880	9240
19		t3,5{3,3,3,3,3,3,3,3,3} Quadricantellated 10-simplex									62370	6930
20		t4,5{3,3,3,3,3,3,3,3,3} Quintitruncated 10-simplex									13860	2772
21		t0,6{3,3,3,3,3,3,3,3,3} Hexicated 10-simplex									34650	2310
22		t1,6{3,3,3,3,3,3,3,3,3} Bipentellated 10-simplex									103950	6930
23		t2,6{3,3,3,3,3,3,3,3,3} Tristericated 10-simplex									161700	11550
24		t3,6{3,3,3,3,3,3,3,3,3} Quadriruncinated 10-simplex									138600	11550
25		t0,7{3,3,3,3,3,3,3,3,3} Heptellated 10-simplex									18480	1320
26		t1,7{3,3,3,3,3,3,3,3,3} Bihexicated 10-simplex									69300	4620
27		t2,7{3,3,3,3,3,3,3,3,3} Tripentellated 10-simplex									138600	9240
28		t0,8{3,3,3,3,3,3,3,3,3} Octellated 10-simplex									5940	495
29		t1,8{3,3,3,3,3,3,3,3,3} Biheptellated 10-simplex									27720	1980
30		t0,9{3,3,3,3,3,3,3,3,3} Ennecated 10-simplex									990	110
31		t0,1,2,3,4,5,6,7,8,9{3,3,3,3,3,3,3,3,3} Omnitruncated 10-simplex									199584000	39916800

The B₁₀ family

There are 1023 forms based on all permutations of the Coxeter-Dynkin diagrams with one or more rings.

Twelve cases are shown below: ten single-ring (rectified) forms, and two truncations. Bowers-style acronym names are given in parentheses for cross-referencing.

#	Graph	Coxeter-Dynkin diagram Schläfli symbol Name	Element counts
			9-faces	8-faces	7-faces	6-faces	5-faces	4-faces	Cells	Faces	Edges	Vertices
1		t0{4,3,3,3,3,3,3,3,3} 10-cube (deker)	20	180	960	3360	8064	13440	15360	11520	5120	1024
2		t0,1{4,3,3,3,3,3,3,3,3} Truncated 10-cube (tade)									51200	10240
3		t1{4,3,3,3,3,3,3,3,3} Rectified 10-cube (rade)									46080	5120
4		t2{4,3,3,3,3,3,3,3,3} Birectified 10-cube (brade)									184320	11520
5		t3{4,3,3,3,3,3,3,3,3} Trirectified 10-cube (trade)									322560	15360
6		t4{4,3,3,3,3,3,3,3,3} Quadrirectified 10-cube (terade)									322560	13440
7		t4{3,3,3,3,3,3,3,3,4} Quadrirectified 10-orthoplex (terake)									201600	8064
8		t3{3,3,3,3,3,3,3,4} Trirectified 10-orthoplex (trake)									80640	3360
9		t2{3,3,3,3,3,3,3,3,4} Birectified 10-orthoplex (brake)									20160	960
10		t1{3,3,3,3,3,3,3,3,4} Rectified 10-orthoplex (rake)									2880	180
11		t0,1{3,3,3,3,3,3,3,3,4} Truncated 10-orthoplex (take)									3060	360
12		t0{3,3,3,3,3,3,3,3,4} 10-orthoplex (ka)	1024	5120	11520	15360	13440	8064	3360	960	180	20

The D₁₀ family

The D₁₀ family has symmetry of order 1,857,945,600 (10 factorial × 2⁹).

This family has 3×256−1=767 Wythoffian uniform polytopes, generated by marking one or more nodes of the D₁₀ Coxeter-Dynkin diagram. Of these, 511 (2×256−1) are repeated from the B₁₀ family and 256 are unique to this family, with 2 listed below. Bowers-style acronym names are given in parentheses for cross-referencing.

#	Graph	Coxeter-Dynkin diagram Schläfli symbol Name	Element counts
			9-faces	8-faces	7-faces	6-faces	5-faces	4-faces	Cells	Faces	Edges	Vertices
1		10-demicube (hede)	532	5300	24000	64800	115584	142464	122880	61440	11520	512
2		Truncated 10-demicube (thede)									195840	23040

Regular and uniform honeycombs

There are four fundamental affine Coxeter groups that generate regular and uniform tessellations in 9-space:

#	Coxeter group		Coxeter-Dynkin diagram
1	[math]\displaystyle{ {\tilde{A}}_9 }[/math]	[3[10]]
2	[math]\displaystyle{ {\tilde{B}}_9 }[/math]	[4,37,4]
3	[math]\displaystyle{ {\tilde{C}}_9 }[/math]	h[4,37,4] [4,36,31,1]
4	[math]\displaystyle{ {\tilde{D}}_9 }[/math]	q[4,37,4] [31,1,35,31,1]

Regular and uniform tessellations include:

• Regular 9-hypercubic honeycomb, with symbols {4,3⁷,4},
• Uniform alternated 9-hypercubic honeycomb with symbols h{4,3⁷,4},

Regular and uniform hyperbolic honeycombs

There are no compact hyperbolic Coxeter groups of rank 10, groups that can generate honeycombs with all finite facets, and a finite vertex figure. However, there are 3 paracompact hyperbolic Coxeter groups of rank 9, each generating uniform honeycombs in 9-space as permutations of rings of the Coxeter diagrams.

[math]\displaystyle{ {\bar{Q}}_9 }[/math] = [31,1,34,32,1]:

[math]\displaystyle{ {\bar{S}}_9 }[/math] = [4,35,32,1]:

[math]\displaystyle{ E_{10} }[/math] or [math]\displaystyle{ {\bar{T}}_9 }[/math] = [36,2,1]:

Three honeycombs from the [math]\displaystyle{ E_{10} }[/math] family, generated by end-ringed Coxeter diagrams are:

• 6₂₁ honeycomb:
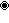
• 2₆₁ honeycomb:
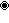
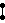
• 1₆₂ honeycomb:

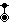
References

• T. Gosset: On the Regular and Semi-Regular Figures in Space of n Dimensions, Messenger of Mathematics, Macmillan, 1900
• A. Boole Stott: Geometrical deduction of semiregular from regular polytopes and space fillings, Verhandelingen of the Koninklijke academy van Wetenschappen width unit Amsterdam, Eerste Sectie 11,1, Amsterdam, 1910
• H.S.M. Coxeter:
  • H.S.M. Coxeter, M.S. Longuet-Higgins und J.C.P. Miller: Uniform Polyhedra, Philosophical Transactions of the Royal Society of London, Londne, 1954
  • H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
• Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
  • (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
  • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
• N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
• Klitzing, Richard. "10D uniform polytopes (polyxenna)". https://bendwavy.org/klitzing/dimensions/polyxenna.htm. 

External links

• Polytope names
• Polytopes of Various Dimensions, Jonathan Bowers
• Multi-dimensional Glossary
• Glossary for hyperspace, George Olshevsky.