Partial least squares regression
| Part of a series on |
| Regression analysis |
|---|
 |
| Models |
| Estimation |
| Background |
|
|
Partial least squares regression (PLS regression) is a statistical method that bears some relation to principal components regression; instead of finding hyperplanes of maximum variance between the response and independent variables, it finds a linear regression model by projecting the predicted variables and the observable variables to a new space. Because both the X and Y data are projected to new spaces, the PLS family of methods are known as bilinear factor models. Partial least squares discriminant analysis (PLS-DA) is a variant used when the Y is categorical.
PLS is used to find the fundamental relations between 2 matrices (X and Y), i.e. a latent variable approach to modeling the covariance structures in these two spaces. A PLS model will try to find the multidimensional direction in the X space that explains the maximum multidimensional variance direction in the Y space. PLS regression is particularly suited when the matrix of predictors has more variables than observations, and when there is multicollinearity among X values. By contrast, standard regression will fail in these cases (unless it is regularized).
Partial least squares was introduced by the Swedish statistician Herman O. A. Wold, who then developed it with his son, Svante Wold. An alternative term for PLS is projection to latent structures,[1][2] but the term partial least squares is still dominant in many areas. Although the original applications were in the social sciences, PLS regression is today most widely used in chemometrics and related areas. It is also used in bioinformatics, sensometrics, neuroscience, and anthropology.
Core Idea

Given [math]\displaystyle{ n }[/math] paired random samples [math]\displaystyle{ (\vec{x}_i, \vec{y}_i), i \in {1,...,n} }[/math]. In the first step [math]\displaystyle{ j=1 }[/math], the partial least squares regression searches for the normalized direction [math]\displaystyle{ \vec{p}_j }[/math], [math]\displaystyle{ \vec{q}_j }[/math] such that the correlation is maximized[3] [math]\displaystyle{ \max_{\vec{p}_j, \vec{q}_j}E_{\vec{X},\vec{Y}}[\underbrace{(\vec{p}_j\cdot \vec{X})}_{t_j} \underbrace{(\vec{q}_j\cdot \vec{Y})}_{u_j} ] }[/math]. Note below, the algorithm is denoted in matrix notation.
Underlying model
The general underlying model of multivariate PLS with [math]\displaystyle{ l }[/math] components is
- [math]\displaystyle{ X = T P^\mathrm{T} + E }[/math]
- [math]\displaystyle{ Y = U Q^\mathrm{T} + F }[/math]
where
- X is an [math]\displaystyle{ n \times m }[/math] matrix of predictors
- Y is an [math]\displaystyle{ n \times p }[/math] matrix of responses
- T and U are [math]\displaystyle{ n \times l }[/math] matrices that are, respectively, projections of X (the X score, component or factor matrix) and projections of Y (the Y scores)
- P and Q are, respectively, [math]\displaystyle{ m \times l }[/math] and [math]\displaystyle{ p \times l }[/math] loading matrices
- and matrices E and F are the error terms, assumed to be independent and identically distributed random normal variables.
The decompositions of X and Y are made so as to maximise the covariance between T and U.
Note that this covariance is defined pair by pair: the covariance of column i of T (length n) with the column i of U (length n) is maximized. Additionally, the covariance of the column i of T with the column j of U (with [math]\displaystyle{ i \not= j }[/math]) is zero.
In PLSR, the loadings are thus chosen so that the scores form an orthogonal basis. This is a major difference with PCA where orthogonality is imposed onto loadings (and not the scores).
Algorithms
A number of variants of PLS exist for estimating the factor and loading matrices T, U, P and Q. Most of them construct estimates of the linear regression between X and Y as [math]\displaystyle{ Y = X \tilde{B} + \tilde{B}_0 }[/math]. Some PLS algorithms are only appropriate for the case where Y is a column vector, while others deal with the general case of a matrix Y. Algorithms also differ on whether they estimate the factor matrix T as an orthogonal (that is, orthonormal) matrix or not.[4][5][6][7][8][9] The final prediction will be the same for all these varieties of PLS, but the components will differ.
PLS is composed of iteratively repeating the following steps k times (for k components):
- finding the directions of maximal covariance in input and output space
- performing least squares regression on the input score
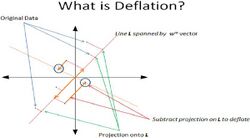
- deflating the input [math]\displaystyle{ X }[/math] and/or target [math]\displaystyle{ Y }[/math]
PLS1
PLS1 is a widely used algorithm appropriate for the vector Y case. It estimates T as an orthonormal matrix. (Caution: the t vectors in the code below may not be normalized appropriately; see talk.) In pseudocode it is expressed below (capital letters are matrices, lower case letters are vectors if they are superscripted and scalars if they are subscripted).
1 function PLS1(X, y, l) 2 [math]\displaystyle{ X^{(0)} \gets X }[/math] 3 [math]\displaystyle{ w^{(0)} \gets X^\mathrm{T} y/\|X^\mathrm{T}y\| }[/math], an initial estimate of w. 4 for [math]\displaystyle{ k = 0 }[/math] to [math]\displaystyle{ l-1 }[/math] 5 [math]\displaystyle{ t^{(k)} \gets X^{(k)}w^{(k)} }[/math] 6 [math]\displaystyle{ t_k \gets {t^{(k)}}^\mathrm{T} t^{(k)} }[/math] (note this is a scalar) 7 [math]\displaystyle{ t^{(k)} \gets t^{(k)} / t_k }[/math] 8 [math]\displaystyle{ p^{(k)} \gets {X^{(k)}}^\mathrm{T} t^{(k)} }[/math] 9 [math]\displaystyle{ q_k \gets {y}^\mathrm{T} t^{(k)} }[/math] (note this is a scalar) 10 if [math]\displaystyle{ q_k = 0 }[/math] 11 [math]\displaystyle{ l \gets k }[/math], break the for loop 12 if [math]\displaystyle{ k \lt (l-1) }[/math] 13 [math]\displaystyle{ X^{(k+1)} \gets X^{(k)} - t_k t^{(k)} {p^{(k)}}^\mathrm{T} }[/math] 14 [math]\displaystyle{ w^{(k+1)} \gets {X^{(k+1)}}^\mathrm{T} y }[/math] 15 end for 16 define W to be the matrix with columns [math]\displaystyle{ w^{(0)},w^{(1)},...,w^{(l-1)} }[/math]. Do the same to form the P matrix and q vector. 17 [math]\displaystyle{ B \gets W {(P^\mathrm{T} W)}^{-1} q }[/math] 18 [math]\displaystyle{ B_0 \gets q_0 - {P^{(0)}}^\mathrm{T} B }[/math] 19 return [math]\displaystyle{ B, B_0 }[/math]
This form of the algorithm does not require centering of the input X and Y, as this is performed implicitly by the algorithm. This algorithm features 'deflation' of the matrix X (subtraction of [math]\displaystyle{ t_k t^{(k)} {p^{(k)}}^\mathrm{T} }[/math]), but deflation of the vector y is not performed, as it is not necessary (it can be proved that deflating y yields the same results as not deflating[10]). The user-supplied variable l is the limit on the number of latent factors in the regression; if it equals the rank of the matrix X, the algorithm will yield the least squares regression estimates for B and [math]\displaystyle{ B_0 }[/math]
Extensions
OPLS
In 2002 a new method was published called orthogonal projections to latent structures (OPLS). In OPLS, continuous variable data is separated into predictive and uncorrelated (orthogonal) information. This leads to improved diagnostics, as well as more easily interpreted visualization. However, these changes only improve the interpretability, not the predictivity, of the PLS models.[11] Similarly, OPLS-DA (Discriminant Analysis) may be applied when working with discrete variables, as in classification and biomarker studies.
The general underlying model of OPLS is
- [math]\displaystyle{ X = T P^\mathrm{T} +T_\text{Y-orth} P^\mathrm{T}_\text{Y-orth} + E }[/math]
- [math]\displaystyle{ Y = U Q^\mathrm{T} + F }[/math]
or in O2-PLS[12]
- [math]\displaystyle{ X = T P^\mathrm{T} +T_\text{Y-orth} P^\mathrm{T}_\text{Y-orth} + E }[/math]
- [math]\displaystyle{ Y = U Q^\mathrm{T} +U_\text{X-orth} Q^\mathrm{T}_\text{X-orth} + F }[/math]
L-PLS
Another extension of PLS regression, named L-PLS for its L-shaped matrices, connects 3 related data blocks to improve predictability.[13] In brief, a new Z matrix, with the same number of columns as the X matrix, is added to the PLS regression analysis and may be suitable for including additional background information on the interdependence of the predictor variables.
3PRF
In 2015 partial least squares was related to a procedure called the three-pass regression filter (3PRF).[14] Supposing the number of observations and variables are large, the 3PRF (and hence PLS) is asymptotically normal for the "best" forecast implied by a linear latent factor model. In stock market data, PLS has been shown to provide accurate out-of-sample forecasts of returns and cash-flow growth.[15]
Partial Least Square SVD
A PLS version based on singular value decomposition (SVD) provides a memory efficient implementation that can be used to address high-dimensional problems, such as relating millions of genetic markers to thousands of imaging features in imaging genetics, on consumer-grade hardware.[16]
PLS correlation
PLS correlation (PLSC) is another methodology related to PLS regression,[17] which has been used in neuroimaging [17][18][19] and sport science,[20] to quantify the strength of the relationship between data sets. Typically, PLSC divides the data into two blocks (sub-groups) each containing one or more variables, and then uses singular value decomposition (SVD) to establish the strength of any relationship (i.e. the amount of shared information) that might exist between the two component sub-groups.[21] It does this by using SVD to determine the inertia (i.e. the sum of the singular values) of the covariance matrix of the sub-groups under consideration.[21][17]
See also
- Canonical correlation
- Data mining
- Deming regression
- Feature extraction
- Machine learning
- Partial least squares path modeling
- Principal component analysis
- Regression analysis
- Total sum of squares
- Projection pursuit regression
References
- ↑ Wold, S; Sjöström, M.; Eriksson, L. (2001). "PLS-regression: a basic tool of chemometrics". Chemometrics and Intelligent Laboratory Systems 58 (2): 109–130. doi:10.1016/S0169-7439(01)00155-1.
- ↑ Abdi, Hervé (2010). "Partial least squares regression and projection on latent structure regression (PLS Regression)". WIREs Computational Statistics 2: 97–106. doi:10.1002/wics.51. https://wires.onlinelibrary.wiley.com/doi/epdf/10.1002/wics.51.
- ↑ See lecture https://www.youtube.com/watch?v=Px2otK2nZ1c&t=46s
- ↑ Lindgren, F; Geladi, P; Wold, S (1993). "The kernel algorithm for PLS". J. Chemometrics 7: 45–59. doi:10.1002/cem.1180070104.
- ↑ de Jong, S.; ter Braak, C.J.F. (1994). "Comments on the PLS kernel algorithm". J. Chemometrics 8 (2): 169–174. doi:10.1002/cem.1180080208.
- ↑ Dayal, B.S.; MacGregor, J.F. (1997). "Improved PLS algorithms". J. Chemometrics 11 (1): 73–85. doi:10.1002/(SICI)1099-128X(199701)11:1<73::AID-CEM435>3.0.CO;2-#.
- ↑ de Jong, S. (1993). "SIMPLS: an alternative approach to partial least squares regression". Chemometrics and Intelligent Laboratory Systems 18 (3): 251–263. doi:10.1016/0169-7439(93)85002-X.
- ↑ Rannar, S.; Lindgren, F.; Geladi, P.; Wold, S. (1994). "A PLS Kernel Algorithm for Data Sets with Many Variables and Fewer Objects. Part 1: Theory and Algorithm". J. Chemometrics 8 (2): 111–125. doi:10.1002/cem.1180080204.
- ↑ Abdi, H. (2010). "Partial least squares regression and projection on latent structure regression (PLS-Regression)". Wiley Interdisciplinary Reviews: Computational Statistics 2: 97–106. doi:10.1002/wics.51.
- ↑ Höskuldsson, Agnar (1988). "PLS Regression Methods". Journal of Chemometrics 2 (3): 219. doi:10.1002/cem.1180020306.
- ↑ Trygg, J; Wold, S (2002). "Orthogonal Projections to Latent Structures". Journal of Chemometrics 16 (3): 119–128. doi:10.1002/cem.695.
- ↑ Eriksson, S. Wold, and J. Tryg. "O2PLS® for improved analysis and visualization of complex data." https://www.dynacentrix.com/telecharg/SimcaP/O2PLS.pdf
- ↑ Sæbøa, S.; Almøya, T.; Flatbergb, A.; Aastveita, A.H.; Martens, H. (2008). "LPLS-regression: a method for prediction and classification under the influence of background information on predictor variables". Chemometrics and Intelligent Laboratory Systems 91 (2): 121–132. doi:10.1016/j.chemolab.2007.10.006.
- ↑ Kelly, Bryan; Pruitt, Seth (2015-06-01). "The three-pass regression filter: A new approach to forecasting using many predictors". Journal of Econometrics. High Dimensional Problems in Econometrics 186 (2): 294–316. doi:10.1016/j.jeconom.2015.02.011.
- ↑ Kelly, Bryan; Pruitt, Seth (2013-10-01). "Market Expectations in the Cross-Section of Present Values". The Journal of Finance 68 (5): 1721–1756. doi:10.1111/jofi.12060. ISSN 1540-6261.
- ↑ Lorenzi, Marco; Altmann, Andre; Gutman, Boris; Wray, Selina; Arber, Charles; Hibar, Derrek P.; Jahanshad, Neda; Schott, Jonathan M. et al. (2018-03-20). "Susceptibility of brain atrophy to TRIB3 in Alzheimer's disease, evidence from functional prioritization in imaging genetics". Proceedings of the National Academy of Sciences 115 (12): 3162–3167. doi:10.1073/pnas.1706100115. ISSN 0027-8424. PMID 29511103.
- ↑ Jump up to: 17.0 17.1 17.2 Krishnan, Anjali; Williams, Lynne J.; McIntosh, Anthony Randal; Abdi, Hervé (May 2011). "Partial Least Squares (PLS) methods for neuroimaging: A tutorial and review". NeuroImage 56 (2): 455–475. doi:10.1016/j.neuroimage.2010.07.034. PMID 20656037.
- ↑ McIntosh, Anthony R.; Mišić, Bratislav (2013-01-03). "Multivariate Statistical Analyses for Neuroimaging Data". Annual Review of Psychology 64 (1): 499–525. doi:10.1146/annurev-psych-113011-143804. ISSN 0066-4308. PMID 22804773.
- ↑ Beggs, Clive B.; Magnano, Christopher; Belov, Pavel; Krawiecki, Jacqueline; Ramasamy, Deepa P.; Hagemeier, Jesper; Zivadinov, Robert (2016-05-02). de Castro, Fernando. ed. "Internal Jugular Vein Cross-Sectional Area and Cerebrospinal Fluid Pulsatility in the Aqueduct of Sylvius: A Comparative Study between Healthy Subjects and Multiple Sclerosis Patients". PLOS ONE 11 (5): e0153960. doi:10.1371/journal.pone.0153960. ISSN 1932-6203. PMID 27135831. Bibcode: 2016PLoSO..1153960B.
- ↑ Weaving, Dan; Jones, Ben; Ireton, Matt; Whitehead, Sarah; Till, Kevin; Beggs, Clive B. (2019-02-14). Connaboy, Chris. ed. "Overcoming the problem of multicollinearity in sports performance data: A novel application of partial least squares correlation analysis". PLOS ONE 14 (2): e0211776. doi:10.1371/journal.pone.0211776. ISSN 1932-6203. PMID 30763328. Bibcode: 2019PLoSO..1411776W.
- ↑ Jump up to: 21.0 21.1 Abdi, Hervé; Williams, Lynne J. (2013), Reisfeld, Brad; Mayeno, Arthur N., eds., "Partial Least Squares Methods: Partial Least Squares Correlation and Partial Least Square Regression", Computational Toxicology (Humana Press) 930: pp. 549–579, doi:10.1007/978-1-62703-059-5_23, ISBN 9781627030588, PMID 23086857
Literature
- Kramer, R. (1998). Chemometric Techniques for Quantitative Analysis. Marcel-Dekker. ISBN 978-0-8247-0198-7.
- Frank, Ildiko E.; Friedman, Jerome H. (1993). "A Statistical View of Some Chemometrics Regression Tools". Technometrics 35 (2): 109–148. doi:10.1080/00401706.1993.10485033.
- Haenlein, Michael; Kaplan, Andreas M. (2004). "A Beginner's Guide to Partial Least Squares Analysis". Understanding Statistics 3 (4): 283–297. doi:10.1207/s15328031us0304_4.
- Henseler, Joerg; Fassott, Georg (2005). Testing Moderating Effects in PLS Path Models. An Illustration of Available Procedures.
- Lingjærde, Ole-Christian; Christophersen, Nils (2000). "Shrinkage Structure of Partial Least Squares". Scandinavian Journal of Statistics 27 (3): 459–473. doi:10.1111/1467-9469.00201.
- Tenenhaus, Michel (1998). La Régression PLS: Théorie et Pratique. Paris: Technip..
- Rosipal, Roman; Kramer, Nicole (2006). Overview and Recent Advances in Partial Least Squares, in Subspace, Latent Structure and Feature Selection Techniques. pp. 34–51.
- Helland, Inge S. (1990). "PLS regression and statistical models". Scandinavian Journal of Statistics 17 (2): 97–114.
- Wold, Herman (1966). "Estimation of principal components and related models by iterative least squares". in Krishnaiaah, P.R.. Multivariate Analysis. New York: Academic Press. pp. 391–420.
- Wold, Herman (1981). The fix-point approach to interdependent systems. Amsterdam: North Holland.
- Wold, Herman (1985). "Partial least squares". in Kotz, Samuel; Johnson, Norman L.. Encyclopedia of statistical sciences. 6. New York: Wiley. pp. 581–591.
- Wold, Svante; Ruhe, Axel; Wold, Herman; Dunn, W.J. (1984). "The collinearity problem in linear regression. the partial least squares (PLS) approach to generalized inverses". SIAM Journal on Scientific and Statistical Computing 5 (3): 735–743. doi:10.1137/0905052.
- Garthwaite, Paul H. (1994). "An Interpretation of Partial Least Squares". Journal of the American Statistical Association 89 (425): 122–7. doi:10.1080/01621459.1994.10476452.
- Wang, H., ed (2010). Handbook of Partial Least Squares. ISBN 978-3-540-32825-4.
- Stone, M.; Brooks, R.J. (1990). "Continuum Regression: Cross-Validated Sequentially Constructed Prediction embracing Ordinary Least Squares, Partial Least Squares and Principal Components Regression". Journal of the Royal Statistical Society, Series B 52 (2): 237–269.
External links
Please be cautious adding more external links.
Wikipedia is not a collection of links and should not be used for advertising.
Excessive or inappropriate links will be removed.
See Wikipedia:External links and Wikipedia:Spam for details.
If there are already suitable links, propose additions or replacements on the article's talk page.
-->
- A short introduction to PLS regression and its history
- Video: Derivation of PLS by Prof. H. Harry Asada
 |