Linear least squares

Short description: Least squares approximation of linear functions to data

Linear least squares (LLS) is the least squares approximation of linear functions to data. It is a set of formulations for solving statistical problems involved in linear regression, including variants for ordinary (unweighted), weighted, and generalized (correlated) residuals. Numerical methods for linear least squares include inverting the matrix of the normal equations and orthogonal decomposition methods.

Basic formulation

Consider the linear equation

[math]\displaystyle{ Ax = b, }[/math]

(1)

where [math]\displaystyle{ A \in \mathbb{R}^{m\times n} }[/math] and [math]\displaystyle{ b \in \mathbb{R}^m }[/math] are given and [math]\displaystyle{ x \in \mathbb{R}^n }[/math] is variable to be computed. When [math]\displaystyle{ m \gt n, }[/math] it is generally the case that (1) has no solution. For example, there is no value of [math]\displaystyle{ x }[/math] that satisfies [math]\displaystyle{ \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{bmatrix} x = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}, }[/math] because the first two rows require that [math]\displaystyle{ x = (1, 1), }[/math] but then the third row is not satisfied. Thus, for [math]\displaystyle{ m \gt n, }[/math] the goal of solving (1) exactly is typically replaced by finding the value of [math]\displaystyle{ x }[/math] that minimizes some error. There are many ways that the error can be defined, but one of the most common is to define it as [math]\displaystyle{ \|Ax - b\|^2. }[/math] This produces a minimization problem, called a least squares problem

[math]\displaystyle{ \begin{aligned} \underset{x \in \mathbb{R}^m}{\operatorname{minimize}} \quad & \|Ax - b\|^2. \end{aligned} }[/math]

(2)

The solution to the least squares problem (1) is computed by solving the normal equation

[math]\displaystyle{ A^\top A x = A^\top b, }[/math]

(3)

where [math]\displaystyle{ A^\top }[/math] denotes the transpose of [math]\displaystyle{ A }[/math].

Continuing the example, above, with [math]\displaystyle{ A = \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{bmatrix} \quad \text{and} \quad b = \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix}, }[/math] we find [math]\displaystyle{ A^\top A = \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 \\ 0 & 1 \\ 1 & 1 \end{bmatrix} = \begin{bmatrix} 2 & 1 \\ 1 & 2 \end{bmatrix} }[/math] and [math]\displaystyle{ A^\top b = \begin{bmatrix} 1 & 0 & 1\\ 0 & 1 & 1 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \\ 0 \end{bmatrix} = \begin{bmatrix} 1 \\ 1 \end{bmatrix}. }[/math] Solving the normal equation gives [math]\displaystyle{ x = (1/3, 1/3). }[/math]

Formulations for Linear Regression

The three main linear least squares formulations are:

• Ordinary least squares (OLS) is the most common estimator. OLS estimates are commonly used to analyze both experimental and observational data.
  The OLS method minimizes the sum of squared residuals, and leads to a closed-form expression for the estimated value of the unknown parameter vector β: [math]\displaystyle{ \hat{\boldsymbol\beta} = (\mathbf{X}^\mathsf{T}\mathbf{X})^{-1} \mathbf{X}^\mathsf{T} \mathbf{y}, }[/math] where [math]\displaystyle{ \mathbf{y} }[/math] is a vector whose ith element is the ith observation of the dependent variable, and [math]\displaystyle{ \mathbf{X} }[/math] is a matrix whose ij element is the ith observation of the jth independent variable. The estimator is unbiased and consistent if the errors have finite variance and are uncorrelated with the regressors: [math]\displaystyle{ \operatorname{E}[\,\mathbf{x}_i\varepsilon_i\,] = 0, }[/math] where [math]\displaystyle{ \mathbf{x}_i }[/math] is the transpose of row i of the matrix [math]\displaystyle{ \mathbf{X}. }[/math] It is also efficient under the assumption that the errors have finite variance and are homoscedastic, meaning that E[ε_i²|x_i] does not depend on i. The condition that the errors are uncorrelated with the regressors will generally be satisfied in an experiment, but in the case of observational data, it is difficult to exclude the possibility of an omitted covariate z that is related to both the observed covariates and the response variable. The existence of such a covariate will generally lead to a correlation between the regressors and the response variable, and hence to an inconsistent estimator of β. The condition of homoscedasticity can fail with either experimental or observational data. If the goal is either inference or predictive modeling, the performance of OLS estimates can be poor if multicollinearity is present, unless the sample size is large.
• Weighted least squares (WLS) are used when heteroscedasticity is present in the error terms of the model.
• Generalized least squares (GLS) is an extension of the OLS method, that allows efficient estimation of β when either heteroscedasticity, or correlations, or both are present among the error terms of the model, as long as the form of heteroscedasticity and correlation is known independently of the data. To handle heteroscedasticity when the error terms are uncorrelated with each other, GLS minimizes a weighted analogue to the sum of squared residuals from OLS regression, where the weight for the i^th case is inversely proportional to var(ε_i). This special case of GLS is called "weighted least squares". The GLS solution to an estimation problem is [math]\displaystyle{ \hat{\boldsymbol\beta} = (\mathbf{X}^\mathsf{T} \boldsymbol\Omega^{-1} \mathbf{X})^{-1}\mathbf{X}^\mathsf{T}\boldsymbol\Omega^{-1}\mathbf{y}, }[/math] where Ω is the covariance matrix of the errors. GLS can be viewed as applying a linear transformation to the data so that the assumptions of OLS are met for the transformed data. For GLS to be applied, the covariance structure of the errors must be known up to a multiplicative constant.

Alternative formulations

Other formulations include:

• Iteratively reweighted least squares (IRLS) is used when heteroscedasticity, or correlations, or both are present among the error terms of the model, but where little is known about the covariance structure of the errors independently of the data. In the first iteration, OLS, or GLS with a provisional covariance structure is carried out, and the residuals are obtained from the fit. Based on the residuals, an improved estimate of the covariance structure of the errors can usually be obtained. A subsequent GLS iteration is then performed using this estimate of the error structure to define the weights. The process can be iterated to convergence, but in many cases, only one iteration is sufficient to achieve an efficient estimate of β.
• Instrumental variables regression (IV) can be performed when the regressors are correlated with the errors. In this case, we need the existence of some auxiliary instrumental variables z_i such that E[z_iε_i] = 0. If Z is the matrix of instruments, then the estimator can be given in closed form as [math]\displaystyle{ \hat{\boldsymbol\beta} = (\mathbf{X}^\mathsf{T}\mathbf{Z}(\mathbf{Z}^\mathsf{T}\mathbf{Z})^{-1}\mathbf{Z}^\mathsf{T}\mathbf{X})^{-1}\mathbf{X}^\mathsf{T}\mathbf{Z}(\mathbf{Z}^\mathsf{T}\mathbf{Z})^{-1}\mathbf{Z}^\mathsf{T}\mathbf{y}. }[/math] Optimal instruments regression is an extension of classical IV regression to the situation where E[ε_i | z_i] = 0.
• Total least squares (TLS) is an approach to least squares estimation of the linear regression model that treats the covariates and response variable in a more geometrically symmetric manner than OLS. It is one approach to handling the "errors in variables" problem, and is also sometimes used even when the covariates are assumed to be error-free.

• Linear Template Fit (LTF) combines a linear regression with (generalized) least squares in order to determine the best estimator. The Linear Template Fit addresses the frequent issue, when the residuals cannot be expressed analytically or are too time consuming to be evaluate repeatedly, as it is often the case in iterative minimization algorithms. In the Linear Template Fit, the residuals are estimated from the random variables and from a linear approximation of the underlying true model, while the true model needs to be provided for at least [math]\displaystyle{ n+1 }[/math] (were [math]\displaystyle{ n }[/math] is the number of estimators) distinct reference values β. The true distribution is then approximated by a linear regression, and the best estimators are obtained in closed form as [math]\displaystyle{ \hat{\boldsymbol\beta} = ((\mathbf{Y\tilde{M}})^\mathsf{T} \boldsymbol\Omega^{-1} \mathbf{Y\tilde{M}})^{-1}(\mathbf{Y\tilde{M}})^\mathsf{T}\boldsymbol\Omega^{-1}(\mathbf{y}-\mathbf{Y\bar{m})}, }[/math] where [math]\displaystyle{ \mathbf{Y} }[/math] denotes the template matrix with the values of the known or previously determined model for any of the reference values β, [math]\displaystyle{ \mathbf{y} }[/math] are the random variables (e.g. a measurement), and the matrix [math]\displaystyle{ \mathbf{\tilde{M}} }[/math] and the vector [math]\displaystyle{ \mathbf{\tilde{m}} }[/math] are calculated from the values of β. The LTF can also be expressed for Log-normal distribution distributed random variables. A generalization of the LTF is the Quadratic Template Fit, which assumes a second order regression of the model, requires predictions for at least [math]\displaystyle{ n^2+2n }[/math] distinct values β, and it finds the best estimator using Newton's method.

• Percentage least squares focuses on reducing percentage errors, which is useful in the field of forecasting or time series analysis. It is also useful in situations where the dependent variable has a wide range without constant variance, as here the larger residuals at the upper end of the range would dominate if OLS were used. When the percentage or relative error is normally distributed, least squares percentage regression provides maximum likelihood estimates. Percentage regression is linked to a multiplicative error model, whereas OLS is linked to models containing an additive error term.

• Constrained least squares, indicates a linear least squares problem with additional constraints on the solution.

Objective function

In OLS (i.e., assuming unweighted observations), the optimal value of the objective function is found by substituting the optimal expression for the coefficient vector: [math]\displaystyle{ S=\mathbf y^\mathsf{T} (\mathbf{I} - \mathbf{H})^\mathsf{T} (\mathbf{I} - \mathbf{H}) \mathbf y = \mathbf y^\mathsf{T} (\mathbf{I} - \mathbf{H}) \mathbf y, }[/math] where [math]\displaystyle{ \mathbf{H}=\mathbf{X}(\mathbf{X}^\mathsf{T}\mathbf{X})^{-1} \mathbf{X}^\mathsf{T} }[/math], the latter equality holding since [math]\displaystyle{ (\mathbf{I} - \mathbf{H}) }[/math] is symmetric and idempotent. It can be shown from this that under an appropriate assignment of weights the expected value of S is [math]\displaystyle{ m-n }[/math]. If instead unit weights are assumed, the expected value of S is [math]\displaystyle{ (m - n)\sigma^2 }[/math], where [math]\displaystyle{ \sigma^2 }[/math] is the variance of each observation.

If it is assumed that the residuals belong to a normal distribution, the objective function, being a sum of weighted squared residuals, will belong to a chi-squared ([math]\displaystyle{ \chi ^2 }[/math]) distribution with m − n degrees of freedom. Some illustrative percentile values of [math]\displaystyle{ \chi ^2 }[/math] are given in the following table.

[math]\displaystyle{ m - n }[/math]	[math]\displaystyle{ \chi ^2_{0.50} }[/math]	[math]\displaystyle{ \chi ^2 _{0.95} }[/math]	[math]\displaystyle{ \chi ^2 _{0.99} }[/math]
10	9.34	18.3	23.2
25	24.3	37.7	44.3
100	99.3	124	136

These values can be used for a statistical criterion as to the goodness of fit. When unit weights are used, the numbers should be divided by the variance of an observation.

For WLS, the ordinary objective function above is replaced for a weighted average of residuals.

Discussion

In statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model. The resulting fitted model can be used to summarize the data, to predict unobserved values from the same system, and to understand the mechanisms that may underlie the system.

Mathematically, linear least squares is the problem of approximately solving an overdetermined system of linear equations A x = b, where b is not an element of the column space of the matrix A. The approximate solution is realized as an exact solution to A x = b', where b' is the projection of b onto the column space of A. The best approximation is then that which minimizes the sum of squared differences between the data values and their corresponding modeled values. The approach is called linear least squares since the assumed function is linear in the parameters to be estimated. Linear least squares problems are convex and have a closed-form solution that is unique, provided that the number of data points used for fitting equals or exceeds the number of unknown parameters, except in special degenerate situations. In contrast, non-linear least squares problems generally must be solved by an iterative procedure, and the problems can be non-convex with multiple optima for the objective function. If prior distributions are available, then even an underdetermined system can be solved using the Bayesian MMSE estimator.

In statistics, linear least squares problems correspond to a particularly important type of statistical model called linear regression which arises as a particular form of regression analysis. One basic form of such a model is an ordinary least squares model. The present article concentrates on the mathematical aspects of linear least squares problems, with discussion of the formulation and interpretation of statistical regression models and statistical inferences related to these being dealt with in the articles just mentioned. See outline of regression analysis for an outline of the topic.

Properties

If the experimental errors, [math]\displaystyle{ \varepsilon }[/math], are uncorrelated, have a mean of zero and a constant variance, [math]\displaystyle{ \sigma }[/math], the Gauss–Markov theorem states that the least-squares estimator, [math]\displaystyle{ \hat{\boldsymbol{\beta}} }[/math], has the minimum variance of all estimators that are linear combinations of the observations. In this sense it is the best, or optimal, estimator of the parameters. Note particularly that this property is independent of the statistical distribution function of the errors. In other words, the distribution function of the errors need not be a normal distribution. However, for some probability distributions, there is no guarantee that the least-squares solution is even possible given the observations; still, in such cases it is the best estimator that is both linear and unbiased.

For example, it is easy to show that the arithmetic mean of a set of measurements of a quantity is the least-squares estimator of the value of that quantity. If the conditions of the Gauss–Markov theorem apply, the arithmetic mean is optimal, whatever the distribution of errors of the measurements might be.

However, in the case that the experimental errors do belong to a normal distribution, the least-squares estimator is also a maximum likelihood estimator.

These properties underpin the use of the method of least squares for all types of data fitting, even when the assumptions are not strictly valid.

Limitations

An assumption underlying the treatment given above is that the independent variable, x, is free of error. In practice, the errors on the measurements of the independent variable are usually much smaller than the errors on the dependent variable and can therefore be ignored. When this is not the case, total least squares or more generally errors-in-variables models, or rigorous least squares, should be used. This can be done by adjusting the weighting scheme to take into account errors on both the dependent and independent variables and then following the standard procedure.

In some cases the (weighted) normal equations matrix X^TX is ill-conditioned. When fitting polynomials the normal equations matrix is a Vandermonde matrix. Vandermonde matrices become increasingly ill-conditioned as the order of the matrix increases. In these cases, the least squares estimate amplifies the measurement noise and may be grossly inaccurate. Various regularization techniques can be applied in such cases, the most common of which is called ridge regression. If further information about the parameters is known, for example, a range of possible values of [math]\displaystyle{ \mathbf{\hat{\boldsymbol{\beta}}} }[/math], then various techniques can be used to increase the stability of the solution. For example, see constrained least squares.

Another drawback of the least squares estimator is the fact that the norm of the residuals, [math]\displaystyle{ \| \mathbf y - \mathbf X\hat{\boldsymbol{\beta}} \| }[/math] is minimized, whereas in some cases one is truly interested in obtaining small error in the parameter [math]\displaystyle{ \mathbf{\hat{\boldsymbol{\beta}}} }[/math], e.g., a small value of [math]\displaystyle{ \|{\boldsymbol{\beta}}-\hat{\boldsymbol{\beta}}\| }[/math]. However, since the true parameter [math]\displaystyle{ {\boldsymbol{\beta}} }[/math] is necessarily unknown, this quantity cannot be directly minimized. If a prior probability on [math]\displaystyle{ \hat{\boldsymbol{\beta}} }[/math] is known, then a Bayes estimator can be used to minimize the mean squared error, [math]\displaystyle{ E \left\{ \| {\boldsymbol{\beta}} - \hat{\boldsymbol{\beta}} \|^2 \right\} }[/math]. The least squares method is often applied when no prior is known. When several parameters are being estimated jointly, better estimators can be constructed, an effect known as Stein's phenomenon. For example, if the measurement error is Gaussian, several estimators are known which dominate, or outperform, the least squares technique; the best known of these is the James–Stein estimator. This is an example of more general shrinkage estimators that have been applied to regression problems.

Applications

Least square approximation with linear, quadratic and cubic polynomials.

• Polynomial fitting: models are polynomials in an independent variable, x:
  • Straight line: [math]\displaystyle{ f(x, \boldsymbol \beta)=\beta_1 +\beta_2 x }[/math].
  • Quadratic: [math]\displaystyle{ f(x, \boldsymbol \beta)=\beta_1 + \beta_2 x +\beta_3 x^2 }[/math].
  • Cubic, quartic and higher polynomials. For regression with high-order polynomials, the use of orthogonal polynomials is recommended.
• Numerical smoothing and differentiation — this is an application of polynomial fitting.
• Multinomials in more than one independent variable, including surface fitting
• Curve fitting with B-splines
• Chemometrics, Calibration curve, Standard addition, Gran plot, analysis of mixtures

Uses in data fitting

The primary application of linear least squares is in data fitting. Given a set of m data points [math]\displaystyle{ y_1, y_2,\dots, y_m, }[/math] consisting of experimentally measured values taken at m values [math]\displaystyle{ x_1, x_2,\dots, x_m }[/math] of an independent variable ([math]\displaystyle{ x_i }[/math] may be scalar or vector quantities), and given a model function [math]\displaystyle{ y=f(x, \boldsymbol \beta), }[/math] with [math]\displaystyle{ \boldsymbol \beta = (\beta_1, \beta_2, \dots, \beta_n), }[/math] it is desired to find the parameters [math]\displaystyle{ \beta_j }[/math] such that the model function "best" fits the data. In linear least squares, linearity is meant to be with respect to parameters [math]\displaystyle{ \beta_j, }[/math] so [math]\displaystyle{ f(x, \boldsymbol \beta) = \sum_{j=1}^{n} \beta_j \varphi_j(x). }[/math]

Here, the functions [math]\displaystyle{ \varphi_j }[/math] may be nonlinear with respect to the variable x.

Ideally, the model function fits the data exactly, so [math]\displaystyle{ y_i = f(x_i, \boldsymbol \beta) }[/math] for all [math]\displaystyle{ i=1, 2, \dots, m. }[/math] This is usually not possible in practice, as there are more data points than there are parameters to be determined. The approach chosen then is to find the minimal possible value of the sum of squares of the residuals [math]\displaystyle{ r_i(\boldsymbol \beta)= y_i - f(x_i, \boldsymbol \beta),\ (i=1, 2, \dots, m) }[/math] so to minimize the function [math]\displaystyle{ S(\boldsymbol \beta)=\sum_{i=1}^{m}r_i^2(\boldsymbol \beta). }[/math]

After substituting for [math]\displaystyle{ r_i }[/math] and then for [math]\displaystyle{ f }[/math], this minimization problem becomes the quadratic minimization problem above with [math]\displaystyle{ X_{ij} = \varphi_j(x_i), }[/math] and the best fit can be found by solving the normal equations.

Example

A plot of the data points (in red), the least squares line of best fit (in blue), and the residuals (in green)

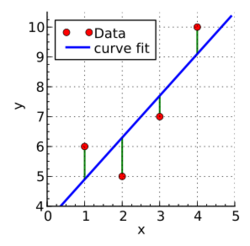
A hypothetical researcher conducts an experiment and obtains four [math]\displaystyle{ (x, y) }[/math] data points: [math]\displaystyle{ (1, 6), }[/math] [math]\displaystyle{ (2, 5), }[/math] [math]\displaystyle{ (3, 7), }[/math] and [math]\displaystyle{ (4, 10) }[/math] (shown in red in the diagram on the right). Because of exploratory data analysis or prior knowledge of the subject matter, the researcher suspects that the [math]\displaystyle{ y }[/math]-values depend on the [math]\displaystyle{ x }[/math]-values systematically. The [math]\displaystyle{ x }[/math]-values are assumed to be exact, but the [math]\displaystyle{ y }[/math]-values contain some uncertainty or "noise", because of the phenomenon being studied, imperfections in the measurements, etc.

Fitting a line

One of the simplest possible relationships between [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] is a line [math]\displaystyle{ y=\beta_1+\beta_2 x }[/math]. The intercept [math]\displaystyle{ \beta_1 }[/math] and the slope [math]\displaystyle{ \beta_2 }[/math] are initially unknown. The researcher would like to find values of [math]\displaystyle{ \beta_1 }[/math] and [math]\displaystyle{ \beta_2 }[/math] that cause the line to pass through the four data points. In other words, the researcher would like to solve the system of linear equations [math]\displaystyle{ \begin{alignat}{3} \beta_1 + 1 \beta_2 &&\; = \;&& 6, & \\ \beta_1 + 2 \beta_2 &&\; = \;&& 5, & \\ \beta_1 + 3 \beta_2 &&\; = \;&& 7, & \\ \beta_1 + 4 \beta_2 &&\; = \;&& 10. & \\ \end{alignat} }[/math] With four equations in two unknowns, this system is overdetermined. There is no exact solution. To consider approximate solutions, one introduces residuals [math]\displaystyle{ r_1 }[/math], [math]\displaystyle{ r_2 }[/math], [math]\displaystyle{ r_3 }[/math], [math]\displaystyle{ r_4 }[/math] into the equations: [math]\displaystyle{ \begin{alignat}{3} \beta_1 + 1 \beta_2 + r_1 &&\; = \;&& 6, & \\ \beta_1 + 2 \beta_2 + r_2 &&\; = \;&& 5, & \\ \beta_1 + 3 \beta_2 + r_3 &&\; = \;&& 7, & \\ \beta_1 + 4 \beta_2 + r_4 &&\; = \;&& 10. & \\ \end{alignat} }[/math] The [math]\displaystyle{ i }[/math]th residual [math]\displaystyle{ r_i }[/math] is the misfit between the [math]\displaystyle{ i }[/math]th observation [math]\displaystyle{ y_i }[/math] and the [math]\displaystyle{ i }[/math]th prediction [math]\displaystyle{ \beta_1 + \beta_2 x_i }[/math]: [math]\displaystyle{ \begin{alignat}{3} r_1 &&\; = \;&& 6 - (\beta_1 + 1\beta_2), & \\ r_2 &&\; = \;&& 5 - (\beta_1 + 2\beta_2), & \\ r_3 &&\; = \;&& 7 - (\beta_1 + 3\beta_2), & \\ r_4 &&\; = \;&& 10 - (\beta_1 + 4\beta_2). & \\ \end{alignat} }[/math] Among all approximate solutions, the researcher would like to find the one that is "best" in some sense.

In least squares, one focuses on the sum [math]\displaystyle{ S }[/math] of the squared residuals: [math]\displaystyle{ \begin{align} S(\beta_1, \beta_2) &= r_1^2 + r_2^2 + r_3^2 + r_4^2 \\[6pt] &= [6-(\beta_1+1\beta_2)]^2 + [5-(\beta_1+2\beta_2)]^2 + [7-(\beta_1+3\beta_2)]^2 + [10-(\beta_1+4\beta_2)]^2 \\[6pt] &= 4\beta_1^2 + 30\beta_2^2 + 20\beta_1\beta_2 - 56\beta_1 - 154\beta_2 + 210. \\[6pt] \end{align} }[/math] The best solution is defined to be the one that minimizes [math]\displaystyle{ S }[/math] with respect to [math]\displaystyle{ \beta_1 }[/math] and [math]\displaystyle{ \beta_2 }[/math]. The minimum can be calculated by setting the partial derivatives of [math]\displaystyle{ S }[/math] to zero: [math]\displaystyle{ 0 = \frac{\partial S}{\partial \beta_1} = 8 \beta_1 + 20 \beta_2 -56, }[/math] [math]\displaystyle{ 0 = \frac{\partial S}{\partial \beta_2} = 20 \beta_1 + 60 \beta_2 -154. }[/math] These normal equations constitute a system of two linear equations in two unknowns. The solution is [math]\displaystyle{ \beta_1 = 3.5 }[/math] and [math]\displaystyle{ \beta_2 = 1.4 }[/math], and the best-fit line is therefore [math]\displaystyle{ y = 3.5 + 1.4x }[/math]. The residuals are [math]\displaystyle{ 1.1, }[/math] [math]\displaystyle{ -1.3, }[/math] [math]\displaystyle{ -0.7, }[/math] and [math]\displaystyle{ 0.9 }[/math] (see the diagram on the right). The minimum value of the sum of squared residuals is [math]\displaystyle{ S(3.5, 1.4) = 1.1^2+(-1.3)^2+(-0.7)^2+0.9^2 = 4.2. }[/math]

This calculation can be expressed in matrix notation as follows. The original system of equations is [math]\displaystyle{ \mathbf{y} = \mathbf{X} \mathbf{\beta} }[/math], where [math]\displaystyle{ \mathbf{y} = \left[\begin{array}{c} 6 \\ 5 \\ 7 \\ 10 \end{array}\right], \;\;\;\; \mathbf{X} = \left[\begin{array}{cc}1 & 1 \\ 1 & 2 \\ 1 & 3 \\ 1 & 4 \end{array}\right], \;\;\;\; \mathbf{\beta} = \left[\begin{array}{c} \beta_1 \\ \beta_2 \end{array}\right]. }[/math] Intuitively, [math]\displaystyle{ \mathbf{y} = \mathbf{X} \mathbf{\beta} \;\;\;\; \Rightarrow \;\;\;\; \mathbf{X}^\top \mathbf{y} = \mathbf{X}^\top \mathbf{X} \mathbf{\beta} \;\;\;\; \Rightarrow \;\;\;\; \mathbf{\beta} = \left(\mathbf{X}^\top \mathbf{X}\right)^{-1} \mathbf{X}^\top \mathbf{y} = \left[\begin{array}{c} 3.5 \\ 1.4 \end{array}\right]. }[/math] More rigorously, if [math]\displaystyle{ \mathbf{X}^\top \mathbf{X} }[/math] is invertible, then the matrix [math]\displaystyle{ \mathbf{X} \left(\mathbf{X}^\top \mathbf{X}\right)^{-1} \mathbf{X}^\top }[/math] represents orthogonal projection onto the column space of [math]\displaystyle{ \mathbf{X} }[/math]. Therefore, among all vectors of the form [math]\displaystyle{ \mathbf{X} \mathbf{\beta} }[/math], the one closest to [math]\displaystyle{ \mathbf{y} }[/math] is [math]\displaystyle{ \mathbf{X} \left(\mathbf{X}^\top \mathbf{X}\right)^{-1} \mathbf{X}^\top \mathbf{y} }[/math]. Setting [math]\displaystyle{ \mathbf{X} \left(\mathbf{X}^\top \mathbf{X}\right)^{-1} \mathbf{X}^\top \mathbf{y} = \mathbf{X} \mathbf{\beta}, }[/math] it is evident that [math]\displaystyle{ \mathbf{\beta} = \left(\mathbf{X}^\top \mathbf{X}\right)^{-1} \mathbf{X}^\top \mathbf{y} }[/math] is a solution.

Fitting a parabola

Further information: Polynomial regression

The result of fitting a quadratic function [math]\displaystyle{ y=\beta_1+\beta_2x+\beta_3x^2\, }[/math] (in blue) through a set of data points [math]\displaystyle{ (x_i, y_i) }[/math] (in red). In linear least squares the function need not be linear in the argument [math]\displaystyle{ x, }[/math] but only in the parameters [math]\displaystyle{ \beta_j }[/math] that are determined to give the best fit.

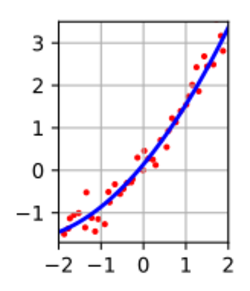
Suppose that the hypothetical researcher wishes to fit a parabola of the form [math]\displaystyle{ y = \beta_1 x^2 }[/math]. Importantly, this model is still linear in the unknown parameters (now just [math]\displaystyle{ \beta_1 }[/math]), so linear least squares still applies. The system of equations incorporating residuals is [math]\displaystyle{ \begin{alignat}{2} 6 &&\; = \beta_1 (1)^2 + r_1 \\ 5 &&\; = \beta_1 (2)^2 + r_2 \\ 7 &&\; = \beta_1 (3)^2 + r_3 \\ 10 &&\; = \beta_1 (4)^2 + r_4 \\ \end{alignat} }[/math]

The sum of squared residuals is [math]\displaystyle{ S(\beta_1) = (6 - \beta_1)^2 + (5 - 4 \beta_1)^2 + (7 - 9 \beta_1)^2 + (10 - 16 \beta_1)^2. }[/math] There is just one partial derivative to set to 0: [math]\displaystyle{ 0 = \frac{\partial S}{\partial \beta_1} = 708 \beta_1 - 498. }[/math] The solution is [math]\displaystyle{ \beta_1 = 0.703 }[/math], and the fit model is [math]\displaystyle{ y = 0.703 x^2 }[/math].

In matrix notation, the equations without residuals are again [math]\displaystyle{ \mathbf{y} = \mathbf{X} \mathbf{\beta} }[/math], where now [math]\displaystyle{ \mathbf{y} = \left[\begin{array}{c} 6 \\ 5 \\ 7 \\ 10 \end{array}\right], \;\;\;\; \mathbf{X} = \left[\begin{array}{c}1 \\ 4 \\ 9 \\ 16 \end{array}\right], \;\;\;\; \mathbf{\beta} = \left[\begin{array}{c} \beta_1 \end{array}\right]. }[/math] By the same logic as above, the solution is [math]\displaystyle{ \mathbf{\beta} = \left(\mathbf{X}^\top \mathbf{X}\right)^{-1} \mathbf{X}^\top \mathbf{y} = \left[\begin{array}{c} 0.703 \end{array}\right]. }[/math]

The figure shows an extension to fitting the three parameter parabola using a design matrix [math]\displaystyle{ \mathbf{X} }[/math] with three columns (one for [math]\displaystyle{ x^0 }[/math], [math]\displaystyle{ x^1 }[/math], and [math]\displaystyle{ x^2 }[/math]), and one row for each of the red data points.

Fitting other curves and surfaces

More generally, one can have [math]\displaystyle{ n }[/math] regressors [math]\displaystyle{ x_j }[/math], and a linear model [math]\displaystyle{ y = \beta_0 + \sum_{j=1}^{n} \beta_{j} x_{j}. }[/math]

See also

• Line-line intersection#Nearest point to non-intersecting lines, an application
• Line fitting
• Nonlinear least squares
• Regularized least squares
• Simple linear regression
• Partial least squares regression
• Linear function

Further reading

• Bevington, Philip R.; Robinson, Keith D. (2003). Data Reduction and Error Analysis for the Physical Sciences. McGraw-Hill. ISBN 978-0-07-247227-1. 

External links

• Least Squares Fitting – From MathWorld
• Least Squares Fitting-Polynomial – From MathWorld