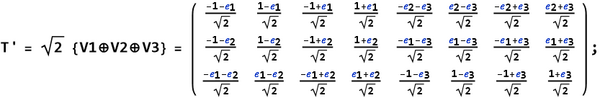Dual snub 24-cell
| Dual snub 24-cell | ||
 Orthogonal projection | ||
| Type | 4-polytope | |
| Cells | 96 
| |
| Faces | 432 | 144 kites 288 Isosceles triangle |
| Edges | 480 | |
| Vertices | 144 | |
| Dual | Snub 24-cell | |
| Properties | convex | |
In geometry, the dual snub 24-cell is a 144 vertex convex 4-polytope composed of 96 irregular cells. Each cell has faces of two kinds: 3 kites and 6 isosceles triangles.[1] The polytope has a total of 432 faces (144 kites and 288 isosceles triangles) and 480 edges.
Geometry
The dual snub 24-cell, first described by Koca et al. in 2011,[2] is the dual polytope of the snub 24-cell, a semiregular polytope first described by Thorold Gosset in 1900.[3]
Construction
The vertices of a dual snub 24-cell are obtained using quaternion simple roots (T') in the generation of the 600 vertices of the 120-cell.[4] The following describe [math]\displaystyle{ T }[/math] and [math]\displaystyle{ T' }[/math] 24-cells as quaternion orbit weights of D4 under the Weyl group W(D4):
O(0100) : T = {±1,±e1,±e2,±e3,(±1±e1±e2±e3)/2}
O(1000) : V1
O(0010) : V2
O(0001) : V3
With quaternions [math]\displaystyle{ (p,q) }[/math] where [math]\displaystyle{ \bar p }[/math] is the conjugate of [math]\displaystyle{ p }[/math] and [math]\displaystyle{ [p,q]:r\rightarrow r'=prq }[/math] and [math]\displaystyle{ [p,q]^*:r\rightarrow r''=p\bar rq }[/math], then the Coxeter group [math]\displaystyle{ W(H_4)=\lbrace[p,\bar p] \oplus [p,\bar p]^*\rbrace }[/math] is the symmetry group of the 600-cell and the 120-cell of order 14400.
Given [math]\displaystyle{ p \in T }[/math] such that [math]\displaystyle{ \bar p=\pm p^4, \bar p^2=\pm p^3, \bar p^3=\pm p^2, \bar p^4=\pm p }[/math] and [math]\displaystyle{ p^\dagger }[/math] as an exchange of [math]\displaystyle{ -1/\phi \leftrightarrow \phi }[/math] within [math]\displaystyle{ p }[/math] where [math]\displaystyle{ \phi=\frac{1+\sqrt{5}}{2} }[/math] is the golden ratio, we can construct:
- the snub 24-cell [math]\displaystyle{ S=\sum_{i=1}^4\oplus p^i T }[/math]
- the 600-cell [math]\displaystyle{ I=T+S=\sum_{i=0}^4\oplus p^i T }[/math]
- the 120-cell [math]\displaystyle{ J=\sum_{i,j=0}^4\oplus p^i\bar p^{\dagger j}T' }[/math]
- the alternate snub 24-cell [math]\displaystyle{ S'=\sum_{i=1}^4\oplus p^i\bar p^{\dagger i}T' }[/math]
and finally the dual snub 24-cell can then be defined as the orbits of [math]\displaystyle{ T \oplus T' \oplus S' }[/math].
Projections
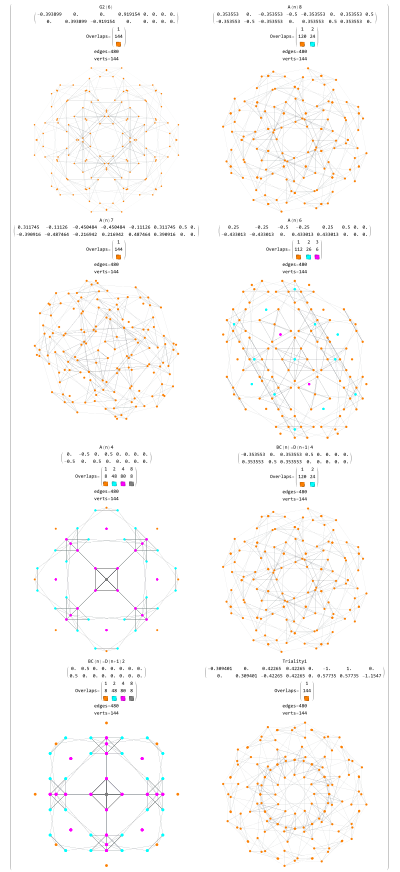
 3D overlay of the dual snub 24-cell with the orthogonal projection of the 120-cell which forms an outer hull of a unit circumradius chamfered dodecahedron. Of the 600 vertices in the 120-cell (J), 120 of the dual snub 24-cell (T'+S') are a subset of J and 24 (the T 24-cell) are not. Some of those 24 can be seen projecting outside the convex 3D hull of the 120-cell. As itemized in the hull data of this diagram, the 8 16-cell vertices of T have 6 with unit norm and can be seen projecting outside the center of 6 hexagon faces, while 2 with a [math]\displaystyle{ \pm }[/math]1 in the 4th dimension get projected to the origin in 3D. The 16 other vertices are the 8-cell Tesseract which project to norm [math]\displaystyle{ \tfrac{\sqrt{3}}{2}=.866 }[/math] inside the 120-cell 3D hull. Please note: the face and cell count data, along with the area and volume, within this image are from Mathematica automated tetrahedral cell analysis and are not based on the 96 kite cells of the dual snub 24-cell. |
Dual
The dual polytope of this polytope is the Snub 24-cell.[5]
See also
Citations
- ↑ Koca, Al-Ajmi & Ozdes Koca 2011, pp. 986-987, Fig. 4.
- ↑ Koca, Al-Ajmi & Ozdes Koca 2011.
- ↑ Gosset 1900.
- ↑ Koca, Al-Ajmi & Ozdes Koca 2011, pp. 986-988, 6. Dual of the snub 24-cell.
- ↑ Coxeter 1973, pp. 151-153, §8.4. The snub {3,4,3}.
References
- Gosset, Thorold (1900). "On the Regular and Semi-Regular Figures in Space of n Dimensions". Messenger of Mathematics (Macmillan).
- Coxeter, H.S.M. (1973). Regular Polytopes (3rd ed.). New York: Dover.
- Conway, John; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). The Symmetries of Things. ISBN 978-1-56881-220-5.
- Koca, Mehmet; Ozdes Koca, Nazife; Al-Barwani, Muataz (2012). "Snub 24-Cell Derived from the Coxeter-Weyl Group W(D4)". Int. J. Geom. Methods Mod. Phys. 09 (8). doi:10.1142/S0219887812500685. http://arxiv-web3.library.cornell.edu/abs/1106.3433.
- Koca, Mehmet; Al-Ajmi, Mudhahir; Ozdes Koca, Nazife (2011). "Quaternionic representation of snub 24-cell and its dual polytope derived from E8 root system". Linear Algebra and Its Applications 434 (4): 977–989. doi:10.1016/j.laa.2010.10.005. ISSN 0024-3795.
Fundamental convex regular and uniform polytopes in dimensions 2–10
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 |