A7 polytope
From HandWiki
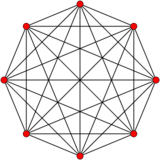 7-simplex |
In 7-dimensional geometry, there are 71 uniform polytopes with A7 symmetry. There is one self-dual regular form, the 7-simplex with 8 vertices.
Each can be visualized as symmetric orthographic projections in Coxeter planes of the A7 Coxeter group, and other subgroups.
Graphs
Symmetric orthographic projections of these 71 polytopes can be made in the A7, A6, A5, A4, A3, A2 Coxeter planes. Ak has [k+1] symmetry. For even k and symmetrically ringed-diagrams, symmetry doubles to [2(k+1)].
These 71 polytopes are each shown in these 6 symmetry planes, with vertices and edges drawn, and vertices colored by the number of overlapping vertices in each projective position.
| # | Coxeter-Dynkin diagram Schläfli symbol Johnson name |
Ak orthogonal projection graphs | |||||
|---|---|---|---|---|---|---|---|
| A7 [8] |
A6 [7] |
A5 [6] |
A4 [5] |
A3 [4] |
A2 [3] | ||
| 1 | t0{3,3,3,3,3,3} 7-simplex |
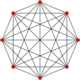
|

|
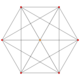
|

|

|
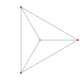
|
| 2 | t1{3,3,3,3,3,3} Rectified 7-simplex |

|

|

|

|
|

|
| 3 | t2{3,3,3,3,3,3} Birectified 7-simplex |

|

|
|

|

|
|
| 4 | t3{3,3,3,3,3,3} Trirectified 7-simplex |
|

|
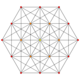
|
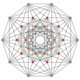
|
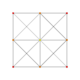
|
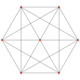
|
| 5 | t0,1{3,3,3,3,3,3} Truncated 7-simplex |

|

|
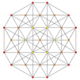
|

|
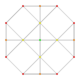
|
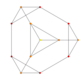
|
| 6 | t0,2{3,3,3,3,3,3} Cantellated 7-simplex |

|

|
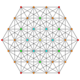
|

|
|

|
| 7 | t1,2{3,3,3,3,3,3} Bitruncated 7-simplex |

|

|
|

|

|
|
| 8 | t0,3{3,3,3,3,3,3} Runcinated 7-simplex |

|

|
|
|
|
|
| 9 | t1,3{3,3,3,3,3,3} Bicantellated 7-simplex |

|

|
|
|
|

|
| 10 | t2,3{3,3,3,3,3,3} Tritruncated 7-simplex |

|

|

|
|

|

|
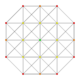
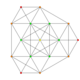
| 11 | t0,4{3,3,3,3,3,3} Stericated 7-simplex |

|

|
|

|
|
|
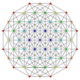
| 12 | t1,4{3,3,3,3,3,3} Biruncinated 7-simplex |
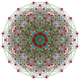
|

|
|
|

|
|
| 13 | t2,4{3,3,3,3,3,3} Tricantellated 7-simplex |

|

|
|
|
|

|
| 14 | t0,5{3,3,3,3,3,3} Pentellated 7-simplex |

|
|

|

|
|
|
| 15 | t1,5{3,3,3,3,3,3} Bistericated 7-simplex |
|

|
|
|
|
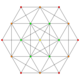
|
| 16 | t0,6{3,3,3,3,3,3} Hexicated 7-simplex |
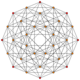
|

|
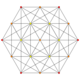
|
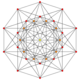
|

|

|
| 17 | t0,1,2{3,3,3,3,3,3} Cantitruncated 7-simplex |

|
|
|

|
|
|
| 18 | t0,1,3{3,3,3,3,3,3} Runcitruncated 7-simplex |

|

|
|
|
|
|
| 19 | t0,2,3{3,3,3,3,3,3} Runcicantellated 7-simplex |
|

|
|
|
|
|
| 20 | t1,2,3{3,3,3,3,3,3} Bicantitruncated 7-simplex |

|

|
|

|
|
|
| 21 | t0,1,4{3,3,3,3,3,3} Steritruncated 7-simplex |

|

|
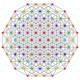
|
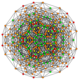
|
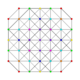
|
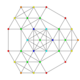
|
| 22 | t0,2,4{3,3,3,3,3,3} Stericantellated 7-simplex |

|

|
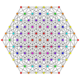
|
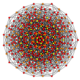
|
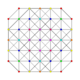
|
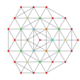
|
| 23 | t1,2,4{3,3,3,3,3,3} Biruncitruncated 7-simplex |

|

|
|
|

|
|
| 24 | t0,3,4{3,3,3,3,3,3} Steriruncinated 7-simplex |
|

|
|
|
|

|
| 25 | t1,3,4{3,3,3,3,3,3} Biruncicantellated 7-simplex |

|

|

|
|

|
|
| 26 | t2,3,4{3,3,3,3,3,3} Tricantitruncated 7-simplex |

|

|
|
|

|
|
| 27 | t0,1,5{3,3,3,3,3,3} Pentitruncated 7-simplex |

|

|
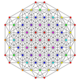
|
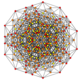
|
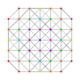
|
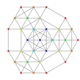
|
| 28 | t0,2,5{3,3,3,3,3,3} Penticantellated 7-simplex |

|

|
|

|
|

|
| 29 | t1,2,5{3,3,3,3,3,3} Bisteritruncated 7-simplex |

|

|
|
|

|
|
| 30 | t0,3,5{3,3,3,3,3,3} Pentiruncinated 7-simplex |

|

|
|
|
|
|
| 31 | t1,3,5{3,3,3,3,3,3} Bistericantellated 7-simplex |

|

|
|

|

|
|
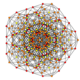
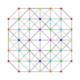
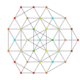
| 32 | t0,4,5{3,3,3,3,3,3} Pentistericated 7-simplex |
|

|

|
|
|
|
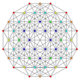
| 33 | t0,1,6{3,3,3,3,3,3} Hexitruncated 7-simplex |

|

|
|
|

|
|
| 34 | t0,2,6{3,3,3,3,3,3} Hexicantellated 7-simplex |
|

|

|

|

|
|
| 35 | t0,3,6{3,3,3,3,3,3} Hexiruncinated 7-simplex |

|

|
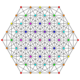
|
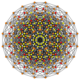
|
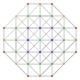
|
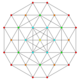
|
| 36 | t0,1,2,3{3,3,3,3,3,3} Runcicantitruncated 7-simplex |

|

|
|

|
|
|
| 37 | t0,1,2,4{3,3,3,3,3,3} Stericantitruncated 7-simplex |
|

|

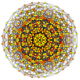
|
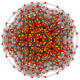
|
|

|
| 38 | t0,1,3,4{3,3,3,3,3,3} Steriruncitruncated 7-simplex |

|

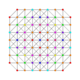
|
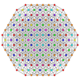
|
|
|

|
| 39 | t0,2,3,4{3,3,3,3,3,3} Steriruncicantellated 7-simplex |
|

|
|

|
|

|
| 40 | t1,2,3,4{3,3,3,3,3,3} Biruncicantitruncated 7-simplex |

|

|
|
|
|
|
| 41 | t0,1,2,5{3,3,3,3,3,3} Penticantitruncated 7-simplex |

|

|
|
|

|
|
| 42 | t0,1,3,5{3,3,3,3,3,3} Pentiruncitruncated 7-simplex |

|

|
|
|
|

|
| 43 | t0,2,3,5{3,3,3,3,3,3} Pentiruncicantellated 7-simplex |

|

|
|

|

|

|
| 44 | t1,2,3,5{3,3,3,3,3,3} Bistericantitruncated 7-simplex |

|

|
|

|
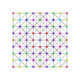
|
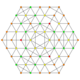
|
| 45 | t0,1,4,5{3,3,3,3,3,3} Pentisteritruncated 7-simplex |

|

|
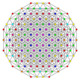
|
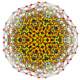
|
|

|
| 46 | t0,2,4,5{3,3,3,3,3,3} Pentistericantellated 7-simplex |

|

|
|
|
|

|
| 47 | t1,2,4,5{3,3,3,3,3,3} Bisteriruncitruncated 7-simplex |

|

|
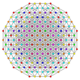
|

|
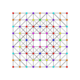
|

|
| 48 | t0,3,4,5{3,3,3,3,3,3} Pentisteriruncinated 7-simplex |

|

|

|
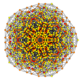
|
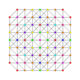
|
|
| 49 | t0,1,2,6{3,3,3,3,3,3} Hexicantitruncated 7-simplex |

|

|
|
|
|

|
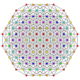
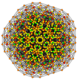
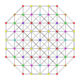
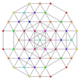
| 50 | t0,1,3,6{3,3,3,3,3,3} Hexiruncitruncated 7-simplex |

|

|
|
|
|
|
| 51 | t0,2,3,6{3,3,3,3,3,3} Hexiruncicantellated 7-simplex |

|

|
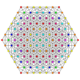
|
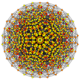
|
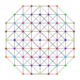
|
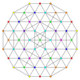
|
| 52 | t0,1,4,6{3,3,3,3,3,3} Hexisteritruncated 7-simplex |

|

|
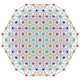
|
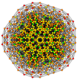
|

|
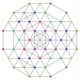
|
| 53 | t0,2,4,6{3,3,3,3,3,3} Hexistericantellated 7-simplex |

|

|
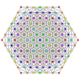
|

|
|
|
| 54 | t0,1,5,6{3,3,3,3,3,3} Hexipentitruncated 7-simplex |
|

|
|

|
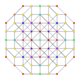
|
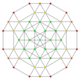
|
| 55 | t0,1,2,3,4{3,3,3,3,3,3} Steriruncicantitruncated 7-simplex |

|

|

|
|
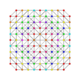
|
|
| 56 | t0,1,2,3,5{3,3,3,3,3,3} Pentiruncicantitruncated 7-simplex |

|

|
|
|
|
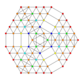
|
| 57 | t0,1,2,4,5{3,3,3,3,3,3} Pentistericantitruncated 7-simplex |

|

|

|

|

|
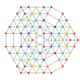
|
| 58 | t0,1,3,4,5{3,3,3,3,3,3} Pentisteriruncitruncated 7-simplex |

|

|

|
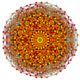
|
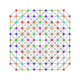
|
|
| 59 | t0,2,3,4,5{3,3,3,3,3,3} Pentisteriruncicantellated 7-simplex |

|

|

|
|
|
|
| 60 | t1,2,3,4,5{3,3,3,3,3,3} Bisteriruncicantitruncated 7-simplex |

|

|

|

|
|
|
| 61 | t0,1,2,3,6{3,3,3,3,3,3} Hexiruncicantitruncated 7-simplex |
|

|
|

|
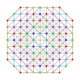
|

|
| 62 | t0,1,2,4,6{3,3,3,3,3,3} Hexistericantitruncated 7-simplex |

|

|
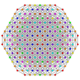
|
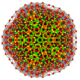
|
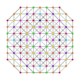
|
|
| 63 | t0,1,3,4,6{3,3,3,3,3,3} Hexisteriruncitruncated 7-simplex |

|

|
|
|
|
|
| 64 | t0,2,3,4,6{3,3,3,3,3,3} Hexisteriruncicantellated 7-simplex |
|

|

|
|
|
|
| 65 | t0,1,2,5,6{3,3,3,3,3,3} Hexipenticantitruncated 7-simplex |

|

|

|

|
|
|
| 66 | t0,1,3,5,6{3,3,3,3,3,3} Hexipentiruncitruncated 7-simplex |

|

|
|

|
|
|
| 67 | t0,1,2,3,4,5{3,3,3,3,3,3} Pentisteriruncicantitruncated 7-simplex |

|

|

|
|
|

|
| 68 | t0,1,2,3,4,6{3,3,3,3,3,3} Hexisteriruncicantitruncated 7-simplex |
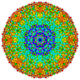
|

|

|

|
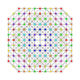
|
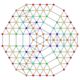
|
| 69 | t0,1,2,3,5,6{3,3,3,3,3,3} Hexipentiruncicantitruncated 7-simplex |
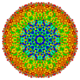
|

|

|
|
|
|
| 70 | t0,1,2,4,5,6{3,3,3,3,3,3} Hexipentistericantitruncated 7-simplex |

|

|

|

|
|
|
| 71 | t0,1,2,3,4,5,6{3,3,3,3,3,3} Omnitruncated 7-simplex |

|

|

|
|
|
|
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN:978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380–407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Klitzing, Richard. "7D uniform polytopes (polyexa)". https://bendwavy.org/klitzing/dimensions/polypeta.htm.
Notes
Fundamental convex regular and uniform polytopes in dimensions 2–10
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 |

