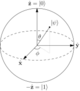
One-way quantum computer

From HandWiki
Short description: Method of quantum computing
The measurement-based techniques consist of entangling a cluster of qubits and performing a set of measurements. Thanks to the correlation between the entangled qubits, the flow of information (from left to right) is carried on by the measurements on the physical qubits in the cluster.
Part of a series on
Quantum mechanics
[math]\displaystyle{ i \hbar \frac{\partial}{\partial t} | \psi (t) \rangle = \hat{H} | \psi (t) \rangle }[/math]
Schrödinger equation
Background
Fundamentals
Effects
Experiments
Formulations
Equations
Interpretations
Advanced topics
Scientists

The one-way or measurement-based quantum computer (MBQC) is a method of quantum computing that first prepares an entangled resource state, usually a cluster state or graph state, then performs single qubit measurements on it. It is "one-way" because the resource state is destroyed by the measurements.

The outcome of each individual measurement is random, but they are related in such a way that the computation always succeeds. In general, the choices of basis for later measurements need to depend on the results of earlier measurements, and hence the measurements cannot all be performed at the same time.

The hardware implementation of MBQC mainly relies on photonic devices,[1] due to the difficulty of entangling photons without measurements, and the relative simplicity of creating and measuring them. However, MBQC is also possible with matter-based qubits.[2] The process of entanglement and measurement can be described with the help of graph tools and group theory, in particular by the elements from the stabilizer group.

Definition

The purpose of quantum computing focuses on building an information theory with the features of quantum mechanics: instead of encoding a binary unit of information (bit), which can be switched to 1 or 0, a quantum binary unit of information (qubit) can simultaneously turn to be 0 and 1 at the same time, thanks to the phenomenon called superposition.[3][4][5] Another key feature for quantum computing relies on the entanglement between the qubits.[6][7][8]

A quantum circuit implementing the Bernstein-Vazirani algorithm: [math]\displaystyle{ H }[/math] and [math]\displaystyle{ U_f }[/math] represent the logic gates (unitary operators) which act on the register of qubits. In the MBQC frame, the logic gates are performed by entangling the qubits and measuring the auxiliary ones.

In the quantum logic gate model, a set of qubits, called register, is prepared at the beginning of the computation, then a set of logic operations over the qubits, carried by unitary operators, is implemented.[9][10] A quantum circuit is formed by a register of qubits on which unitary transformations are applied over the qubits. In the measurement-based quantum computation, instead of implementing a logic operation via unitary transformations, the same operation is executed by entangling a number [math]\displaystyle{ k }[/math] of input qubits with a cluster of [math]\displaystyle{ a }[/math] ancillary qubits, forming an overall source state of [math]\displaystyle{ a+k=n }[/math] qubits, and then measuring a number [math]\displaystyle{ m }[/math] of them.[11][12] The remaining [math]\displaystyle{ k=n-a }[/math] output qubits will be affected by the measurements because of the entanglement with the measured qubits. The one-way computer has been proved to be a universal quantum computer, which means it can reproduce any unitary operation over an arbitrary number of qubits.[9][13][14][15]

General procedure

The standard process of measurement-based quantum computing consists of three steps:[16][17] entangle the qubits, measure the ancillae (auxiliary qubits) and correct the outputs. In the first step, the qubits are entangled in order to prepare the source state. In the second step, the ancillae are measured, affecting the state of the output qubits. However, the measurement outputs are non-deterministic result, due to undetermined nature of quantum mechanics:[17] in order to carry on the computation in a deterministic way, some correction operators, called byproducts, are introduced.

Preparing the source state

The CZ operation in the circuit diagrams.

At the beginning of the computation, the qubits can be distinguished into two categories: the input and the ancillary qubits. The inputs represent the qubits set in a generic [math]\displaystyle{ | \psi \rangle = \alpha |0\rangle + \beta |1 \rangle }[/math] state, on which some unitary transformations are to be acted. In order to prepare the source state, all the ancillary qubits must be prepared in the [math]\displaystyle{ |+\rangle }[/math] state:[11][18]

[math]\displaystyle{ |+\rangle = \tfrac{| 0 \rangle + | 1 \rangle}{\sqrt{2}}, }[/math]

where [math]\displaystyle{ | 0 \rangle }[/math] and [math]\displaystyle{ | 1 \rangle }[/math] are the quantum encoding for the classical [math]\displaystyle{ 0 }[/math] and [math]\displaystyle{ 1 }[/math] bits:

[math]\displaystyle{ | 0 \rangle = \begin{pmatrix} 1 \\ 0 \end{pmatrix};\quad | 1 \rangle = \begin{pmatrix} 0 \\ 1 \end{pmatrix} }[/math].

A register with [math]\displaystyle{ n }[/math] qubits will be therefore set as [math]\displaystyle{ | + \rangle^{\otimes n} }[/math]. Thereafter, the entanglement between two qubits can be performed by applying a [math]\displaystyle{ CZ }[/math] gate operation.[19] The matrix representation of such two-qubits operator is given by

[math]\displaystyle{ CZ =\begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{bmatrix}. }[/math]

The action of a [math]\displaystyle{ CZ }[/math] gate over two qubits can be described by the following system:

[math]\displaystyle{ \begin{cases} CZ | 0+ \rangle = | 0+ \rangle \\ CZ | 0- \rangle = | 0- \rangle \\ CZ | 1+ \rangle = | 1- \rangle \\ CZ | 1- \rangle = | 1+ \rangle \end{cases} }[/math]

When applying a [math]\displaystyle{ CZ }[/math] gate over two ancillae in the [math]\displaystyle{ |+ \rangle }[/math] state, the overall state

[math]\displaystyle{ CZ| ++ \rangle = \frac{| 0+ \rangle + | 1- \rangle}{\sqrt 2} }[/math]

turns to be an entangled pair of qubits. When entangling two ancillae, no importance is given about which is the control qubit and which one the target, as far as the outcome turns to be the same. Similarly, as the [math]\displaystyle{ CZ }[/math] gates are represented in a diagonal form, they all commute each other, and no importance is given about which qubits to entangle first. Photons are the most common source to prepare entangled physical qubits.[20][21][22]

Measuring the qubits

Implementation of X and Z gates over two qubits in the circuit diagrams.

The process of measurement over a single-particle state can be described by projecting the state on the eigenvector of an observable. Consider an observable [math]\displaystyle{ O }[/math] with two possible eigenvectors, say [math]\displaystyle{ | o_1 \rangle }[/math] and [math]\displaystyle{ | o_2 \rangle }[/math], and suppose to deal with a multi-particle quantum system [math]\displaystyle{ | \Psi \rangle }[/math]. Measuring the [math]\displaystyle{ i }[/math]-th qubit by the [math]\displaystyle{ O }[/math] observable means to project the [math]\displaystyle{ | \Psi \rangle }[/math] state over the eigenvectors of [math]\displaystyle{ O }[/math]:[18]

[math]\displaystyle{ | \Psi' \rangle = |o_i \rangle \langle o_i | \Psi \rangle }[/math].

The actual state of the [math]\displaystyle{ i }[/math]-th qubit is now [math]\displaystyle{ |o_i \rangle }[/math], which can turn to be [math]\displaystyle{ | o_1 \rangle }[/math] or [math]\displaystyle{ | o_2 \rangle }[/math], depending on the outcome from the measurement (which is probabilistic in quantum mechanics). The measurement projection can be performed over the eigenstates of the [math]\displaystyle{ M(\theta) = \cos(\theta)X + \sin(\theta)Y }[/math] observable:

[math]\displaystyle{ M(\theta) = \cos(\theta) \begin{bmatrix} 0 & 1 \\ 1 & 0 \end{bmatrix} + \sin(\theta) \begin{bmatrix} 0 & -i \\ i & 0 \end{bmatrix} = \begin{bmatrix} 0 & e^{-i \theta} \\ e^{i \theta} & 0 \end{bmatrix} }[/math],

where [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Y }[/math] belong to the Pauli matrices. The eigenvectors of [math]\displaystyle{ M(\theta) }[/math] are [math]\displaystyle{ |\theta_\pm \rangle = |0 \rangle \pm e^{i \theta} |1 \rangle }[/math]. Measuring a qubit on the [math]\displaystyle{ X }[/math]-[math]\displaystyle{ Y }[/math] plane, i.e. by the [math]\displaystyle{ M(\theta) }[/math] observable, means to project it over [math]\displaystyle{ |\theta_+ \rangle }[/math] or [math]\displaystyle{ |\theta_- \rangle }[/math]. In the one-way quantum computing, once a qubit has been measured, there is no way to recycle it in the flow of computation. Therefore, instead of using the [math]\displaystyle{ |o_i \rangle \langle o_i | }[/math] notation, it is common to find [math]\displaystyle{ \langle o_i | }[/math] to indicate a projective measurement over the [math]\displaystyle{ i }[/math]-th qubit.

Correcting the output

After all the measurements have been performed, the system has been reduced to a smaller number of qubits, which form the output state of the system. Due to the probabilistic outcome of measurements, the system is not set in a deterministic way: after a measurement on the [math]\displaystyle{ X }[/math]-[math]\displaystyle{ Y }[/math] plane, the output may change whether the outcome had been [math]\displaystyle{ | \theta_+ \rangle }[/math] or [math]\displaystyle{ | \theta_- \rangle }[/math]. In order to perform a deterministic computation, some corrections must be introduced. The correction operators, or byproduct operators, are applied to the output qubits after all the measurements have been performed.[18][23] The byproduct operators which can be implemented are [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math].[24] Depending on the outcome of the measurement, a byproduct operator can be applied or not to the output state: a [math]\displaystyle{ X }[/math] correction over the [math]\displaystyle{ j }[/math]-th qubit, depending on the outcome of the measurement performed over the [math]\displaystyle{ i }[/math]-th qubit via the [math]\displaystyle{ M(\theta) }[/math] observable, can be described as [math]\displaystyle{ X_j^{s_i} }[/math], where [math]\displaystyle{ s_i }[/math] is set to be [math]\displaystyle{ 0 }[/math] if the outcome of measurement was [math]\displaystyle{ | \theta_+ \rangle }[/math], otherwise is [math]\displaystyle{ 1 }[/math] if it was [math]\displaystyle{ | \theta_- \rangle }[/math]. In the first case, no correction will occur, in the latter one a [math]\displaystyle{ X }[/math] operator will be implemented on the [math]\displaystyle{ j }[/math]-th qubit. Eventually, even though the outcome of a measurement is not deterministic in quantum mechanics, the results from measurements can be used in order to perform corrections, and carry on a deterministic computation.

CME pattern

The Euler rotation (with respect to the XZX basis) in the MBQC computation. The lines describe the entanglement between the qubits. The first qubit corresponds to the input state [math]\displaystyle{ | \psi \rangle }[/math], the fifth one to the output state. The qubits from 2 to 4 are the ancillae. All the states, except for the input, are prepared in the [math]\displaystyle{ | + \rangle }[/math] state. All the qubits, except for the output, are measured by the [math]\displaystyle{ M }[/math] observable with a specific angle. After the measurements have been carried on, implementing the [math]\displaystyle{ U }[/math] unitary, the [math]\displaystyle{ X }[/math] and [math]\displaystyle{ Z }[/math] corrections are performed with respect to the [math]\displaystyle{ s_i }[/math] outcomes.

The operations of entanglement, measurement and correction can be performed in order to implement unitary gates. Such operations can be performed time by time for any logic gate in the circuit, or rather in a pattern which allocates all the entanglement operations at the beginning, the measurements in the middle and the corrections at the end of the circuit. Such pattern of computation is referred to as CME standard pattern.[16][17] In the CME formalism, the operation of entanglement between the [math]\displaystyle{ i }[/math] and [math]\displaystyle{ j }[/math] qubits is referred to as [math]\displaystyle{ E_{ij} }[/math]. The measurement on the [math]\displaystyle{ i }[/math] qubit, in the [math]\displaystyle{ X }[/math]-[math]\displaystyle{ Y }[/math] plane, with respect to a [math]\displaystyle{ \theta }[/math] angle, is defined as [math]\displaystyle{ M_i^\theta }[/math]. At last, the [math]\displaystyle{ X }[/math] byproduct over a [math]\displaystyle{ i }[/math] qubit, with respect to the measurement over a [math]\displaystyle{ j }[/math] qubit, is described as [math]\displaystyle{ X_i^{s_j} }[/math], where [math]\displaystyle{ s_j }[/math] is set to [math]\displaystyle{ 0 }[/math] if the outcome is the [math]\displaystyle{ | \theta_+ \rangle }[/math] state, [math]\displaystyle{ 1 }[/math] when the outcome is [math]\displaystyle{ | \theta_- \rangle }[/math]. The same notation holds for the [math]\displaystyle{ Z }[/math] byproducts.

When performing a computation following the CME pattern, it may happen that two measurements [math]\displaystyle{ M_i^{\theta_1} }[/math] and [math]\displaystyle{ M_j^{\theta_2} }[/math] on the [math]\displaystyle{ X }[/math]-[math]\displaystyle{ Y }[/math] plane depend one on the outcome from the other. For example, the sign in front of the angle of measurement on the [math]\displaystyle{ j }[/math]-th qubit can be flipped with respect to the measurement over the [math]\displaystyle{ i }[/math]-th qubit: in such case, the notation will be written as [math]\displaystyle{ [M_j^{\theta_2}]^{s_i} M_i^{\theta_1} }[/math], and therefore the two operations of measurement do commute each other no more. If [math]\displaystyle{ s_i }[/math] is set to [math]\displaystyle{ 0 }[/math], no flip on the [math]\displaystyle{ \theta_2 }[/math] sign will occur, otherwise (when [math]\displaystyle{ s_i=1 }[/math]) the [math]\displaystyle{ \theta_2 }[/math] angle will be flipped to [math]\displaystyle{ -\theta_2 }[/math]. The notation [math]\displaystyle{ [M_j^{\theta_2}]^{s_i} }[/math] can therefore be rewritten as [math]\displaystyle{ M_j^{(-)^{s_i}\theta_2} }[/math].

An example: Euler rotations

As an illustrative example, consider the Euler rotation in the [math]\displaystyle{ XZX }[/math] basis: such operation, in the gate model of quantum computation, is described as[25]

[math]\displaystyle{ e^{i \gamma}R_X(\phi) R_Z(\theta)R_X(\lambda) }[/math],

where [math]\displaystyle{ \phi, \theta, \lambda }[/math] are the angles for the rotation, while [math]\displaystyle{ \gamma }[/math] defines a global phase which is irrelevant for the computation. To perform such operation in the one-way computing frame, it is possible to implement the following CME pattern:[23][26]

[math]\displaystyle{ Z_5^{s_1+s_3}X_5^{s_2+s_4} [M_4^{-\phi}]^{s_1+s_3} [M_3^{-\theta}]^{s_2} [M_2^{-\lambda}]^{s_1} M_1^{0} E_{4,5} E_{3,4} E_{2,3} E_{1,2} }[/math],

where the input state [math]\displaystyle{ | \psi \rangle = \alpha | 0 \rangle + \beta | 1 \rangle }[/math] is the qubit [math]\displaystyle{ 1 }[/math], all the other qubits are auxiliary ancillae and therefore have to be prepared in the [math]\displaystyle{ | + \rangle }[/math] state. In the first step, the input state [math]\displaystyle{ |\psi \rangle }[/math] must be entangled with the second qubits; in turn, the second qubit must be entangled with the third one and so on. The entangling operations [math]\displaystyle{ E_{ij} }[/math] between the qubits can be performed by the [math]\displaystyle{ CZ }[/math] gates.

In the second place, the first and the second qubits must be measured by the [math]\displaystyle{ M(\theta) }[/math] observable, which means they must be projected onto the eigenstates [math]\displaystyle{ | \theta \rangle }[/math] of such observable. When the [math]\displaystyle{ \theta }[/math] is zero, the [math]\displaystyle{ | \theta_\pm \rangle }[/math] states reduce to [math]\displaystyle{ |\pm \rangle }[/math] ones, i.e. the eigenvectors for the [math]\displaystyle{ X }[/math] Pauli operator. The first measurement [math]\displaystyle{ M_1^{0} }[/math] is performed on the qubit [math]\displaystyle{ 1 }[/math] with a [math]\displaystyle{ \theta=0 }[/math] angle, which means it has to be projected onto the [math]\displaystyle{ \langle \pm | }[/math] states. The second measurement [math]\displaystyle{ [M_2^{-\lambda}]^{s_1} }[/math] is performed with respect to the [math]\displaystyle{ -\lambda }[/math] angle, i.e. the second qubit has to be projected on the [math]\displaystyle{ \langle 0 | \pm e^{i \lambda} \langle 1 | }[/math] state. However, if the outcome from the previous measurement has been [math]\displaystyle{ \langle - | }[/math], the sign of the [math]\displaystyle{ \lambda }[/math] angle has to be flipped, and the second qubit will be projected to the [math]\displaystyle{ \langle 0 | + e^{-i \lambda} \langle 1 | }[/math] state; if the outcome from the first measurement has been [math]\displaystyle{ \langle + | }[/math], no flip needs to be performed. The same operations have to be repeated for the third [math]\displaystyle{ [M_3^{\theta}]^{s_2} }[/math] and the fourth [math]\displaystyle{ [M_4^{\phi}]^{s_1+s_3} }[/math] measurements, according to the respective angles and sign flips. The sign over the [math]\displaystyle{ \phi }[/math] angle is set to be [math]\displaystyle{ (-)^{s_1+s_3} }[/math]. Eventually the fifth qubit (the only one not to be measured) figures out to be the output state.

At last, the corrections [math]\displaystyle{ Z_5^{s_1+s_3}X_5^{s_2+s_4} }[/math] over the output state have to be performed via the byproduct operators. For instance, if the measurements over the second and the fourth qubits turned to be [math]\displaystyle{ \langle \phi_+ | }[/math] and [math]\displaystyle{ \langle \lambda_+ | }[/math], no correction will be conducted by the [math]\displaystyle{ X_5 }[/math] operator, as [math]\displaystyle{ s_2=s_4=0 }[/math]. The same result holds for a [math]\displaystyle{ \langle \phi_- | }[/math] [math]\displaystyle{ \langle \lambda_- | }[/math] outcome, as [math]\displaystyle{ s_2=s_4=1 }[/math] and thus the squared Pauli operator [math]\displaystyle{ X^2 }[/math] returns the identity.

As seen in such example, in the measurement-based computation model, the physical input qubit (the first one) and output qubit (the third one) may differ each other.

Equivalence between quantum circuit model and MBQC

The one-way quantum computer allows the implementation of a circuit of unitary transformations through the operations of entanglement and measurement. At the same time, any quantum circuit can be in turn converted into a CME pattern: a technique to translate quantum circuits into a MBQC pattern of measurements has been formulated by V. Danos et al.[16][17][27]

Such conversion can be carried on by using a universal set of logic gates composed by the [math]\displaystyle{ CZ }[/math] and the [math]\displaystyle{ J(\theta) }[/math] operators: therefore, any circuit can be decomposed into a set of [math]\displaystyle{ CZ }[/math] and the [math]\displaystyle{ J(\theta) }[/math] gates. The [math]\displaystyle{ J(\theta) }[/math] single-qubit operator is defined as follows:

[math]\displaystyle{ J(\theta) = \frac{1}{\sqrt 2} \begin{pmatrix} 1 & e^{i \theta} \\ 1 & -e^{i\theta} \end{pmatrix} }[/math].

The [math]\displaystyle{ J(\theta) }[/math] can be converted into a CME pattern as follows:

[math]\displaystyle{ J(\theta) = X_2 M_1^{-\theta} E_{1,2} }[/math]

which means, to implement a [math]\displaystyle{ J(\theta) }[/math] operator, the input qubits [math]\displaystyle{ | \psi \rangle }[/math] must be entangled with an ancilla qubit [math]\displaystyle{ | + \rangle }[/math], therefore the input must be measured on the [math]\displaystyle{ X }[/math]-[math]\displaystyle{ Y }[/math] plane, thereafter the output qubit is corrected by the [math]\displaystyle{ X_2 }[/math] byproduct. Once every [math]\displaystyle{ J(\theta) }[/math] gate has been decomposed into the CME pattern, the operations in the overall computation will consist of [math]\displaystyle{ E_{ij} }[/math] entanglements, [math]\displaystyle{ M_i^{-\theta_i} }[/math] measurements and [math]\displaystyle{ X_j }[/math] corrections. In order to lead the whole flow of computation to a CME pattern, some rules are provided.

Standardization

In order to move all the [math]\displaystyle{ E_{ij} }[/math] entanglements at the beginning of the process, some rules of commutation must be pointed out:

[math]\displaystyle{ E_{ij} Z_i^s = Z_i^s E_{ij} }[/math]
[math]\displaystyle{ E_{ij} X_i^s = X_i^s Z_j^s E_{ij} }[/math]
[math]\displaystyle{ E_{ij} A_k = A_k E_{ij} }[/math].

The entanglement operator [math]\displaystyle{ E_{ij} }[/math] commutes with the [math]\displaystyle{ Z }[/math] Pauli operators and with any other operator [math]\displaystyle{ A_k }[/math] acting on a qubit [math]\displaystyle{ k\neq i,j }[/math], but not with the [math]\displaystyle{ X }[/math] Pauli operators acting on the [math]\displaystyle{ i }[/math]-th or [math]\displaystyle{ j }[/math]-th qubits.

Pauli simplification

The measurement operations [math]\displaystyle{ M_i^\theta }[/math] commute with the corrections in the following manner:

[math]\displaystyle{ M_i^\theta X_i^s = [M_i^\theta]^s }[/math]
[math]\displaystyle{ M_i^\theta Z_i^t = S_i^t M_i^\theta }[/math],

where [math]\displaystyle{ [M_i^\theta]^s=M_i^{(-)^s\theta} }[/math]. Such operation means that, when shifting the [math]\displaystyle{ X }[/math] corrections at the end of the pattern, some dependencies between the measurements may occur. The [math]\displaystyle{ S_i^t }[/math] operator is called signal shifting, whose action will be explained in the next paragraph. For particular [math]\displaystyle{ \theta }[/math] angles, some simplifications, called Pauli simplifications, can be introduced:

[math]\displaystyle{ M_i^0 X_i^s = M_i^0 }[/math]
[math]\displaystyle{ M_i^{\pi/2} X_i^s = M_i^{\pi/2} Z_i^s }[/math].

Signal shifting

The action of the signal shifting operator [math]\displaystyle{ S_i^t }[/math] can be explained through its rules of commutation:

[math]\displaystyle{ X_i^{s} S_i^t = S_i^t X_i^{s[(s_i+t)/s_i]} }[/math]
[math]\displaystyle{ Z_i^{s} S_i^t = S_i^t Z_i^{s[(s_i+t)/s_i]} }[/math].

The [math]\displaystyle{ s[(t+s_i)/s_i] }[/math] operation has to be explained: suppose to have a sequence of signals [math]\displaystyle{ s }[/math], consisting of [math]\displaystyle{ s_1 + s_2 + ... + s_i + ... }[/math], the operation [math]\displaystyle{ s[(t+s_i)/s_i] }[/math] means to substitute [math]\displaystyle{ s_i }[/math] with [math]\displaystyle{ s_i+t }[/math] in the sequence [math]\displaystyle{ s }[/math], which becomes [math]\displaystyle{ s_1 + s_2 + ... + s_i + t + ... }[/math]. If no [math]\displaystyle{ s_i }[/math] appears in the [math]\displaystyle{ s }[/math] sequence, no substitution will occur. To perform a correct CME pattern, every signal shifting operator [math]\displaystyle{ S_i^t }[/math] must be translated at the end of the pattern.

Stabilizer formalism

Algebraic structure → Group theory
Group theory
Cyclic group.svg
Basic notions
Group homomorphisms
Finite groups
Classification of finite simple groups
Modular groups
  • PSL(2,Z)
  • SL(2,Z)
Topological and Lie groups
Infinite dimensional Lie group
  • O(∞)
  • SU(∞)
  • Sp(∞)
Algebraic groups

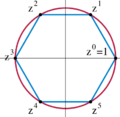When preparing the source state of entangled qubits, a graph representation can be given by the stabilizer group. The stabilizer group [math]\displaystyle{ \mathcal{S}_n }[/math] is an abelian subgroup from the Pauli group [math]\displaystyle{ \mathcal{P}_n }[/math], which one can be described by its generators [math]\displaystyle{ \{\pm 1, \pm i\} \times \{I,X,Y,Z\}^{\otimes n} }[/math].[28][29] A stabilizer state is a [math]\displaystyle{ n }[/math]-qubit state [math]\displaystyle{ | \Psi \rangle }[/math] which is a unique eigenstate for the generators [math]\displaystyle{ S_i }[/math] of the [math]\displaystyle{ \mathcal{S}_n }[/math] stabilizer group:[19]

[math]\displaystyle{ S_i | \Psi \rangle = | \Psi \rangle. }[/math]

Of course, [math]\displaystyle{ S_i \in \mathcal{S}_n \, \forall i }[/math].

A math graph defined by three vertices and three edges. Each vertex is connected with the other ones by an edge. In the MBQC frame, the vertices [math]\displaystyle{ 1,2,3 }[/math] represent the qubits, while the links between them the entanglements. In the stabilizer formalism, such graph is represented by the [math]\displaystyle{ \langle X_1 Z_2 Z_3, Z_1 X_2 Z_3, Z_1 Z_2 X_3 \rangle }[/math] generators, which all of them commute each other with.

It is therefore possible to define a [math]\displaystyle{ n }[/math] qubit graph state [math]\displaystyle{ | G \rangle }[/math] as a quantum state associated with a graph, i.e. a set [math]\displaystyle{ G=(V,E) }[/math] whose vertices [math]\displaystyle{ V }[/math] correspond to the qubits, while the edges [math]\displaystyle{ E }[/math] represent the entanglements between the qubits themselves. The vertices can be labelled by a [math]\displaystyle{ i }[/math] index, while the edges, linking the [math]\displaystyle{ i }[/math]-th vertex to the [math]\displaystyle{ j }[/math]-th one, by two-indices labels, such as [math]\displaystyle{ (i,j) }[/math].[30] In the stabilizer formalism, such graph structure can be encoded by the [math]\displaystyle{ K_i }[/math] generators of [math]\displaystyle{ \mathcal{S}_n }[/math], defined as[15][31][32]

[math]\displaystyle{ K_i = X_i \prod_{j \in (i,j)} Z_j }[/math],

where [math]\displaystyle{ {j \in (i,j)} }[/math] stands for all the [math]\displaystyle{ j }[/math] qubits neighboring with the [math]\displaystyle{ i }[/math]-th one, i.e. the [math]\displaystyle{ j }[/math] vertices linked by a [math]\displaystyle{ (i,j) }[/math] edge with the [math]\displaystyle{ i }[/math] vertex. Each [math]\displaystyle{ K_i }[/math] generator commute with all the others. A graph composed by [math]\displaystyle{ n }[/math] vertices can be described by [math]\displaystyle{ n }[/math] generators from the stabilizer group:

[math]\displaystyle{ \langle K_1, K_2, ..., K_n\rangle }[/math].

While the number of [math]\displaystyle{ X_i }[/math] is fixed for each [math]\displaystyle{ K_i }[/math] generator, the number of [math]\displaystyle{ Z_j }[/math] may differ, with respect to the connections implemented by the edges in the graph.

The Clifford group

The Clifford group [math]\displaystyle{ \mathcal{C}_n }[/math] is composed by elements which leave invariant the elements from the Pauli's group [math]\displaystyle{ \mathcal{P}_n }[/math]:[19][29][33]

[math]\displaystyle{ \mathcal{C}_n = \{ U \in SU(2^n) \; | \; U S U^\dagger \in \mathcal{P}_n, S \in \mathcal{P}_n \} }[/math].

The Clifford group requires three generators, which can be chosen as the Hadamard gate [math]\displaystyle{ H }[/math] and the phase rotation [math]\displaystyle{ S }[/math] for the single-qubit gates, and another two-qubits gate from the [math]\displaystyle{ CNOT }[/math] (controlled NOT gate) or the [math]\displaystyle{ CZ }[/math] (controlled phase gate):

[math]\displaystyle{ H = \frac{1}{\sqrt 2} \begin{bmatrix} 1 & 1 \\ 1 & -1 \end{bmatrix}, \quad S = \begin{bmatrix} 1 & 0 \\ 0 & i \end{bmatrix}, \quad CNOT = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{bmatrix} }[/math].

Consider a state [math]\displaystyle{ | G \rangle }[/math] which is stabilized by a set of stabilizers [math]\displaystyle{ S_i }[/math]. Acting via an element [math]\displaystyle{ U }[/math] from the Clifford group on such state, the following equalities hold:[29][34]

[math]\displaystyle{ U|G\rangle = U S_i |G\rangle = U S_i U^\dagger U |G\rangle = S'_i U |G\rangle }[/math].

Therefore, the [math]\displaystyle{ U }[/math] operations map the [math]\displaystyle{ |G\rangle }[/math] state to [math]\displaystyle{ U |G\rangle }[/math] and its [math]\displaystyle{ S_i }[/math] stabilizers to [math]\displaystyle{ U S_i U^\dagger }[/math]. Such operation may give rise to different representations for the [math]\displaystyle{ K_i }[/math] generators of the stabilizer group.

The Gottesman–Knill theorem states that, given a set of logic gates from the Clifford group, followed by [math]\displaystyle{ Z }[/math] measurements, such computation can be efficiently simulated on a classical computer in the strong sense, i.e. a computation which elaborates in a polynomial-time the probability [math]\displaystyle{ P(x) }[/math] for a given output [math]\displaystyle{ x }[/math] from the circuit.[19][29][35][36][37]

Hardware and applications

Topological cluster state quantum computer

Measurement-based computation on a periodic 3D lattice cluster state can be used to implement topological quantum error correction.[38] Topological cluster state computation is closely related to Kitaev's toric code, as the 3D topological cluster state can be constructed and measured over time by a repeated sequence of gates on a 2D array.[39]

Implementations

One-way quantum computation has been demonstrated by running the 2 qubit Grover's algorithm on a 2x2 cluster state of photons.[40][41] A linear optics quantum computer based on one-way computation has been proposed.[42]

Cluster states have also been created in optical lattices,[43] but were not used for computation as the atom qubits were too close together to measure individually.

AKLT state as a resource

It has been shown that the (spin [math]\displaystyle{ \tfrac{3}{2} }[/math]) AKLT state on a 2D honeycomb lattice can be used as a resource for MBQC.[44][45] More recently it has been shown that a spin-mixture AKLT state can be used as a resource.[46]

See also


References

  1. ↑ Fowler, Austin G.; Goyal, Kovid (2009-02-25). "Topological cluster state quantum computing". Quantum Information & Computation 9 (9&10): 721–738. doi:10.26421/QIC9.9-10-1. https://dl.acm.org/doi/10.5555/2011804.2011805. 
  2. ↑ Raussendorf, R; Harrington, J; Goyal, K (2007-06-29). "Topological fault-tolerance in cluster state quantum computation". New Journal of Physics 9 (6): 199. doi:10.1088/1367-2630/9/6/199. ISSN 1367-2630. Bibcode: 2007NJPh....9..199R. https://iopscience.iop.org/article/10.1088/1367-2630/9/6/199. 
  3. ↑ S. S. Li; G. L. Long; F. S. Bai; S. L. Feng; H. Z. Zheng (2001). "Quantum computing". Proceedings of the National Academy of Sciences 98 (21): 11847–11848. doi:10.1073/pnas.191373698. PMID 11562459. Bibcode: 2001PNAS...9811847L. 
  4. ↑ E. Grumbling; M. Horowitz (2019). Quantum computing: progress and prospects.. National Academies of Sciences, Engineering, and Medicine.. p. 2. doi:10.17226/25196. ISBN 978-0-309-47969-1. 
  5. ↑ T. Sleator; H. Weinfurter (1995). "Realizable Universal Quantum Logic Gates". Physical Review Letters 74 (20): 4087–4090. doi:10.1103/PhysRevLett.74.4087. PMID 10058409. Bibcode: 1995PhRvL..74.4087S. 
  6. ↑ T. Hey (1999). "Quantum computing: An introduction". Computing & Control Engineering Journal 10 (3): 105–112. doi:10.1049/cce:19990303. 
  7. ↑ P. Shor (1998). Quantum Computing. Documenta Mathematica. p. 468. http://nozdr.ru/data/media/biblio/kolxoz/M/ICM-1998,%20Berlin.%20Proceedings,%20Vol.%201%20Plenary%20lectures%20(no%20p.%2023-52)%20(Documenta%20Mathematica,%201998)(660s)_M_.pdf#page=434. 
  8. ↑ G.K. Brennen; C.M. Caves; P.S. Jessen; I.H. Deutsch (1999). "Quantum Logic Gates in Optical Lattices". Physical Review Letters 82 (5): 1060–1063. doi:10.1103/PhysRevLett.82.1060. Bibcode: 1999PhRvL..82.1060B. 
  9. ↑ 9.0 9.1 A. Barenco; C.H. Bennett; R. Cleve; D.P. DiVincenzo; N. Margolus; P. Shor; T. Sleator; J. Smolin et al. (1995). "Elementary gates for quantum computation". Physical Review A 74 (20): 3457–3467. doi:10.1103/PhysRevA.52.3457. PMID 9912645. Bibcode: 1995PhRvA..52.3457B. 
  10. ↑ S. Lloyd (1995). "Almost Any Quantum Logic Gate is Universal". Physical Review Letters 75 (2): 346–349. doi:10.1103/PhysRevLett.75.346. PMID 10059671. Bibcode: 1995PhRvL..75..346L. 
  11. ↑ 11.0 11.1 J. Joo; C.W. Lee; S. Kono; J. Kim (2019). "Logical measurement-based quantum computation in circuit-QED". Scientific Reports 9 (1): 16592. doi:10.1038/s41598-019-52866-3. PMID 31719588. Bibcode: 2019NatSR...916592J. 
  12. ↑ M.S. Tame; R. Prevedel; M. Paternostro; P. Bohi; M.S. Kim; A. Zeilinger (2007). "Experimental realization of Deutsch's algorithm in a one-way quantum computer.". Physical Review Letters 98 (14): 140501. doi:10.1103/PhysRevLett.98.140501. PMID 17501253. Bibcode: 2007PhRvL..98n0501T. 
  13. ↑ R. Raussendorf; D. E. Browne; H. J. Briegel (2003). "Measurement-based quantum computation with cluster states". Physical Review A 68 (2): 022312. doi:10.1103/PhysRevA.68.022312. Bibcode: 2003PhRvA..68b2312R. 
  14. ↑ P. Walther; K. J. Resch; T. Rudolph; E. Schenck; H. Weinfurter; V. Vedral; M. Aspelmeyer; A. Zeilinger (2005). "Experimental one-way quantum computing.". Nature 434 (7030): 169–176. doi:10.1038/nature03347. PMID 15758991. Bibcode: 2005Natur.434..169W. 
  15. ↑ 15.0 15.1 R. Raussendorf; H. J. Briegel (2006). "A One-Way Quantum Computer". Physical Review Letters 86 (22): 5188–91. doi:10.1103/PhysRevLett.86.5188. PMID 11384453. Bibcode: 2001PhRvL..86.5188R. 
  16. ↑ 16.0 16.1 16.2 V. Danos; E. Kashefi; P. Panangaden (2007). "The measurement calculus". Journal of the ACM 54 (2): 8. doi:10.1145/1219092.1219096. 
  17. ↑ 17.0 17.1 17.2 17.3 E. Pius (2010). Automatic Parallelisation of Quantum Circuits Using the Measurement Based Quantum Computing Model. https://static.epcc.ed.ac.uk/dissertations/hpc-msc/2009-2010/Einar%20Pius.pdf. 
  18. ↑ 18.0 18.1 18.2 A. Mantri; T.F. Demarie; J.F. Fitzsimons (2017). "Universality of quantum computation with cluster states and (X, Y)-plane measurements". Scientific Reports 7 (1): 42861. doi:10.1038/srep42861. PMID 28216652. Bibcode: 2017NatSR...742861M. 
  19. ↑ 19.0 19.1 19.2 19.3 S. Anders; H.J. Briegel (2006). "Fast simulation of stabilizer circuits using a graph state representation". Physical Review A 73 (2): 022334. doi:10.1103/PhysRevA.73.022334. Bibcode: 2006PhRvA..73b2334A. 
  20. ↑ T. Nutz; A. Milne; P. Shadbolt; T. Rudolph (2017). "Proposal for demonstration of long-range cluster state entanglement in the presence of photon loss". APL Photonics 2 (6): 066103. doi:10.1063/1.4983822. Bibcode: 2017APLP....2f6103N. 
  21. ↑ M. Gimeno-Segovia; P. Shadbolt; D.E. Browne; T. Rudolph (2015). "From Three-Photon Greenberger-Horne-Zeilinger States to Ballistic Universal Quantum Computation". Physical Review Letters 115 (2): 020502. doi:10.1103/PhysRevLett.115.020502. PMID 26207455. Bibcode: 2015PhRvL.115b0502G. 
  22. ↑ J.R. Scott; K.C. Balram (2022). "Timing Constraints Imposed by Classical Digital Control Systems on Photonic Implementations of Measurement-Based Quantum Computing". IEEE Transactions on Quantum Engineering 3: 1–20. doi:10.1109/TQE.2022.3175587. 
  23. ↑ 23.0 23.1 R. Jozsa (2006). "An introduction to measurement based quantum computation". NATO Science Series, III: Computer and Systems Sciences. Quantum Information Processing-From Theory to Experiment 199. 
  24. ↑ R. Raussendorf; H. J. Briegel (2002). "Computational model underlying the one-way quantum computer". arXiv:quant-ph/0108067.
  25. ↑ "OneQubitEulerDecomposer". https://qiskit.org/documentation/stubs/qiskit.quantum_info.OneQubitEulerDecomposer.html. 
  26. ↑ "MBQC Quick Start Guide". https://qml.baidu.com/tutorials/measurement-based-quantum-computation/mbqc-quick-start-guide.html. 
  27. ↑ "Measurement-Based Quantum Computation Module". https://qml.baidu.com/tutorials/measurement-based-quantum-computation/measurement-based-quantum-computation-module.html. 
  28. ↑ K. Fujii (2015). Quantum Computation with Topological Codes: from qubit to topological fault-tolerance. Springer. p. 28. ISBN 978-981-287-996-7. 
  29. ↑ 29.0 29.1 29.2 29.3 D. Gottesman (1998). The Heisenberg Representation of Quantum Computers. Bibcode: 1998quant.ph..7006G. 
  30. ↑ M. Hein; W. Dur; J. Eisert; R. Raussendorf; M. Van den Nest; H. Jurgen Briegel (2006). "Entanglement in Graph States and its Applications". arXiv:quant-ph/0602096.
  31. ↑ R. Raussendorf; J. Harrington; K. Goyal (2006). "A fault-tolerant one-way quantum computer.". Annals of Physics 321 (9): 2242–2270. doi:10.1016/j.aop.2006.01.012. Bibcode: 2006AnPhy.321.2242R. 
  32. ↑ M. Rossi; M. Huber; D. Bruß; C. Macchiavello (2013). "Quantum Hypergraph States". New Journal of Physics 15 (11): 113022. doi:10.1088/1367-2630/15/11/113022. Bibcode: 2013NJPh...15k3022R. 
  33. ↑ M.E. Cuffaro (2013). "On the Significance of the Gottesman–Knill Theorem". The British Journal for the Philosophy of Science 68 (1): 91–121. doi:10.1093/bjps/axv016. 
  34. ↑ K. Fujii (2015). Quantum Computation with Topological Codes: from qubit to topological fault-tolerance.. Springer. p. 30. ISBN 978-981-287-996-7. 
  35. ↑ K. Fujii (2015). Quantum Computation with Topological Codes: from qubit to topological fault-tolerance.. Springer. p. 34. ISBN 978-981-287-996-7. 
  36. ↑ M.A. Nielsen; I.L. Chuang (2000). Quantum Computation and Quantum Information. Cambridge University Press. p. 464. ISBN 978-1-107-00217-3. 
  37. ↑ M. Van den Nest (2008). "Classical simulation of quantum computation, the Gottesman-Knill theorem, and slightly beyond". Quantum Information & Computation 10 (3). 
  38. ↑ Robert Raussendorf; Jim Harrington; Kovid Goyal (2007). "Topological fault-tolerance in cluster state quantum computation". New Journal of Physics 9 (6): 199. doi:10.1088/1367-2630/9/6/199. Bibcode: 2007NJPh....9..199R. 
  39. ↑ Robert Raussendorf; Jim Harrington (2007). "Fault-tolerant quantum computation with high threshold in two dimensions". Physical Review Letters 98 (19): 190504. doi:10.1103/physrevlett.98.190504. PMID 17677613. Bibcode: 2007PhRvL..98s0504R. 
  40. ↑ P. Walther, K. J. Resch, T. Rudolph, E. Schenck, H. Weinfurter, V. Vedral, M. Aspelmeyer and A. Zeilinger (2005). "Experimental one-way quantum computing". Nature 434 (7030): 169–76. doi:10.1038/nature03347. PMID 15758991. Bibcode: 2005Natur.434..169W. 
  41. ↑ Robert Prevedel; Philip Walther; Felix Tiefenbacher; Pascal Böhi; Rainer Kaltenbaek; Thomas Jennewein; Anton Zeilinger (2007). "High-speed linear optics quantum computing using active feed-forward". Nature 445 (7123): 65–69. doi:10.1038/nature05346. PMID 17203057. Bibcode: 2007Natur.445...65P. 
  42. ↑ Daniel E. Browne; Terry Rudolph (2005). "Resource-efficient linear optical quantum computation". Physical Review Letters 95 (1): 010501. doi:10.1103/PhysRevLett.95.010501. PMID 16090595. Bibcode: 2005PhRvL..95a0501B. 
  43. ↑ Olaf Mandel; Markus Greiner; Artur Widera; Tim Rom; Theodor W. Hänsch; Immanuel Bloch (2003). "Controlled collisions for multi-particle entanglement of optically trapped atoms". Nature 425 (6961): 937–40. doi:10.1038/nature02008. PMID 14586463. Bibcode: 2003Natur.425..937M. 
  44. ↑ Tzu-Chieh Wei; Ian Affleck; Robert Raussendorf (2012). "Two-dimensional Affleck-Kennedy-Lieb-Tasaki state on the honeycomb lattice is a universal resource for quantum computation". Physical Review A 86 (32328): 032328. doi:10.1103/PhysRevA.86.032328. Bibcode: 2012PhRvA..86c2328W. 
  45. ↑ Akimasa Miyake (2011). "Quantum computational capability of a 2D valence bond solid phase". Annals of Physics 236 (7): 1656–1671. doi:10.1016/j.aop.2011.03.006. Bibcode: 2011AnPhy.326.1656M. 
  46. ↑ Tzu-Chieh Wei; Poya Haghnegahdar; Robert Raussendorf (2014). "Spin mixture AKLT states for universal quantum computation". Physical Review A 90 (4): 042333. doi:10.1103/PhysRevA.90.042333. Bibcode: 2014PhRvA..90d2333W. 
General



Retrieved from "https://handwiki.org/wiki/index.php?title=One-way_quantum_computer&oldid=3379376"