Runcinated 5-cubes
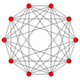
| 150px 5-cube |
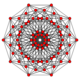
150px Runcinated 5-cube |
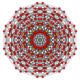
150px Runcinated 5-orthoplex |
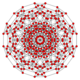
| 150px Runcitruncated 5-cube |
150px Runcicantellated 5-cube |
150px Runcicantitruncated 5-cube |
| 150px Runcitruncated 5-orthoplex |
150px Runcicantellated 5-orthoplex |
150px Runcicantitruncated 5-orthoplex |
| Orthogonal projections in B5 Coxeter plane | ||
|---|---|---|
In five-dimensional geometry, a runcinated 5-cube is a convex uniform 5-polytope that is a runcination (a 3rd order truncation) of the regular 5-cube.
There are 8 unique degrees of runcinations of the 5-cube, along with permutations of truncations and cantellations. Four are more simply constructed relative to the 5-orthoplex.
Runcinated 5-cube
| Runcinated 5-cube | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | t0,3{4,3,3,3} | |
| Coxeter diagram | ||
| 4-faces | 202 | 10 80 80 32 |
| Cells | 1240 | 40 240 320 160 320 160 |
| Faces | 2160 | 240 960 640 320 |
| Edges | 1440 | 480+960 |
| Vertices | 320 | |
| Vertex figure | 80px | |
| Coxeter group | B5 [4,3,3,3] | |
| Properties | convex | |
Alternate names
- Small prismated penteract (Acronym: span) (Jonathan Bowers)
Coordinates
The Cartesian coordinates of the vertices of a runcinated 5-cube having edge length 2 are all permutations of:
Images
| Coxeter plane | B5 | B4 / D5 | B3 / D4 / A2 |
|---|---|---|---|
| Graph | 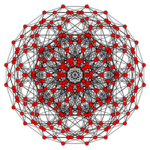
|
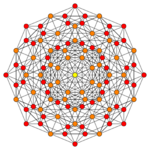
|
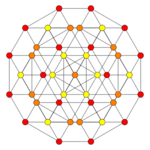
|
| Dihedral symmetry | [10] | [8] | [6] |
| Coxeter plane | B2 | A3 | |
| Graph | 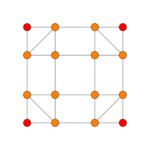
|
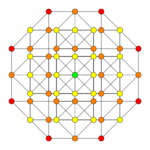
| |
| Dihedral symmetry | [4] | [4] |
Runcitruncated 5-cube
| Runcitruncated 5-cube | ||
|---|---|---|
| Type | Uniform 5-polytope | |
| Schläfli symbol | t0,1,3{4,3,3,3} | |
| Coxeter-Dynkin diagrams | ||
| 4-faces | 202 | 10 80 80 32 |
| Cells | 1560 | 40 240 320 320 160 320 160 |
| Faces | 3760 | 240 960 320 960 640 640 |
| Edges | 3360 | 480+960+1920 |
| Vertices | 960 | |
| Vertex figure | 80px | |
| Coxeter group | B5, [3,3,3,4] | |
| Properties | convex | |
Alternate names
- Runcitruncated penteract
- Prismatotruncated penteract (Acronym: pattin) (Jonathan Bowers)
Construction and coordinates
The Cartesian coordinates of the vertices of a runcitruncated 5-cube having edge length 2 are all permutations of:
Images
| Coxeter plane | B5 | B4 / D5 | B3 / D4 / A2 |
|---|---|---|---|
| Graph | 
|
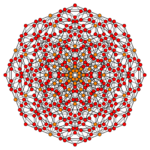
|
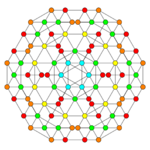
|
| Dihedral symmetry | [10] | [8] | [6] |
| Coxeter plane | B2 | A3 | |
| Graph | 
|
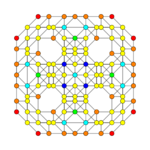
| |
| Dihedral symmetry | [4] | [4] |
Runcicantellated 5-cube
| Runcicantellated 5-cube | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | t0,2,3{4,3,3,3} | |
| Coxeter-Dynkin diagram | ||
| 4-faces | 202 | 10 80 80 32 |
| Cells | 1240 | 40 240 320 320 160 160 |
| Faces | 2960 | 240 480 960 320 640 320 |
| Edges | 2880 | 960+960+960 |
| Vertices | 960 | |
| Vertex figure | 80px | |
| Coxeter group | B5 [4,3,3,3] | |
| Properties | convex | |
Alternate names
- Runcicantellated penteract
- Prismatorhombated penteract (Acronym: prin) (Jonathan Bowers)
Coordinates
The Cartesian coordinates of the vertices of a runcicantellated 5-cube having edge length 2 are all permutations of:
Images
| Coxeter plane | B5 | B4 / D5 | B3 / D4 / A2 |
|---|---|---|---|
| Graph | 
|
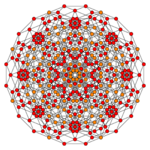
|
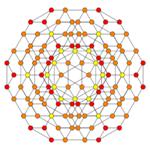
|
| Dihedral symmetry | [10] | [8] | [6] |
| Coxeter plane | B2 | A3 | |
| Graph | 
|
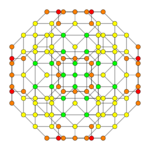
| |
| Dihedral symmetry | [4] | [4] |
Runcicantitruncated 5-cube
| Runcicantitruncated 5-cube | ||
| Type | Uniform 5-polytope | |
| Schläfli symbol | t0,1,2,3{4,3,3,3} | |
| Coxeter-Dynkin diagram |
||
| 4-faces | 202 | |
| Cells | 1560 | |
| Faces | 4240 | |
| Edges | 4800 | |
| Vertices | 1920 | |
| Vertex figure | 80px Irregular 5-cell | |
| Coxeter group | B5 [4,3,3,3] | |
| Properties | convex, isogonal | |
Alternate names
- Runcicantitruncated penteract
- Biruncicantitruncated pentacross
- great prismated penteract ( ) (Jonathan Bowers)
Coordinates
The Cartesian coordinates of the vertices of a runcicantitruncated 5-cube having an edge length of 2 are given by all permutations of coordinates and sign of:
Images
| Coxeter plane | B5 | B4 / D5 | B3 / D4 / A2 |
|---|---|---|---|
| Graph | Error creating thumbnail: Unable to save thumbnail to destination | 
|
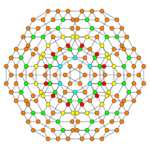
|
| Dihedral symmetry | [10] | [8] | [6] |
| Coxeter plane | B2 | A3 | |
| Graph | 
|
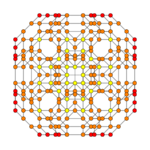
| |
| Dihedral symmetry | [4] | [4] |
Related polytopes
These polytopes are a part of a set of 31 uniform polytera generated from the regular 5-cube or 5-orthoplex.
References
- H.S.M. Coxeter:
- H.S.M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [1]
- (Paper 22) H.S.M. Coxeter, Regular and Semi Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Norman Johnson Uniform Polytopes, Manuscript (1991)
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D.
- Klitzing, Richard. "5D uniform polytopes (polytera)". https://bendwavy.org/klitzing/dimensions/polytera.htm. o3x3o3o4x - span, o3x3o3x4x - pattin, o3x3x3o4x - prin, o3x3x3x4x - gippin
External links
- Glossary for hyperspace, George Olshevsky.
- Polytopes of Various Dimensions, Jonathan Bowers
- Runcinated uniform polytera (spid), Jonathan Bowers
- Multi-dimensional Glossary
Fundamental convex regular and uniform polytopes in dimensions 2–10
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 |