2 31 polytope
 321 |
 231 |
 132 | |||
 Rectified 321 |
 birectified 321 | ||||
 Rectified 231 |
 Rectified 132 | ||||
| Orthogonal projections in E7 Coxeter plane | |||||
|---|---|---|---|---|---|
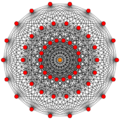
In 7-dimensional geometry, 231 is a uniform polytope, constructed from the E7 group.
Its Coxeter symbol is 231, describing its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 2-node branch.
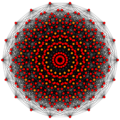
The rectified 231 is constructed by points at the mid-edges of the 231.
These polytopes are part of a family of 127 (or 27−1) convex uniform polytopes in 7-dimensions, made of uniform polytope facets and vertex figures, defined by all permutations of rings in this Coxeter-Dynkin diagram: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
2_31 polytope
| Gosset 231 polytope | |
|---|---|
| Type | Uniform 7-polytope |
| Family | 2k1 polytope |
| Schläfli symbol | {3,3,33,1} |
| Coxeter symbol | 231 |
| Coxeter diagram | |
| 6-faces | 632: 56 221 576 {35} |
| 5-faces | 4788: 756 211 4032 {34} |
| 4-faces | 16128: 4032 201 12096 {33} |
| Cells | 20160 {32} |
| Faces | 10080 {3} |
| Edges | 2016 |
| Vertices | 126 |
| Vertex figure | 131 |
| Petrie polygon | Octadecagon |
| Coxeter group | E7, [33,2,1] |
| Properties | convex |
The 231 is composed of 126 vertices, 2016 edges, 10080 faces (Triangles), 20160 cells (tetrahedra), 16128 4-faces (3-simplexes), 4788 5-faces (756 pentacrosses, and 4032 5-simplexes), 632 6-faces (576 6-simplexes and 56 221). Its vertex figure is a 6-demicube. Its 126 vertices represent the root vectors of the simple Lie group E7.
This polytope is the vertex figure for a uniform tessellation of 7-dimensional space, 331.
Alternate names
- E. L. Elte named it V126 (for its 126 vertices) in his 1912 listing of semiregular polytopes.[1]
- It was called 231 by Coxeter for its bifurcating Coxeter-Dynkin diagram, with a single ring on the end of the 2-node sequence.
- Pentacontihexa-pentacosiheptacontihexa-exon (Acronym laq) - 56-576 facetted polyexon (Jonathan Bowers)[2]
Construction
It is created by a Wythoff construction upon a set of 7 hyperplane mirrors in 7-dimensional space.
The facet information can be extracted from its Coxeter-Dynkin diagram, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Removing the node on the short branch leaves the 6-simplex. There are 576 of these facets. These facets are centered on the locations of the vertices of the 321 polytope, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Removing the node on the end of the 3-length branch leaves the 221. There are 56 of these facets. These facets are centered on the locations of the vertices of the 132 polytope, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
The vertex figure is determined by removing the ringed node and ringing the neighboring node. This makes the 6-demicube, 131, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Seen in a configuration matrix, the element counts can be derived by mirror removal and ratios of Coxeter group orders.[3]
| E7 | k-face | fk | f0 | f1 | f2 | f3 | f4 | f5 | f6 | k-figures | notes | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| D6 | ( ) | f0 | 126 | 32 | 240 | 640 | 160 | 480 | 60 | 192 | 12 | 32 | 6-demicube | E7/D6 = 72x8!/32/6! = 126 | |
| A5A1 | { } | f1 | 2 | 2016 | 15 | 60 | 20 | 60 | 15 | 30 | 6 | 6 | rectified 5-simplex | E7/A5A1 = 72x8!/6!/2 = 2016 | |
| A3A2A1 | {3} | f2 | 3 | 3 | 10080 | 8 | 4 | 12 | 6 | 8 | 4 | 2 | tetrahedral prism | E7/A3A2A1 = 72x8!/4!/3!/2 = 10080 | |
| A3A2 | {3,3} | f3 | 4 | 6 | 4 | 20160 | 1 | 3 | 3 | 3 | 3 | 1 | tetrahedron | E7/A3A2 = 72x8!/4!/3! = 20160 | |
| A4A2 | {3,3,3} | f4 | 5 | 10 | 10 | 5 | 4032 | * | 3 | 0 | 3 | 0 | {3} | E7/A4A2 = 72x8!/5!/3! = 4032 | |
| A4A1 | 5 | 10 | 10 | 5 | * | 12096 | 1 | 2 | 2 | 1 | Isosceles triangle | E7/A4A1 = 72x8!/5!/2 = 12096 | |||
| D5A1 | {3,3,3,4} | f5 | 10 | 40 | 80 | 80 | 16 | 16 | 756 | * | 2 | 0 | { } | E7/D5A1 = 72x8!/32/5! = 756 | |
| A5 | {3,3,3,3} | 6 | 15 | 20 | 15 | 0 | 6 | * | 4032 | 1 | 1 | E7/A5 = 72x8!/6! = 72*8*7 = 4032 | |||
| E6 | {3,3,32,1} | f6 | 27 | 216 | 720 | 1080 | 216 | 432 | 27 | 72 | 56 | * | ( ) | E7/E6 = 72x8!/72x6! = 8*7 = 56 | |
| A6 | {3,3,3,3,3} | 7 | 21 | 35 | 35 | 0 | 21 | 0 | 7 | * | 576 | E7/A6 = 72x8!/7! = 72×8 = 576 | |||
Images
| E7 | E6 / F4 | B6 / A6 |
|---|---|---|
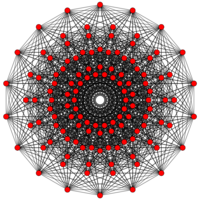 [18] |
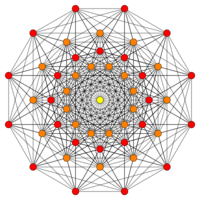 [12] |
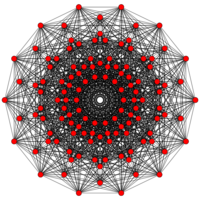 [7x2] |
| A5 | D7 / B6 | D6 / B5 |
 [6] |
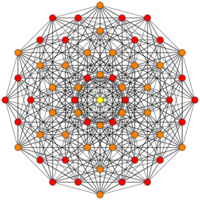 [12/2] |
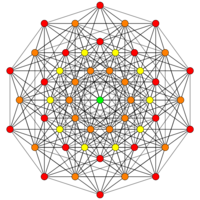 [10] |
| D5 / B4 / A4 | D4 / B3 / A2 / G2 | D3 / B2 / A3 |
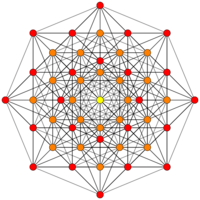 [8] |
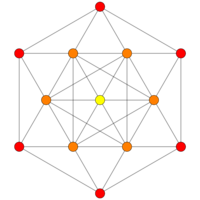 [6] |
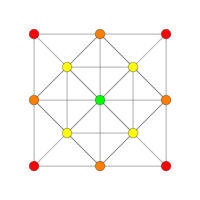 [4] |
Related polytopes and honeycombs
Rectified 2_31 polytope
| Rectified 231 polytope | |
|---|---|
| Type | Uniform 7-polytope |
| Family | 2k1 polytope |
| Schläfli symbol | {3,3,33,1} |
| Coxeter symbol | t1(231) |
| Coxeter diagram | |
| 6-faces | 758 |
| 5-faces | 10332 |
| 4-faces | 47880 |
| Cells | 100800 |
| Faces | 90720 |
| Edges | 30240 |
| Vertices | 2016 |
| Vertex figure | 6-demicube |
| Petrie polygon | Octadecagon |
| Coxeter group | E7, [33,2,1] |
| Properties | convex |
The rectified 231 is a rectification of the 231 polytope, creating new vertices on the center of edge of the 231.
Alternate names
- Rectified pentacontihexa-pentacosiheptacontihexa-exon - as a rectified 56-576 facetted polyexon (acronym rolaq) (Jonathan Bowers)[4]
Construction
It is created by a Wythoff construction upon a set of 7 hyperplane mirrors in 7-dimensional space.
The facet information can be extracted from its Coxeter-Dynkin diagram, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Removing the node on the short branch leaves the rectified 6-simplex, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Removing the node on the end of the 2-length branch leaves the, 6-demicube,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Removing the node on the end of the 3-length branch leaves the rectified 221, ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
The vertex figure is determined by removing the ringed node and ringing the neighboring node.
Images
| E7 | E6 / F4 | B6 / A6 |
|---|---|---|
 [18] |
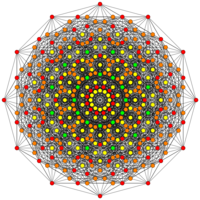 [12] |
 [7x2] |
| A5 | D7 / B6 | D6 / B5 |
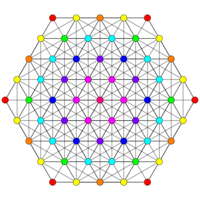 [6] |
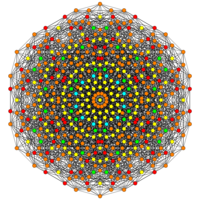 [12/2] |
 [10] |
| D5 / B4 / A4 | D4 / B3 / A2 / G2 | D3 / B2 / A3 |
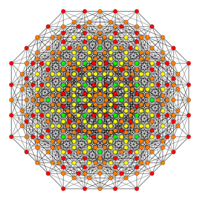 [8] |
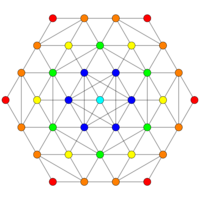 [6] |
 [4] |
See also
- List of E7 polytopes
Notes
References
- Elte, E. L. (1912), The Semiregular Polytopes of the Hyperspaces, Groningen: University of Groningen
- H. S. M. Coxeter, Regular Polytopes, 3rd Edition, Dover New York, 1973
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN:978-0-471-01003-6 [1]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- Klitzing, Richard. "7D uniform polytopes (polyexa)". https://bendwavy.org/klitzing/dimensions/polyexa.htm. x3o3o3o *c3o3o3o - laq, o3x3o3o *c3o3o3o - rolaq
Fundamental convex regular and uniform polytopes in dimensions 2–10
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 |

