Interior-point method

Short description: Algorithms for solving convex optimization problems

Example search for a solution. Blue lines show constraints, red points show iterated solutions.

Interior-point methods (also referred to as barrier methods or IPMs) are algorithms for solving linear and non-linear convex optimization problems. IPMs combine two advantages of previously-known algorithms:

• Theoretically, their run-time is polynomial—in contrast to the simplex method, which has exponential run-time in the worst case.
• Practically, they run as fast as the simplex method—in contrast to the ellipsoid method, which has polynomial run-time in theory but is very slow in practice.

In contrast to the simplex method which traverses the boundary of the feasible region, and the ellipsoid method which bounds the feasible region from outside, an IPM reaches a best solution by traversing the interior of the feasible region—hence the name.

History

An interior point method was discovered by Soviet mathematician I. I. Dikin in 1967. The method was reinvented in the U.S. in the mid-1980s. In 1984, Narendra Karmarkar developed a method for linear programming called Karmarkar's algorithm, which runs in provably polynomial time ([math]\displaystyle{ O(n^{3.5} L) }[/math] operations on L-bit numbers, where n is the number of variables and constants), and is also very efficient in practice. Karmarkar's paper created a surge of interest in interior point methods. Two years later, James Renegar invented the first path-following interior-point method, with run-time [math]\displaystyle{ O(n^{3} L) }[/math]. The method was later extended from linear to convex optimization problems, based on a self-concordant barrier function used to encode the convex set.

Any convex optimization problem can be transformed into minimizing (or maximizing) a linear function over a convex set by converting to the epigraph form. The idea of encoding the feasible set using a barrier and designing barrier methods was studied by Anthony V. Fiacco, Garth P. McCormick, and others in the early 1960s. These ideas were mainly developed for general nonlinear programming, but they were later abandoned due to the presence of more competitive methods for this class of problems (e.g. sequential quadratic programming).

Yurii Nesterov and Arkadi Nemirovski came up with a special class of such barriers that can be used to encode any convex set. They guarantee that the number of iterations of the algorithm is bounded by a polynomial in the dimension and accuracy of the solution.

The class of primal-dual path-following interior-point methods is considered the most successful. Mehrotra's predictor–corrector algorithm provides the basis for most implementations of this class of methods.

Definitions

We are given a convex program of the form:[math]\displaystyle{ \begin{aligned} \underset{x \in \mathbb{R}^n}{\text{minimize}}\quad & f(x) \\ \text{subject to}\quad & x \in G. \end{aligned} }[/math]where f is a convex function and G is a convex set. Without loss of generality, we can assume that the objective f is a linear function. Usually, the convex set G is represented by a set of convex inequalities and linear equalities; the linear equalities can be eliminated using linear algebra, so for simplicity we assume there are only convex inequalities, and the program can be described as follows, where the g_i are convex functions:[math]\displaystyle{ \begin{aligned} \underset{x \in \mathbb{R}^n}{\text{minimize}}\quad & f(x) \\ \text{subject to}\quad & g_i(x) \leq 0 \text{ for } i = 1, \dots, m. \\ \end{aligned} }[/math]We assume that the constraint functions belong to some family (e.g. quadratic functions), so that the program can be represented by a finite vector of coefficients (e.g. the coefficients to the quadratic functions). The dimension of this coefficient vector is called the size of the program. A numerical solver for a given family of programs is an algorithm that, given the coefficient vector, generates a sequence of approximate solutions x_t for t=1,2,..., using finitely many arithmetic operations. A numerical solver is called convergent if, for any progarm from the family and any positive ε>0, there is some T (which may depend on the program and on ε) such that, for any t>T, the approximate solution x_t is ε-approximate, that is:

f(x) - f^* ≤ ε

g_i(x) ≤ ε for i in 1,...,m,

x in G,

where f^* is the optimal solution. A solver is called polynomial if the total number of arithmetic operations in the first T steps is at most

poly(problem-size) * log(V/ε),

where V is some data-dependent constant, e.g., the difference between the largest and smallest value in the feasible set. In other words, V/ε is the "relative accuracy" of the solution - the accuracy w.r.t. the largest coefficient. log(V/ε) represents the number of "accuracy digits". Therefore, a solver is 'polynomial' if each additional digit of accuracy requires a number of operations that is polynomial in the problem size.

Types

Types of interior point methods include:

• Potential reduction methods: Karmarkar's algorithm was the first one.
• Path-following methods: the algorithms of James Renegar and Clovis Gonzaga were the first ones.
• Primal-dual methods.

Path-following methods

Idea

Given a convex optimization program (P) with constraints, we can convert it to an unconstrained program by adding a barrier function. Specifically, let b be a smooth convex function, defined in the interior of the feasible region G, such that for any sequence {x_j in interior(G)} whose limit is on the boundary of G: [math]\displaystyle{ \lim_{j\to \infty} b(x_j)=\infty }[/math]. We also assume that b is non-degenerate, that is: [math]\displaystyle{ b''(x) }[/math] is positive definite for all x in interior(G). Now, consider the family of programs:

(P_t) minimize t * f(x) + b(x)

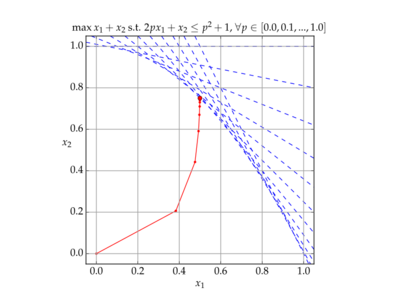
Technically the program is restricted, since b is defined only in the interior of G. But practically, it is possible to solve it as an unconstrained program, since any solver trying to minimize the function will not approach the boundary, where b approaches infinity. Therefore, (P_t) has a unique solution - denote it by x*(t). The function x* is a continuous function of t, which is called the central path. All limit points of x*, as t approaches infinity, are optimal solutions of the original program (P).

A path-following method is a method of tracking the function x* along a certain increasing sequence t₁,t₂,..., that is: computing a good-enough approximation x_i to the point x*(t_i), such that the difference x_i - x*(t_i) approaches 0 as i approaches infinity; then the sequence x_i approaches the optimal solution of (P). This requires to specify three things:

• The barrier function b(x).
• A policy for determining the penalty parameters t_i.
• The unconstrained-optimization solver used to solve (P_i) and find x_i, such as Newton's method. Note that we can use each x_i as a starting-point for solving the next problem (P_i+1).

The main challenge in proving that the method is polytime is that, as the penalty parameter grows, the solution gets near the boundary, and the function becomes steeper. The run-time of solvers such as Newton's method becomes longer, and it is hard to prove that the total runtime is polynomial.

Renegar and Gonzaga proved that a specific instance of a path-following method is polytime:

• The constraints (and the objective) are linear functions;
• The barrier function is logarithmic: b(x) := - sum_j log(-g_j(x)).
• The penalty parameter t is updated geometrically, that is, [math]\displaystyle{ t_{i+1} := \mu \cdot t_i }[/math], where μ is a constant (they took [math]\displaystyle{ \mu = 1+0.001\cdot \sqrt{m} }[/math],where m is the number of inequality constraints);
• The solver is Newton's method, and a single step of Newton is done for each single step in t.

They proved that, in this case, the difference x_i - x*(t_i) remains at most 0.01, and f(x_i) - f* is at most 2*m/t_i. Thus, the solution accuracy is proportional to 1/t_i, so to add a single accuracy-digit, it is suffiicent to multiply t_i by 2 (or any other constant factor), which requires O(sqrt(m)) Newton steps. Since each Newton step takes O(m n²) operations, the total complexity is O(m^3/2 n²) operations for accuracy digit.

Yuri Nesterov extended the idea from linear to non-linear programs. He noted that the main property of the logarithmic barrier, used in the above proofs, is that it is self-concordant with a finite barrier parameter. Therefore, many other classes of convex programs can be solved in polytime using a path-following method, if we can find a suitable self-concordant barrier function for their feasible region.

Details

We are given a convex optimization problem (P) in "standard form":

minimize c^Tx s.t. x in G,

where G is convex and closed. We can also assume that G is bounded (we can easily make it bounded by adding a constraint |x|≤R for some sufficiently large R).

To use the interior-point method, we need a self-concordant barrier for G. Let b be an M-self-concordant barrier for G, where M≥1 is the self-concordance parameter. We assume that we can compute efficiently the value of b, its gradient, and its Hessian, for every point x in the interior of G.

For every t>0, we define the penalized objective f_t(x) := c^Tx + b(x). We define the path of minimizers by: x*(t) := arg min f_t(x). We apporimate this path along an increasing sequence t_i. The sequence is initialized by a certain non-trivial two-phase initialization procedure. Then, it is updated according to the following rule: [math]\displaystyle{ t_{i+1} := \mu \cdot t_i }[/math].

For each t_i, we find an approximate minimum of f_ti, denoted by x_i. The approximate minimum is chosen to satisfy the following "closeness condition" (where L is the path tolerance):

[math]\displaystyle{ \sqrt{[\nabla_x f_t(x_i)]^T [\nabla_x^2 f_t(x_i)]^{-1} [\nabla_x f_t(x_i)]} \leq L }[/math].

To find x_i+1, we start with x_i and apply the damped Newton method. We apply several steps of this method, until the above "closeness relation" is satisfied. The first point that satisfies this relation is denoted by x_i+1.

Convergence and complexity

The convergence rate of the method is given by the following formula, for every i:

[math]\displaystyle{ c^T x_i - c^* \leq \frac{2 M}{t_0} \mu^{-i} }[/math]

Taking [math]\displaystyle{ \mu = \left(1+r/\sqrt{M}\right) }[/math], the number of Newton steps required to go from x_i to x_i+1 is at most a fixed number, that depends only on r and L. In particular, the total number of Newton steps required to find an ε-approximate solution (i.e., finding x in G such that c^Tx - c* ≤ ε) is at most:

[math]\displaystyle{ O(1) \cdot \sqrt{M} \cdot \ln\left(\frac{M}{t_0 \varepsilon} + 1\right) }[/math]

where the constant factor O(1) depends only on r and L. The number of Newton steps required for the two-step initialization procedure is at most:

[math]\displaystyle{ O(1) \cdot \sqrt{M} \cdot \ln\left(\frac{M}{1-\pi_{x^*_f}(\bar{x})} + 1\right) + O(1) \cdot \sqrt{M} \cdot \ln\left(\frac{M \text{Var}_G(c)}{\epsilon} + 1\right) }[/math]

where the constant factor O(1) depends only on r and L, and [math]\displaystyle{ \text{Var}_G(c) := \max_{x\in G} c^T x - \min_{x\in G} c^T x }[/math], and [math]\displaystyle{ \bar{x} }[/math] is some point in the interior of G. Overall, the overall Newton complexity of finding an ε-approximate solution is at most

[math]\displaystyle{ O(1) \cdot \sqrt{M} \cdot \ln\left(\frac{V}{\varepsilon} + 1\right) }[/math], where V is some problem-dependent constant: [math]\displaystyle{ V = \frac{\text{Var}_G(c)}{1-\pi_{x^*_f(\bar{x})}} }[/math].

Each Newton step takes O(n³) arithmetic operations.

Initialization: phase-I methods

To initialize the path-following methods, we need a point in the relative interior of the feasible region G. In other words: if G is defined by the inequalities g_i(x) ≤ 0, then we need some x for which g_i(x) < 0 for all i in 1,...,m. If we do not have such a point, we need to find one using a so-called phase I method. A simple phase-I method is to solve the following convex program:[math]\displaystyle{ \begin{aligned} \text{minimize}\quad & s \\ \text{subject to}\quad & g_i(x) \leq s \text{ for } i = 1, \dots, m \end{aligned} }[/math]Denote the optimal solution by x*,s*.

• If s*<0, then we know that x* is an interior point of the original problem and can go on to "phase II", which is solving the original problem.
• If s*>0, then we know that the original program is infeasible - the feasible region is empty.
• If s*=0 and it is attained by some solution x*, then the problem is feasible but has no interior point; if it is not attained, then the problem is infeasible.

For this program it is easy to get an interior point: we can take arbitrarily x=0, and take s to be any number larger than max(f₁(0),...,f_m(0)). Therefore, it can be solved using interior-point methods. However, the run-time is proportional to log(1/s*). As s* comes near 0, it becomes harder and harder to find an exact solution to the phase-I problem, and thus harder to decide whether the original problem is feasible.

Practical considerations

The theoretic guarantees assume that the penalty parameter is increased at the rate [math]\displaystyle{ \mu = \left(1+r/\sqrt{M}\right) }[/math], so the worst-case number of required Newton steps is [math]\displaystyle{ O(\sqrt{M}) }[/math]. In theory, if μ is larger (e.g. 2 or more), then the worst-case number of required Newton steps is in [math]\displaystyle{ O(M) }[/math]. However, in practice, larger μ leads to a much faster convergence. These methods are called long-step methods. In practice, if μ is between 3 and 100, then the program converges within 20-40 Newton steps, regardless of the number of constraints (though the runtime of each Newton step of course grows with the number of constraints). The exact value of μ within this range has little effect on the performane.

Potential-reduction methods

For potential-reduction methods, the problem is presented in the conic form:

minimize c^Tx s.t. x in {b+L} ᚢ K,

where b is a vector in Rⁿ, L is a linear subspace in Rⁿ (so b+L is an affine plane), and K is a closed pointed convex cone with a nonempty interior. Every convex program can be converted to the conic form. To use the potential-reduction method (specifically, the extension of Karmarkar's algorithm to convex programming), we need the following assumptions:

• A. The feasible set {b+L} ᚢ K is bounded, and intersects the interior of the cone K.
• B. We are given in advance a strictly-feasible solution x^, that is, a feasible solution in the interior of K.
• C. We know in advance the optimal objective value, c*, of the problem.
• D. We are given an M-logarithmically-homogeneous self-concordant barrier F for the cone K.

Assumptions A, B and D are needed in most interior-point methods. Assumption C is specific to Karmarkar's approach; it can be alleviated by using a "sliding objective value". It is possible to further reduce the program to the Karmarkar format:

minimize s^Tx s.t. x in M ᚢ K and e^Tx = 1

where M is a linear subspace of in Rⁿ, and the optimal objective value is 0. The method is based on the following scalar potential function:

v(x) = F(x) + M ln (s^Tx)

where F is the M-self-concordant barrier for the feasible cone. It is possible to prove that, when x is strictly feasible and v(x) is very small (- very negative), x is approximately-optimal. The idea of the potential-reduction method is to modify x such that the potential at each iteration drops by at least a fixed constant X (specifically, X=1/3-ln(4/3)). This implies that, after i iterations, the difference between objective value and the optimal objective value is at most V * exp(-i X / M), where V is a data-dependent constant. Therefore, the number of Newton steps required for an ε-approximate solution is at most [math]\displaystyle{ O(1) \cdot M \cdot \ln\left(\frac{V}{\varepsilon} + 1\right)+1 }[/math].

Note that in path-following methods the expression is [math]\displaystyle{ \sqrt{M} }[/math] rather than M, which is better in theory. But in practice, Karmarkar's method allows taking much larger steps towards the goal, so it may converge much faster than the theoretical guarantees.

Primal-dual methods

The primal-dual method's idea is easy to demonstrate for constrained nonlinear optimization. For simplicity, consider the following nonlinear optimization problem with inequality constraints:

[math]\displaystyle{ \begin{aligned} \operatorname{minimize}\quad & f(x) \\ \text{subject to}\quad &x \in \mathbb{R}^n,\\ &c_i(x) \ge 0 \text{ for } i = 1, \ldots, m,\\ \text{where}\quad & f : \mathbb{R}^{n} \to \mathbb{R},\ c_i : \mathbb{R}^{n} \to \mathbb{R}. \end{aligned}\quad (1) }[/math]

This inequality-constrained optimization problem is solved by converting it into an unconstrained objective function whose minimum we hope to find efficiently. Specifically, the logarithmic barrier function associated with (1) is [math]\displaystyle{ B(x,\mu) = f(x) - \mu \sum_{i=1}^m \log(c_i(x)). \quad (2) }[/math]

Here [math]\displaystyle{ \mu }[/math] is a small positive scalar, sometimes called the "barrier parameter". As [math]\displaystyle{ \mu }[/math] converges to zero the minimum of [math]\displaystyle{ B(x,\mu) }[/math] should converge to a solution of (1).

The gradient of a differentiable function [math]\displaystyle{ h : \mathbb{R}^n \to \mathbb{R} }[/math] is denoted [math]\displaystyle{ \nabla h }[/math]. The gradient of the barrier function is [math]\displaystyle{ \nabla B(x,\mu) = \nabla f(x) - \mu \sum_{i=1}^m \frac{1}{c_i(x)} \nabla c_i(x). \quad (3) }[/math]

In addition to the original ("primal") variable [math]\displaystyle{ x }[/math] we introduce a Lagrange multiplier-inspired dual variable [math]\displaystyle{ \lambda \in \mathbb{R} ^m }[/math] [math]\displaystyle{ c_i(x) \lambda_i = \mu,\quad \forall i = 1, \ldots, m. \quad (4) }[/math]

Equation (4) is sometimes called the "perturbed complementarity" condition, for its resemblance to "complementary slackness" in KKT conditions.

We try to find those [math]\displaystyle{ (x_\mu, \lambda_\mu) }[/math] for which the gradient of the barrier function is zero.

Substituting [math]\displaystyle{ 1/c_i(x) = \lambda_i / \mu }[/math] from (4) into (3), we get an equation for the gradient: [math]\displaystyle{ \nabla B(x_\mu, \lambda_\mu) = \nabla f(x_\mu) - J(x_\mu)^T \lambda_\mu = 0, \quad (5) }[/math] where the matrix [math]\displaystyle{ J }[/math] is the Jacobian of the constraints [math]\displaystyle{ c(x) }[/math].

The intuition behind (5) is that the gradient of [math]\displaystyle{ f(x) }[/math] should lie in the subspace spanned by the constraints' gradients. The "perturbed complementarity" with small [math]\displaystyle{ \mu }[/math] (4) can be understood as the condition that the solution should either lie near the boundary [math]\displaystyle{ c_i(x) = 0 }[/math], or that the projection of the gradient [math]\displaystyle{ \nabla f }[/math] on the constraint component [math]\displaystyle{ c_i(x) }[/math] normal should be almost zero.

Let [math]\displaystyle{ (p_x, p_\lambda) }[/math] be the search direction for iteratively updating [math]\displaystyle{ (x, \lambda) }[/math]. Applying Newton's method to (4) and (5), we get an equation for [math]\displaystyle{ (p_x, p_\lambda) }[/math]: [math]\displaystyle{ \begin{pmatrix} H(x, \lambda) & -J(x)^T \\ \operatorname{diag}(\lambda) J(x) & \operatorname{diag}(c(x)) \end{pmatrix}\begin{pmatrix} p_x \\ p_\lambda \end{pmatrix}=\begin{pmatrix} -\nabla f(x) + J(x)^T \lambda \\ \mu 1 - \operatorname{diag}(c(x)) \lambda \end{pmatrix}, }[/math]

where [math]\displaystyle{ H }[/math] is the Hessian matrix of [math]\displaystyle{ B(x, \mu) }[/math], [math]\displaystyle{ \operatorname{diag}(\lambda) }[/math] is a diagonal matrix of [math]\displaystyle{ \lambda }[/math], and [math]\displaystyle{ \operatorname{diag}(c(x)) }[/math] is the diagonal matrix of [math]\displaystyle{ c(x) }[/math].

Because of (1), (4) the condition

[math]\displaystyle{ \lambda \ge 0 }[/math]

should be enforced at each step. This can be done by choosing appropriate [math]\displaystyle{ \alpha }[/math]:

[math]\displaystyle{ (x,\lambda) \to (x + \alpha p_x, \lambda + \alpha p_\lambda). }[/math]File:Interior Point Trajectory.webm

Types of Convex Programs Solvable via Interior-Point Methods

Here are some special cases of convex programs that can be solved efficiently by interior-point methods.

Linear programs

Consider a linear program of the form: [math]\displaystyle{ \begin{aligned} \operatorname{minimize}\quad & c^\top x \\ \text{subject to}\quad & Ax \leq b. \end{aligned}. }[/math] We can apply path-following methods with the barrier [math]\displaystyle{ b(x) := -\sum_{j=1}^m \ln(b_j - a_j^T x). }[/math] The function [math]\displaystyle{ b }[/math] is self-concordant with parameter M=m (the number of constraints). Therefore, the number of required Newton steps for the path-following method is O(mn²), and the total runtime complexity is O(m^3/2 n²).

Quadratically constrained quadratic programs

Given a quadratically constrained quadratic program of the form: [math]\displaystyle{ \begin{aligned} \operatorname{minimize}\quad & d^\top x \\ \text{subject to}\quad & f_j(x) := x^\top A_j x + b_j^\top x + c_j \leq 0 \quad \text{ for all } j = 1, \dots, m, \end{aligned} }[/math] where all matrices A_j are positive-semidefinite matrices. We can apply path-following methods with the barrier [math]\displaystyle{ b(x) := -\sum_{j=1}^m \ln(-f_j(x)). }[/math] The function [math]\displaystyle{ b }[/math] is a self-concordant barrier with parameter M=m. The Newton complexity is O((m+n)n²), and the total runtime complexity is O(m^1/2 (m+n) n²).

L_p norm approximation

Consider a problem of the form [math]\displaystyle{ \begin{aligned} \operatorname{minimize}\quad & \sum_j |v_j - u_j^\top x|_p \end{aligned}, }[/math] where each [math]\displaystyle{ u_j }[/math] is a vector, each [math]\displaystyle{ v_j }[/math] is a scalar, and [math]\displaystyle{ |\cdot|_p }[/math] is an L_p norm with [math]\displaystyle{ 1\lt p \lt \infty. }[/math] After converting to the standard form, we can apply path-following methods with a self-concordant barrier with parameter M=4m. The Newton complexity is O((m+n)n²), and the total runtime complexity is O(m^1/2 (m+n) n²).

Geometric programs

Consider the problem

[math]\displaystyle{ \begin{aligned} \operatorname{minimize}\quad & f_0(x) := \sum_{i=1}^k c_{i0} \exp(a_i^\top x) \\ \text{subject to}\quad & f_j(x) := \sum_{i=1}^k c_{ij} \exp(a_i^\top x) \leq d_j \quad \text{ for all } j = 1, \dots, m. \end{aligned} }[/math]

There is a self-concordant barrier with parameter 2k+m. The path-following method has Newton complexity O(mk²+k³+n³) and total complexity O((k+m)^1/2[mk²+k³+n³]).

Semidefinite programs

Interior point methods can be used to solve semidefinite programs.

See also

• Affine scaling
• Augmented Lagrangian method
• Chambolle-Pock algorithm
• Karush–Kuhn–Tucker conditions
• Penalty method

References

• Bonnans, J. Frédéric; Gilbert, J. Charles; Lemaréchal, Claude; Sagastizábal, Claudia A. (2006). Numerical optimization: Theoretical and practical aspects. Universitext (Second revised ed. of translation of 1997 French ed.). Berlin: Springer-Verlag. pp. xiv+490. doi:10.1007/978-3-540-35447-5. ISBN 978-3-540-35445-1. https://www.springer.com/mathematics/applications/book/978-3-540-35445-1. 
• Nocedal, Jorge; Stephen Wright (1999). Numerical Optimization. New York, NY: Springer. ISBN 978-0-387-98793-4. 
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007). "Section 10.11. Linear Programming: Interior-Point Methods". Numerical Recipes: The Art of Scientific Computing (3rd ed.). New York: Cambridge University Press. ISBN 978-0-521-88068-8. http://apps.nrbook.com/empanel/index.html#pg=537.