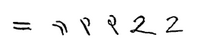2
| ||||
|---|---|---|---|---|
| Cardinal | two | |||
| Ordinal | 2nd (second / twoth) | |||
| Numeral system | binary | |||
| Factorization | prime | |||
| Gaussian integer factorization | [math]\displaystyle{ (1 + i)(1 - i) }[/math] | |||
| Prime | 1st | |||
| Divisors | 1, 2 | |||
| Greek numeral | Β´ | |||
| Roman numeral | II, ii | |||
| Greek prefix | di- | |||
| Latin prefix | duo-/bi- | |||
| Old English prefix | twi- | |||
| Binary | 102 | |||
| Ternary | 23 | |||
| Quaternary | 24 | |||
| Quinary | 25 | |||
| Senary | 26 | |||
| Octal | 28 | |||
| Duodecimal | 212 | |||
| Hexadecimal | 216 | |||
| Vigesimal | 220 | |||
| Base 36 | 236 | |||
| Greek numeral | β' | |||
| Arabic, Kurdish, Persian, Sindhi, Urdu | ٢ | |||
| Ge'ez | ፪ | |||
| Bengali | ২ | |||
| Chinese numeral | 二,弍,貳 | |||
| Devanāgarī | २ | |||
| Telugu | ౨ | |||
| Tamil | ௨ | |||
| Kannada | ೨ | |||
| Hebrew | ב | |||
| Khmer | ២ | |||
| Thai | ๒ | |||
| Georgian | Ⴁ/ⴁ/ბ(Bani) | |||
| Malayalam | ൨ | |||
2 (two) is a number, numeral and digit. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultures.
Evolution
Arabic digit
The digit used in the modern Western world to represent the number 2 traces its roots back to the Indic Brahmic script, where "2" was written as two horizontal lines. The modern Chinese and Japanese languages (and Korean Hanja) still use this method. The Gupta script rotated the two lines 45 degrees, making them diagonal. The top line was sometimes also shortened and had its bottom end curve towards the center of the bottom line. In the Nagari script, the top line was written more like a curve connecting to the bottom line. In the Arabic Ghubar writing, the bottom line was completely vertical, and the digit looked like a dotless closing question mark. Restoring the bottom line to its original horizontal position, but keeping the top line as a curve that connects to the bottom line leads to our modern digit.[1]
In fonts with text figures, digit 2 usually is of x-height, for example, ![]() .[citation needed]
.[citation needed]
As a word
Two is most commonly a determiner used with plural countable nouns, as in two days or I'll take these two.[2] Two is a noun when it refers to the number two as in two plus two is four.
Etymology of two
The word two is derived from the Old English words twā (feminine), tū (neuter), and twēġen (masculine, which survives today in the form twain).[3]
The pronunciation /tuː/, like that of who is due to the labialization of the vowel by the w, which then disappeared before the related sound. The successive stages of pronunciation for the Old English twā would thus be /twɑː/, /twɔː/, /twoː/, /twuː/, and finally /tuː/.[3]
Mathematics
Characterizations
The number two is the smallest, and only even, prime number. As the smallest prime number, two is also the smallest non-zero pronic number, and the only pronic prime.[4] An integer is determined to be even if it is divisible by 2. For integers written in a numeral system based on an even number such as decimal, divisibility by 2 is easily tested by merely looking at the last digit. If it is even, then the whole number is even. When written in the decimal system, all multiples of 2 will end in 0, 2, 4, 6, or 8.[5]
Every integer greater than 1 will have at least two distinct factors; by definition, a prime number only has two distinct factors (itself and 1). Therefore, the number-of-divisors function [math]\displaystyle{ d(n) }[/math] of positive integers [math]\displaystyle{ n }[/math] satisfies, [math]\displaystyle{ \liminf_{n\to\infty} d(n)=2, }[/math] where [math]\displaystyle{ \liminf }[/math] represents the limit inferior (since there will always exist a larger prime number with a maximum of two divisors).[6]
Specifically,
In a set-theoretical construction of the natural numbers, [math]\displaystyle{ 2 }[/math] is identified with the set [math]\displaystyle{ \{\{\varnothing\},\varnothing\} }[/math], where [math]\displaystyle{ \varnothing }[/math] denotes the empty set. This latter set is important in category theory: it is a subobject classifier in the category of sets. A Cantor space is a topological space [math]\displaystyle{ 2^\mathbb{N} }[/math] homeomorphic to the Cantor set, whose general set is a closed set consisting purely of boundary points. The countably infinite product topology of the simplest discrete two-point space, [math]\displaystyle{ \{0, 1\} }[/math], is the traditional elementary example of a Cantor space. More broadly, a set that is a field has a minimum of two elements.
The binary system has a radix of two, and it is the numeral system with the fewest tokens that allows denoting a natural number substantially more concisely (with [math]\displaystyle{ \log_{2} }[/math] [math]\displaystyle{ n }[/math] tokens) than a direct representation by the corresponding count of a single token (with [math]\displaystyle{ n }[/math] tokens). This number system is used extensively in computing.[citation needed]
In a Euclidean space of any dimension greater than zero, two distinct points in a plane are always sufficient to define a unique line.[citation needed]
Powers of 2
Two is the first Mersenne prime exponent, and it is the difference between the first two Fermat primes (3 and 5). Powers of two are essential in computer science, and important in the constructability of regular polygons using basic tools (e.g., through the use of Fermat or Pierpont primes).
[math]\displaystyle{ 2 }[/math] is the only number such that the sum of the reciprocals of its natural powers equals itself. In symbols,
- [math]\displaystyle{ \sum_{n=0}^{\infin}\frac {1}{2^n}=1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\cdots=2. }[/math]
Two also has the unique property that [math]\displaystyle{ 2+2=2\times2=2^{2}=2\uparrow\uparrow 2= 2\uparrow\uparrow\uparrow2=\text{ }... }[/math] up through any level of hyperoperation, here denoted in Knuth's up-arrow notation, all equivalent to [math]\displaystyle{ 4. }[/math]
Notably, row sums in Pascal's triangle are in equivalence with successive powers of two, [math]\displaystyle{ 2^{n}. }[/math][7][8]
Properties
The numbers two and three are the only two consecutive prime numbers. Two is the first prime number that does not have a proper twin prime with a difference two, while three is the first such prime number to have a twin prime, five.[9][10] In consequence, three and five encase four in-between, which is the square of two, [math]\displaystyle{ 2^2 }[/math]. These are also the two odd prime numbers that lie amongst the only all-Harshad numbers (1, 2, 4, and 6)[11] that are also the first four highly composite numbers,[12] with 2 the only number that is both a prime number and a highly composite number.
Furthermore, [math]\displaystyle{ (3,5) }[/math] are the unique pair of twin primes [math]\displaystyle{ (q, q+2) }[/math] that yield the second and only prime quadruplet [math]\displaystyle{ (11, 13, 17, 19) }[/math] that is of the form [math]\displaystyle{ (d-4, d-2, d+2, d+4) }[/math], where [math]\displaystyle{ d }[/math] is the product of said twin primes.[13]
In particular, the sum of the reciprocals of all non-zero triangular numbers converges to 2.[14]
Integer sequences
The first number to return zero for the Mertens function is 2,[15] and the harmonic mean of the divisors of 6, the smallest Ore number greater than 1, is also 2.
Inside other important integer sequences, Template:Bullet list
Two consecutive twos (as in "22" for "two twos"), or equivalently "2-2", is the only fixed point of John Conway's look-and-say function.[16] On the other hand, there are no [math]\displaystyle{ 2\times2 }[/math] magic squares, and as such they are the only null [math]\displaystyle{ n }[/math] by [math]\displaystyle{ n }[/math] magic square set.[17][lower-alpha 1]
There are only two known sublime numbers, which are numbers with a perfect number of factors, whose sum itself yields a perfect number. 12 is one of the two sublime numbers, with the other being 76 digits long.[18]
Euler's number
[math]\displaystyle{ e }[/math] can be simplified to equal,
[math]\displaystyle{ e = \sum\limits_{n = 0}^{\infty} \frac{1}{n!} = 2 + \frac{1}{1\cdot 2} + \frac{1}{1\cdot 2\cdot 3} + \cdots }[/math]
A continued fraction for [math]\displaystyle{ e = [2; 1, 2, 1, 1, 4, 1, 1, 8, ...] }[/math] repeats a [math]\displaystyle{ \{1, 2n, 1\} }[/math] pattern from the second term onward.[19][20]
Geometry
Regarding regular polygons in two dimensions:
- The equilateral triangle has the smallest ratio of the circumradius [math]\displaystyle{ R }[/math] to the inradius [math]\displaystyle{ r }[/math] of any triangle by Euler's inequality, with [math]\displaystyle{ \tfrac{R}{r}=2. }[/math][21]
- The long diagonal of a regular hexagon is of length 2 when its sides are of unit length.[citation needed]
- The span of an octagon is in silver ratio [math]\displaystyle{ \delta_s }[/math] with its sides, which can be computed with the continued fraction [math]\displaystyle{ [2;2,2,...] = 2.414\;235\dots }[/math][22]
Whereas a square of unit side length has a diagonal equal to [math]\displaystyle{ \sqrt{2} }[/math], a space diagonal inside a tesseract measures 2 when its side lengths are of unit length.[citation needed]
A digon is a polygon with two sides (or edges) and two vertices. On a circle, it is a tessellation with two antipodal points and 180° arc edges.[citation needed]
For any polyhedron homeomorphic to a sphere, the Euler characteristic is [math]\displaystyle{ \chi=V-E+F=2 }[/math], where [math]\displaystyle{ V }[/math] is the number of vertices, [math]\displaystyle{ E }[/math] is the number of edges, and [math]\displaystyle{ F }[/math] is the number of faces. A double torus has an Euler characteristic of [math]\displaystyle{ -2 }[/math], on the other hand, and a non-orientable surface of like genus [math]\displaystyle{ k }[/math] has a characteristic [math]\displaystyle{ \chi=2-k }[/math].[citation needed]
The simplest tessellation in two-dimensional space, though an improper tessellation, is that of two [math]\displaystyle{ \infty }[/math]-sided apeirogons joined along all their edges, coincident about a line that divides the plane in two. This order-2 apeirogonal tiling is the arithmetic limit of the family of dihedra [math]\displaystyle{ \{p, 2\} }[/math].[citation needed]
List of basic calculations
| Multiplication | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 50 | 100 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 × x | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 32 | 34 | 36 | 38 | 40 | 42 | 44 | 46 | 48 | 50 | 100 | 200 |
| Division | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2 ÷ x | 2 | 1 | 0.6 | 0.5 | 0.4 | 0.3 | 0.285714 | 0.25 | 0.2 | 0.2 | 0.18 | 0.16 | 0.153846 | 0.142857 | 0.13 | 0.125 | 0.1176470588235294 | 0.1 | 0.105263157894736842 | 0.1 | |
| x ÷ 2 | 0.5 | 1.5 | 2 | 2.5 | 3 | 3.5 | 4 | 4.5 | 5 | 5.5 | 6 | 6.5 | 7 | 7.5 | 8 | 8.5 | 9 | 9.5 | 10 |
| Exponentiation | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 2x | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | 512 | 1024 | 2048 | 4096 | 8192 | 16384 | 32768 | 65536 | 131072 | 262144 | 524288 | 1048576 | |
| x2 | 1 | 9 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 | 256 | 289 | 324 | 361 | 400 |
In science
- The number of polynucleotide strands in a DNA double helix.[23]
- The first magic number.[24]
- The atomic number of helium.[25]
See also
- List of highways numbered 2
- Binary number
Notes
- ↑ Meanwhile, the magic constant of an [math]\displaystyle{ n }[/math]-pointed normal magic star is [math]\displaystyle{ M = 4n + 2 }[/math].
References
- ↑ Georges Ifrah, The Universal History of Numbers: From Prehistory to the Invention of the Computer transl. David Bellos et al. London: The Harvill Press (1998): 393, Fig. 24.62
- ↑ Huddleston, Rodney D.; Pullum, Geoffrey K.; Reynolds, Brett (2022). A student's introduction to English grammar (2nd ed.). Cambridge, United Kingdom: Cambridge University Press. pp. 117. ISBN 978-1-316-51464-1. OCLC 1255524478. https://www.worldcat.org/oclc/1255524478.
- ↑ 3.0 3.1 two, adj., n., and adv. (3rd ed.), Oxford University Press, September 2005, http://oed.com/search?searchType=dictionary&q=two%2C+adj.%2C+n.%2C+and+adv. (Subscription or UK public library membership required.)
- ↑ "Sloane's A002378: Pronic numbers". OEIS Foundation. https://oeis.org/A002378.
- ↑ Sloane, N. J. A., ed. "Sequence A005843 (The nonnegative even numbers)". OEIS Foundation. https://oeis.org/A005843. Retrieved 2022-12-15.
- ↑ Hardy, G. H.; Wright, E. M. (2008), An Introduction to the Theory of Numbers, Revised by D. R. Heath-Brown and J. H. Silverman. Foreword by Andrew Wiles. (6th ed.), Oxford: Oxford University Press, pp. 342–347, §18.1, ISBN 978-0-19-921986-5
- Also, [math]\displaystyle{ \limsup_{n\to\infty}\frac{\log d(n)}{\log n/\log\log n} = \log 2 }[/math].
- ↑ Smith, Karl J. (1973). "Pascal's Triangle". The Two-Year College Mathematics Journal (Washington, D.C.: Mathematical Association of America) 4 (1): 4. doi:10.1080/00494925.1973.11974228. https://www.jstor.org/stable/2698949.
- ↑ Sloane, N. J. A., ed. "Sequence A000079 (Powers of 2: a(n) equal to 2^n.)". OEIS Foundation. https://oeis.org/A000079. Retrieved 2023-01-06.
- ↑ Sloane, N. J. A., ed. "Sequence A007510 (Single (or isolated or non-twin) primes: Primes p such that neither p-2 nor p+2 is prime.)". OEIS Foundation. https://oeis.org/A007510. Retrieved 2022-12-05.
- ↑ Sloane, N. J. A., ed. "Sequence A001359 (Lesser of twin primes.)". OEIS Foundation. https://oeis.org/A001359. Retrieved 2022-12-05.
- ↑ PrimeFan (2013-03-22). "Harshad number". https://planetmath.org/harshadnumber.
- ↑ Sloane, N. J. A., ed. "Sequence A002182 (Highly composite numbers, definition (1): numbers n where d(n), the number of divisors of n (A000005), increases to a record.)". OEIS Foundation. https://oeis.org/A002182. Retrieved 2023-12-18.
- ↑ Sloane, N. J. A., ed. "Sequence A136162 (List of prime quadruplets {p, p+2, p+6, p+8}.)". OEIS Foundation. https://oeis.org/A136162. Retrieved 2023-06-09.
- "{11, 13, 17, 19} is the only prime quadruplet {p, p+2, p+6, p+8} of the form {Q-4, Q-2, Q+2, Q+4} where Q is a product of a pair of twin primes {q, q+2} (for prime q = 3) because numbers Q-2 and Q+4 are for q>3 composites of the form 3*(12*k^2-1) and 3*(12*k^2+1) respectively (k is an integer)."
- ↑ Grabowski, Adam (2013). "Polygonal numbers". Formalized Mathematics (Sciendo (De Gruyter)) 21 (2): 103–113. doi:10.2478/forma-2013-0012.
- ↑ Sloane, N. J. A., ed. "Sequence A028442 (Numbers k such that Mertens's function M(k) (A002321) is zero.)". OEIS Foundation. https://oeis.org/A028442. Retrieved 2023-09-02.
- ↑ Martin, Oscar (2006). "Look-and-Say Biochemistry: Exponential RNA and Multistranded DNA". American Mathematical Monthly (Mathematical association of America) 113 (4): 289–307. doi:10.2307/27641915. ISSN 0002-9890. http://www.uam.es/personal_pdi/ciencias/omartin/Biochem.PDF. Retrieved 2022-07-21.
- ↑ Sloane, N. J. A., ed. "Sequence A006052 (Number of magic squares of order n composed of the numbers from 1 to n^2, counted up to rotations and reflections.)". OEIS Foundation. https://oeis.org/A006052. Retrieved 2022-07-21.
- ↑ Sloane, N. J. A., ed. "Sequence A081357 (Sublime numbers)". OEIS Foundation. https://oeis.org/A081357. Retrieved 2022-07-13.
- ↑ Cohn, Henry (2006). "A Short Proof of the Simple Continued Fraction Expansion of e". The American Mathematical Monthly (Taylor & Francis, Ltd.) 113 (1): 57–62. doi:10.1080/00029890.2006.11920278. https://www.jstor.org/stable/27641837. Retrieved 2023-04-30.
- ↑ Sloane, N. J. A., ed. "Sequence A005131 (A generalized continued fraction for Euler's number e.)". OEIS Foundation. https://oeis.org/A005131. Retrieved 2023-04-30.
- "Only a(1) = 0 prevents this from being a simple continued fraction. The motivation for this alternate representation is that the simple pattern {1, 2*n, 1} (from n=0) may be more mathematically appealing than the pattern in the corresponding simple continued fraction (at A003417)."
- ↑ Svrtan, Dragutin; Veljan, Darko (2012). "Non-Euclidean versions of some classical triangle inequalities". Forum Geometricorum (Boca Raton, FL: Department of Mathematical Sciences, Florida Atlantic University) 12: 198. ISSN 1534-1178. http://forumgeom.fau.edu/FG2012volume12/FG201217.pdf. Retrieved 2023-04-30.
- ↑ Vera W. de Spinadel (1999). "The Family of Metallic Means". Visual Mathematics (Belgrade: Mathematical Institute of the Serbian Academy of Sciences) 1 (3). http://www.mi.sanu.ac.rs/vismath/spinadel/index.html. Retrieved 2023-02-25.
- ↑ "Double-stranded DNA". Scitable. Nature Education. https://www.nature.com/scitable/content/double-stranded-dna-6834149/.
- ↑ "The Complete Explanation of the Nuclear Magic Numbers Which Indicate the Filling of Nucleonic Shells and the Revelation of Special Numbers Indicating the Filling of Subshells Within Those Shells". https://www.sjsu.edu/faculty/watkins/magicnumbers2.htm.
- ↑ Bezdenezhnyi, V. P. (2004). "Nuclear Isotopes and Magic Numbers". Odessa Astronomical Publications 17: 11. Bibcode: 2004OAP....17...11B.
External links
| Wikimedia Commons has media related to: |
 |