Astronomy:Equivalence principle

From HandWiki
Revision as of 05:37, 6 February 2024 by Rtextdoc (talk | contribs) (linkage)
(diff) ← Older revision | Latest revision (diff) | Newer revision → (diff)
Short description: The hypothesis that inertial and gravitational masses are equivalent
A falling object behaves exactly the same on a planet or in an equivalent accelerating frame of reference.
General relativity
Spacetime curvature schematic
[math]\displaystyle{ G_{\mu \nu} + \Lambda g_{\mu \nu}= {\kappa} T_{\mu \nu} }[/math]
Fundamental concepts
Phenomena
Spacetime

The equivalence principle is the hypothesis that the observed equivalence of gravitational and inertial mass is a consequence of nature. The weak form, known for centuries, relates to masses of any composition in free fall taking the same trajectories and landing at identical times. The extended form by Albert Einstein requires special relativity to also hold in free fall and requires the weak equivalence to be valid everywhere. This form was a critical input for the development of the theory of general relativity. The strong form requires Einstein's form to work for stellar objects. Highly precise experimental tests of the principle limit possible deviations from equivalence to very small.

Concept

In classical mechanics, Newton's equation of motion in a gravitational field, written out in full, is:

inertial mass × acceleration = gravitational mass × intensity of the gravitational field

Here, the inertial mass is the intrinsic 'resistance' to acceleration, the kind of resistance feel from trying to push a car by hand. Gravitational mass of the car is its response to the gravitational field.[1]:32

Very careful experiments have shown that the inertial mass on the left side and gravitational mass on the right side are numerically equal and independent of the material composing the masses. The equivalence principle is the hypothesis that this numerical equality of inertial and gravitational mass is a consequence of their fundamental identity.[1]:32

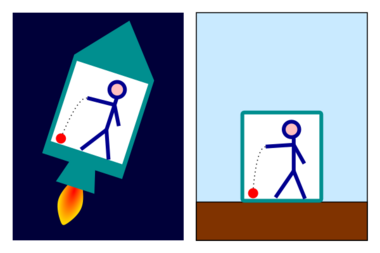
The equivalence principle can be considered an extension of the principle of relativity, the principle that the laws of physics are invariant under uniform motion. An observer in a windowless room cannot distinguish between being on the surface of the Earth and being in a spaceship in deep space accelerating at 1g and the laws of physics are unable to distinguish these cases.[1]:33

History

The concept that two unequal masses fall at the same rate in Earth's gravity was known to Aristotle; Galileo compared different materials experimentally to determine that the acceleration due to gravitation is independent of the amount of mass being accelerated.[2]

Johannes Kepler, using Galileo's discoveries, showed knowledge of the equivalence principle by accurately describing what would occur if the Moon were stopped in its orbit and dropped towards Earth. This can be deduced without knowing if or in what manner gravity decreases with distance, but requires assuming the equivalency between gravity and inertia.

If two stones were placed in any part of the world near each other, and beyond the sphere of influence of a third cognate body, these stones, like two magnetic needles, would come together in the intermediate point, each approaching the other by a space proportional to the comparative mass of the other. If the moon and earth were not retained in their orbits by their animal force or some other equivalent, the earth would mount to the moon by a fifty-fourth part of their distance, and the moon fall towards the earth through the other fifty-three parts, and they would there meet, assuming, however, that the substance of both is of the same density.
—Johannes Kepler, "Astronomia Nova", 1609[3]

The 1/54 ratio is Kepler's estimate of the Moon–Earth mass ratio, based on their diameters. The accuracy of his statement can be deduced by using Newton's inertia law F=ma and Galileo's gravitational observation that distance D = at2/2. Setting these accelerations equal for a mass is the equivalence principle. Noting the time to collision for each mass is the same gives Kepler's statement that: [math]\displaystyle{ \frac{D_\text{Moon}}{D_\text{Earth}} = \frac{M_\text{Moon}}{M_\text{Earth}} }[/math] without knowing the time to collision or how or if the acceleration force from gravity is a function of distance.

Newton, just 50 years after Galileo, developed the idea that gravitational and inertial mass were different concepts and compared the periods of pendulums composed of different materials to verify that these masses are the same. This form of the equivalence principle became known as "weak equivalence".[2]

A version of the equivalence principle consistent with special relativity was introduced by Albert Einstein in 1907, when he observed that identical physical laws are observed in two systems, one subject to a constant gravitational field causing acceleration and the other subject to constant acceleration like a rocket far from any gravitational field.[4]:152 Since the physical laws are the same, Einstein assumed the graviational field and the acceleration were "physically equivalent". Einstein stated this hypothesis as:

we ... assume the complete physical equivalence of a gravitational field and a corresponding acceleration of the reference system.
—Einstein, 1907[5]

In 1911 Einstein demonstrated the power of the equivalence principle by using it to predict that clocks run at different rates in a gravitational potential, and light rays bend in a gravitational field.[4]:153 He connected the equivalence principle to his earlier principle of special relativity:

This assumption of exact physical equivalence makes it impossible for us to speak of the absolute acceleration of the system of reference, just as the usual theory of relativity forbids us to talk of the absolute velocity of a system; and it makes the equal falling of all bodies in a gravitational field seem a matter of course.
—Einstein, 1911[6]

Immediately after completing his work[7]:111 on a theory of gravity (known as general relativity) and in later years Einstein recalled the role of the equivalence principle:

The breakthrough came suddenly one day. I was sitting on a chair in my patent office in Bern. Suddenly a thought struck me: If a man falls freely, he would not feel his weight. I was taken aback. This simple thought experiment made a deep impression on me. This led me to the theory of gravity.
— Einstein, 1922[8]

Since Einstein developed general relativity, there was a need to develop a framework to test the theory against other possible theories of gravity compatible with special relativity. This was developed by Robert Dicke as part of his program to test general relativity. Two new principles were suggested, the so-called Einstein equivalence principle and the strong equivalence principle, each of which assumes the weak equivalence principle as a starting point. These are discussed below.

Definitions

File:Apollo 15 feather and hammer drop.ogvThree main forms of the equivalence principle are in current use: weak (Galilean), Einsteinian, and strong.[9]:6 Some studies also create finer divisions or slight alternative.[10][11]

Weak equivalence principle

The weak equivalence principle, also known as the universality of free fall or the Galilean equivalence principle can be stated in many ways. The strong equivalence principle, a generalization of the weak equivalence principle, includes astronomic bodies with gravitational self-binding energy.[12] Instead, the weak equivalence principle assumes falling bodies are self-bound by non-gravitational forces only (e.g. a stone). Either way:

  • "All uncharged, freely falling test particles follow the same trajectories, once an initial position and velocity have been prescribed".[9]:6
  • "... in a uniform gravitational field all objects, regardless of their composition, fall with precisely the same acceleration." "The weak equivalence principle implicitly assumes that the falling objects are bound by non-gravitational forces."[12]
  • "... in a gravitational field the acceleration of a test particle is independent of its properties, including its rest mass."[13]
  • Mass (measured with a balance) and weight (measured with a scale) are locally in identical ratio for all bodies (the opening page to Newton's Philosophiæ Naturalis Principia Mathematica, 1687).

Uniformity of the gravitational field eliminates measurable tidal forces originating from a radial divergent gravitational field (e.g., the Earth) upon finite sized physical bodies.

Einstein equivalence principle

What is now called the "Einstein equivalence principle" states that the weak equivalence principle holds, and that:

the outcome of any local, non-gravitational test experiment is independent of the experimental apparatus’ velocity relative to the gravitational field and is independent of where and when in the gravitational field the experiment is performed.[14]

Here local means that experimental setup must be small compared to variations in the gravitational field, called tidal forces. The test experiment must be small enough so that its gravitational potential does not alter the result.

The two additional constraints added to the weak principle to get the Einstein form − (1) the independence of the outcome on relative velocity (local Lorentz invariance) and (2) independence of "where" known as (local positional invariance) − have far reaching consequences. With these constraints alone Einstein was able to predict the gravitational redshift.[14] Theories of gravity that obey the Einstein equivalence principle must be "metric theories", meaning that trajectories of freely falling bodies are geodesics of symmetric metric.[15]:9

Around 1960 Leonard I. Schiff conjectured that any complete and consistent theory of gravity the embodies the weak equivalence principle implies the Einstein equivalence principle; the conjecture can't be proven but has several plausibility arguments in its favor.[15]:20 Nonetheless, the two principles are tested with very different kinds of experiments.

The Einstein equivalence principle has been criticized as imprecise, because there is no universally accepted way to distinguish gravitational from non-gravitational experiments (see for instance Hadley[16] and Durand[17]).

Strong equivalence principle

The strong equivalence principle applies the same constraints as the Einstein equivalence principle, but allows the freely falling bodies to be massive gravitating objects as well as test particles.[9] Thus this is a version of the equivalence principle that applies to objects that exert a gravitational force on themselves, such as stars, planets, black holes or Cavendish experiments. It requires that the gravitational constant be the same everywhere in the universe[15]:49 and is incompatible with a fifth force. It is much more restrictive than the Einstein equivalence principle.

Like the Einstein equivalence principle, the strong equivalence principle requires gravity is geometrical by nature, but in addition it forbids any extra fields, so the metric alone determines all of the effects of gravity. If an observer measures a patch of space to be flat, then the strong equivalence principle suggests that it is absolutely equivalent to any other patch of flat space elsewhere in the universe. Einstein's theory of general relativity (including the cosmological constant) is thought to be the only theory of gravity that satisfies the strong equivalence principle. A number of alternative theories, such as Brans–Dicke theory and the Einstein-aether theory add additional fields.[9]

Active, passive, and inertial masses

Some of the tests of the equivalence principle use names for the different ways mass appears in physical formulae. In nonrelativistic physics three kinds of mass can be distinguished:[15]

  1. Inertial mass intrinsic to an object, the sum of all of its mass–energy.
  2. Passive mass, the response to gravity, the object's weight.
  3. Active mass, the mass that determines the objects gravitational effect.

By definition of active and passive gravitational mass, the force on [math]\displaystyle{ M_1 }[/math] due to the gravitational field of [math]\displaystyle{ M_0 }[/math] is: [math]\displaystyle{ F_1 = \frac{M_0^\mathrm{act} M_1^\mathrm{pass}}{r^2} }[/math] Likewise the force on a second object of arbitrary mass2 due to the gravitational field of mass0 is: [math]\displaystyle{ F_2 = \frac{M_0^\mathrm{act} M_2^\mathrm{pass}}{r^2} }[/math]

By definition of inertial mass:[math]\displaystyle{ F = m^\mathrm{inert} a }[/math]if [math]\displaystyle{ m_1 }[/math] and [math]\displaystyle{ m_2 }[/math] are the same distance [math]\displaystyle{ r }[/math] from [math]\displaystyle{ m_0 }[/math] then, by the weak equivalence principle, they fall at the same rate (i.e. their accelerations are the same). [math]\displaystyle{ a_1 = \frac{F_1}{m_1^\mathrm{inert}} = a_2 = \frac{F_2}{m_2^\mathrm{inert}} }[/math]

Hence: [math]\displaystyle{ \frac{M_0^\mathrm{act} M_1^\mathrm{pass}}{r^2 m_1^\mathrm{inert}} = \frac{M_0^\mathrm{act} M_2^\mathrm{pass}}{r^2 m_2^\mathrm{inert}} }[/math]

Therefore: [math]\displaystyle{ \frac{M_1^\mathrm{pass}}{m_1^\mathrm{inert}} = \frac{M_2^\mathrm{pass}}{m_2^\mathrm{inert}} }[/math]

In other words, passive gravitational mass must be proportional to inertial mass for objects, independent of their material composition if the weak equivalence principle is obeyed.

The dimensionless Eötvös-parameter or Eötvös ratio [math]\displaystyle{ \eta(A,B) }[/math] is the difference of the ratios of gravitational and inertial masses divided by their average for the two sets of test masses "A" and "B". [math]\displaystyle{ \eta(A,B)=2\frac{ \left(\frac{m_{\textrm pass}}{m_{\textrm inert}}\right)_A-\left(\frac{m_{\textrm pass}}{m_{\textrm inert}}\right)_B }{\left(\frac{m_{\textrm pass}}{m_{\textrm inert}}\right)_A+\left(\frac{m_{\textrm pass}}{m_{\textrm inert}}\right)_B}. }[/math] Values of this parameter are used to compare tests of the equivalence principle.[15]:10

A similar parameter can be used to compare passive and active mass. By Newton's third law of motion: [math]\displaystyle{ F_1 = \frac{M_0^\mathrm{act} M_1^\mathrm{pass}}{r^2} }[/math] must be equal and opposite to [math]\displaystyle{ F_0 = \frac{M_1^\mathrm{act} M_0^\mathrm{pass}}{r^2} }[/math]

It follows that: [math]\displaystyle{ \frac{M_0^\mathrm{act}}{M_0^\mathrm{pass}} = \frac{M_1^\mathrm{act}}{M_1^\mathrm{pass}} }[/math]

In words, passive gravitational mass must be proportional to active gravitational mass for all objects. The difference, [math]\displaystyle{ S_{0,1} = \frac{M_0^\mathrm{act}}{M_0^\mathrm{pass}} - \frac{M_1^\mathrm{act}}{M_1^\mathrm{pass}} }[/math] is used to quantify differences between passive and active mass.[18]

Experimental tests

Tests of the weak equivalence principle

Tests of the weak equivalence principle are those that verify the equivalence of gravitational mass and inertial mass. An obvious test is dropping different objects and verifying that they land at the same time. Historically this was the first approach, though probably not by Galileo's Leaning Tower of Pisa experiment[19]:19–21 but earlier by Simon Stevin[20] who dropped lead balls of different masses off the Delft churchtower and listened for the sound they made on a wooden plank.

Isaac Newton measured the period of pendulums made with different materials as an alternative test giving the first precision measurements.[2] Loránd Eötvös's approach in 1908 used a very sensitive torsion balance to give precision approaching 1 in a billion. Modern experiments have improved this by another factor of a million.

A popular exposition of this measurement was done on the Moon by David Scott in 1971. He dropped a falcon feather and a hammer at the same time, showing on video[21] that they landed at the same time.

Chronology of weak equivalence principles tests[22]
Year Investigator Sensitivity Method
500? John Philoponus[23] "small" Drop tower
1585 Simon Stevin[24][20] 5×10−2 Drop tower
1590? Galileo Galilei[25][22]:91 2×10−3 Pendulum, drop tower
1686 Isaac Newton[26][22]:91 10−3 Pendulum
1832 Friedrich Wilhelm Bessel[27][22]:91 2×10−5 Pendulum
1908 (1922) Loránd Eötvös[28][22]:92 2×10−9 Torsion balance
1910 Southerns[29][22]:91 5×10−6 Pendulum
1918 Zeeman[30][22]:91 3×10−8 Torsion balance
1923 Potter[31][22]:91 3×10−6 Pendulum
1935 Renner[32][22]:92 2×10−9 Torsion balance
1964 Roll, Krotkov, Dicke[33] 3×10−11 Torsion balance
1972 Braginsky, Panov[34][22]:92 10−12 Torsion balance
1976 Shapiro, et al.[35][22]:92 10−12 Lunar laser ranging
1979 Keiser, Faller[36][22]:93 4×10−11 Fluid support
1987 Niebauer, et al.[37][22]:95 10−10 Drop tower
1989 Stubbs, et al.[38][22]:93 10−11 Torsion balance
1990 Adelberger, Eric G.; et al.[39][22]:95 10−12 Torsion balance
1999 Baessler, et al.[40][41] 5×10−14 Torsion balance
2008 Schlamminger, et al.[42] 10−13 Torsion balance
2017 MICROSCOPE[43][44] 10−15 Earth orbit

Experiments are still being performed at the University of Washington which have placed limits on the differential acceleration of objects towards the Earth, the Sun and towards dark matter in the Galactic Center.[45] Future satellite experiments[46] – Satellite Test of the Equivalence Principle[47] and Galileo Galilei – will test the weak equivalence principle in space, to much higher accuracy.[48]

With the first successful production of antimatter, in particular anti-hydrogen, a new approach to test the weak equivalence principle has been proposed. Experiments to compare the gravitational behavior of matter and antimatter are currently being developed.[49]

Proposals that may lead to a quantum theory of gravity such as string theory and loop quantum gravity predict violations of the weak equivalence principle because they contain many light scalar fields with long Compton wavelengths, which should generate fifth forces and variation of the fundamental constants. Heuristic arguments suggest that the magnitude of these equivalence principle violations could be in the 10−13 to 10−18 range.[50]

Currently envisioned tests of the weak equivalence principle are approaching a degree of sensitivity such that non-discovery of a violation would be just as profound a result as discovery of a violation. Non-discovery of equivalence principle violation in this range would suggest that gravity is so fundamentally different from other forces as to require a major reevaluation of current attempts to unify gravity with the other forces of nature. A positive detection, on the other hand, would provide a major guidepost towards unification.[50]

Tests of the Einstein equivalence principle

In addition to the tests of the weak equivalence principle, the Einstein equivalence principle requires testing the local Lorentz invariance and local positional invariance conditions.

Testing local Lorentz invariance amounts to testing special relativity, a theory with vast number of existing tests.[15]:12 Nevertheless, attempts to look for quantum gravity require even more precise tests. The modern tests include looking for directional variations in the speed of light (called "clock anisotropy tests") and new forms of the Michelson-Morley experiment. The anisotropy measures less than one part in 10−20.[15]:14

Testing local positional invariance divides in to tests in space and in time.[15]:17 Space-based tests use measurements of the gravitational redshift, the classic is the Pound–Rebka experiment in the 1960s. The most precise measurement was done in 1976 by flying a hydrogen maser and comparing it to one on the ground. The Global positioning system requires compensation for this redshift to give accurate position values.

Time-based tests search for variation of dimensionless constants and mass ratios.[51] For example, Webb et al.[52] reported detection of variation (at the 10−5 level) of the fine-structure constant from measurements of distant quasars. Other researchers dispute these findings.[53]

The present best limits on the variation of the fundamental constants have mainly been set by studying the naturally occurring Oklo natural nuclear fission reactor, where nuclear reactions similar to ones we observe today have been shown to have occurred underground approximately two billion years ago. These reactions are extremely sensitive to the values of the fundamental constants.

Tests of changes in fundamental constants[15]:19
Constant Year Method Limit on fractional change per year
weak interaction constant 1976 Oklo 10−11
fine-structure constant 1976 Oklo 10−16
electron–proton mass ratio 2002 quasars 10−15

Tests of the strong equivalence principle

The strong equivalence principle can be tested by 1) finding orbital variations in massive bodies (Sun-Earth-Moon), 2 )variations in the gravitational constant (G) depending on nearby sources of gravity or on motion, or 3) searching for a variation of Newton's gravitational constant over the life of the universe[15]:47

Orbital variations due to gravitational self-energy should cause a "polarization" of solar system orbits called the Nordtvedt effect. This effect has been sensitively tested by the Lunar Laser Ranging Experiment.[54][55] Up to the limit of one part in 1013 there is no Nordtvedt effect.

A tight bound on the effect of nearby gravitational fields on the strong equivalence principle comes from modeling the orbits of binary stars and comparing the results to pulsar timing data.[15]:49 In 2014, astronomers discovered a stellar triple system containing a millisecond pulsar PSR J0337+1715 and two white dwarfs orbiting it. The system provided them a chance to test the strong equivalence principle in a strong gravitational field with high accuracy.[56][57][58][59]

Most alternative theories of gravity predict a change in the gravity constant over time. Studies of Big Bang nucleosynthesis, analysis of pulsars, and the lunar laser ranging data have shown that G cannot have varied by more than 10% since the creation of the universe. The best data comes from studies of the ephemeris of Mars, based on three successive NASA missions, Mars Global Surveyor, Mars Odyssey, and Mars Reconnaissance Orbiter.[15]:50

See also


References

  1. ↑ 1.0 1.1 1.2 Einstein, Albert (2003). The Meaning of Relativity. Routledge. p. 59. ISBN 9781134449798. https://archive.org/details/meaningrelativit00aein. 
  2. ↑ 2.0 2.1 2.2 Everitt, C.W.F.; Damour, T.; Nordtvedt, K.; Reinhard, R. (October 2003). "Historical perspective on testing the Equivalence Principle" (in en). Advances in Space Research 32 (7): 1297–1300. doi:10.1016/S0273-1177(03)90335-8. Bibcode: 2003AdSpR..32.1297E. https://linkinghub.elsevier.com/retrieve/pii/S0273117703903358. 
  3. ↑ John Elliot Drinkwater Bethune (1832). Life of Galileo Galilei: With Illustrations of the Advancement of Experimental Philosophy. W. Hyde. p. 201. https://books.google.com/books?id=oECwXhOJ0ZYC.  Extract of page 201
  4. ↑ 4.0 4.1 Whittaker, Sir Edmund (1989-01-01). A History of the Theories of Aether and Electricity. 2. Courier Dover Publications. ISBN 0-486-26126-3. 
  5. ↑ Einstein, Albert. "On the relativity principle and the conclusions drawn from it." Jahrb Radioaktivitat Elektronik 4 (1907): 411–462.
  6. ↑ Einstein, Albert. "On the Influence of Gravitation on the Propagation of Light." Annalen der Physik 35.898–908 (1911): 906.
  7. ↑ Lorentz, Hendrik Antoon, et al. The Principle of Relativity: A Collection of Original Memoirs on the Special and General Theory of Relativity. United Kingdom, Dover Publications, 1923.
  8. ↑ Einstein, Albert, How I Constructed the Theory of Relativity, translated by Masahiro Morikawa from the text recorded in Japanese by Jun Ishiwara, Association of Asia Pacific Physical Societies (AAPPS) Bulletin, Vol. 15, No. 2, pp. 17–19, April 2005. Einstein recalls events of 1907 in a talk in Japan on 14 December 1922.
  9. ↑ 9.0 9.1 9.2 9.3 Clifton, Timothy; Ferreira, Pedro G.; Padilla, Antonio; Skordis, Constantinos (March 2012). "Modified gravity and cosmology" (in en). Physics Reports 513 (1–3): 1–189. doi:10.1016/j.physrep.2012.01.001. Bibcode: 2012PhR...513....1C. https://linkinghub.elsevier.com/retrieve/pii/S0370157312000105. 
  10. ↑ Di Casola, Eolo; Liberati, Stefano; Sonego, Sebastiano (2015-01-01). "Nonequivalence of equivalence principles" (in en). American Journal of Physics 83 (1): 39–46. doi:10.1119/1.4895342. ISSN 0002-9505. Bibcode: 2015AmJPh..83...39D. https://pubs.aip.org/ajp/article/83/1/39/1042100/Nonequivalence-of-equivalence-principles. "We have seen that the various formulations of the equivalence principle form hierarchy (or rather, a nested sequence of statements narrowing down the type of gravitational theory),". 
  11. ↑ Ghins, Michel; Budden, Tim (March 2001). "The Principle of Equivalence" (in en). Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics 32 (1): 33–51. doi:10.1016/S1355-2198(00)00038-1. Bibcode: 2001SHPMP..32...33G. https://linkinghub.elsevier.com/retrieve/pii/S1355219800000381. 
  12. ↑ 12.0 12.1 Wagner, Todd A.; Schlamminger, Stephan; Gundlach, Jens H.; Adelberger, Eric G. (2012). "Torsion-balance tests of the weak equivalence principle". Classical and Quantum Gravity 29 (18): 184002. doi:10.1088/0264-9381/29/18/184002. Bibcode: 2012CQGra..29r4002W. 
  13. ↑ Wesson, Paul S. (2006). Five-dimensional Physics. World Scientific. p. 82. ISBN 978-981-256-661-4. https://books.google.com/books?id=dSv8ksxHR0oC&q=intitle:Five+intitle:Dimensional+intitle:Physics. 
  14. ↑ 14.0 14.1 Haugen, Mark P.; Lämmerzahl, Claus (2001). "Principles of Equivalence: Their Role in Gravitation Physics and Experiments That Test Them.". Gyros, Clocks, Interferometers...: Testing Relativistic Graviy in Space. Lecture Notes in Physics. 562. pp. 195–212. doi:10.1007/3-540-40988-2_10. ISBN 978-3-540-41236-6. Bibcode: 2001LNP...562..195H. 
  15. ↑ 15.00 15.01 15.02 15.03 15.04 15.05 15.06 15.07 15.08 15.09 15.10 15.11 Will, Clifford M. (Dec 2014). "The Confrontation between General Relativity and Experiment" (in en). Living Reviews in Relativity 17 (1): 4. doi:10.12942/lrr-2014-4. ISSN 2367-3613. PMID 28179848. Bibcode: 2014LRR....17....4W. 
  16. ↑ Hadley, Mark J. (1997). "The Logic of Quantum Mechanics Derived from Classical General Relativity". Foundations of Physics Letters 10 (1): 43–60. doi:10.1007/BF02764119. Bibcode: 1997FoPhL..10...43H. 
  17. ↑ Durand, Stéphane (2002). "An amusing analogy: modelling quantum-type behaviours with wormhole-based time travel". Journal of Optics B: Quantum and Semiclassical Optics 4 (4): S351–S357. doi:10.1088/1464-4266/4/4/319. Bibcode: 2002JOptB...4S.351D. http://stacks.iop.org/ob/4/S351. 
  18. ↑ Singh, Vishwa Vijay; Müller, Jürgen; Biskupek, Liliane; Hackmann, Eva; Lämmerzahl, Claus (2023-07-13). "Equivalence of Active and Passive Gravitational Mass Tested with Lunar Laser Ranging" (in en). Physical Review Letters 131 (2): 021401. doi:10.1103/PhysRevLett.131.021401. ISSN 0031-9007. PMID 37505941. Bibcode: 2023PhRvL.131b1401S. https://link.aps.org/doi/10.1103/PhysRevLett.131.021401. 
  19. ↑ Drake, Stillman (2003). Galileo at Work: His Scientific Biography (Facsim. ed.). Mineola (N.Y.): Dover publ.. ISBN 9780486495422. 
  20. ↑ 20.0 20.1 Devreese, Jozef T.; Vanden Berghe, Guido (2008). 'Magic Is No Magic': The Wonderful World of Simon Stevin. WIT Press. p. 154. ISBN 9781845643911. https://books.google.com/books?isbn=1845643917. 
  21. ↑ "Weak Equivalence Principle test on the moon". https://www.youtube.com/watch?v=MJyUDpm9Kvk. 
  22. ↑ 22.00 22.01 22.02 22.03 22.04 22.05 22.06 22.07 22.08 22.09 22.10 22.11 22.12 22.13 22.14 Ciufolini, Ignazio; Wheeler, John A.; Gravitation and Inertia, Princeton, New Jersey: Princeton University Press, 1995, pp. 117–119
  23. ↑ Philoponus, John; "Corollaries on Place and Void", translated by David Furley, Ithaca, New York: Cornell University Press, 1987
  24. ↑ Stevin, Simon; De Beghinselen der Weeghconst ["Principles of the Art of Weighing"], Leyden, 1586; Dijksterhuis, Eduard J.; "The Principal Works of Simon Stevin", Amsterdam, 1955
  25. ↑ Galilei, Galileo; "Discorsi e Dimostrazioni Matematiche Intorno a Due Nuove Scienze", Leida: Appresso gli Elsevirii, 1638; "Discourses and Mathematical Demonstrations Concerning Two New Sciences", Leiden: Elsevier Press, 1638
  26. ↑ Newton, Isaac; "Philosophiae Naturalis Principia Mathematica" [Mathematical Principles of Natural Philosophy and his System of the World], translated by Andrew Motte, revised by Florian Cajori, Berkeley, California: University of California Press, 1934; Newton, Isaac; "The Principia: Mathematical Principles of Natural Philosophy", translated by I. Bernard Cohen and Anne Whitman, with the assistance of Julia Budenz, Berkeley, California: University of California Press, 1999
  27. ↑ Bessel, Friedrich W.; "Versuche Uber die Kraft, mit welcher die Erde Körper von verschiedner Beschaffenhelt anzieht", Annalen der Physik und Chemie, Berlin: J. Ch. Poggendorff, 25 401–408 (1832)
  28. ↑ R. v. Eötvös 1890 Mathematische und Naturwissenschaftliche Berichte aus Ungarn, 8, 65; Annalen der Physik (Leipzig) 68 11 (1922); Smith, G. L.; Hoyle, C. D.; Gundlach, J. H.; Adelberger, E. G.; Heckel, B. R.; Swanson, H. E. (1999). "Short-range tests of the equivalence principle". Physical Review D 61 (2): 022001. doi:10.1103/PhysRevD.61.022001. Bibcode: 1999PhRvD..61b2001S. 
  29. ↑ Southerns, Leonard (1910). "A Determination of the Ratio of Mass to Weight for a Radioactive Substance". Proceedings of the Royal Society of London 84 (571): 325–344. doi:10.1098/rspa.1910.0078. Bibcode: 1910RSPSA..84..325S. 
  30. ↑ Zeeman, Pieter (1918) "Some experiments on gravitation: The ratio of mass to weight for crystals and radioactive substances", Proceedings of the Koninklijke Nederlandse Akademie van Wetenschappen, Amsterdam 20(4) 542–553
  31. ↑ Potter, Harold H. (1923). "Some Experiments on the Proportionality of Mass and Weight". Proceedings of the Royal Society of London 104 (728): 588–610. doi:10.1098/rspa.1923.0130. Bibcode: 1923RSPSA.104..588P. 
  32. ↑ Renner, János (1935). "Kísérleti vizsgálatok a tömegvonzás és tehetetlenség arányosságáról". Mathematikai és Természettudományi Értesítő 53: 569. 
  33. ↑ Roll, Peter G.; Krotkov, Robert; Dicke, Robert H.; The equivalence of inertial and passive gravitational mass, Annals of Physics, Volume 26, Issue 3, 20 February 1964, pp. 442–517
  34. ↑ Braginski, Vladimir Borisovich; Panov, Vladimir Ivanovich (1971). "Журнал Экспериментальной и Теоретической Физики". (Zhurnal Éksperimental'noĭ I Teoreticheskoĭ Fiziki, Journal of Experimental and Theoretical Physics) 61: 873. 
  35. ↑ Shapiro, Irwin I.; Counselman, III; Charles, C.; King, Robert W. (1976). "Verification of the principle of equivalence for massive bodies". Physical Review Letters 36 (11): 555–558. doi:10.1103/physrevlett.36.555. Bibcode: 1976PhRvL..36..555S. http://prl.aps.org/pdf/PRL/v36/i11/p555_1. 
  36. ↑ Keiser, George M.; Faller, James E. (1979). "New approach to the Eötvös experiment". Bulletin of the American Physical Society 24: 579. 
  37. ↑ Niebauer, Timothy M.; McHugh, Martin P.; Faller, James E. (1987). "Galilean test for the fifth force". Physical Review Letters 59 (6): 609–612. doi:10.1103/physrevlett.59.609. PMID 10035824. Bibcode: 1987PhRvL..59..609N. https://zenodo.org/record/1233860. 
  38. ↑ Stubbs, Christopher W.; Adelberger, Eric G.; Heckel, Blayne R.; Rogers, Warren F.; Swanson, H. Erik; Watanabe, R.; Gundlach, Jens H.; Raab, Frederick J. (1989). "Limits on Composition-Dependent Interactions Using a Laboratory Source: Is There a "Fifth Force" Coupled to Isospin?". Physical Review Letters 62 (6): 609–612. doi:10.1103/physrevlett.62.609. PMID 10040283. Bibcode: 1989PhRvL..62..609S. 
  39. ↑ Adelberger, Eric G.; Stubbs, Christopher W.; Heckel, Blayne R.; Su, Y.; Swanson, H. Erik; Smith, G. L.; Gundlach, Jens H.; Rogers, Warren F. (1990). "Testing the equivalence principle in the field of the Earth: Particle physics at masses below 1 μeV?". Physical Review D 42 (10): 3267–3292. doi:10.1103/physrevd.42.3267. PMID 10012726. Bibcode: 1990PhRvD..42.3267A. 
  40. ↑ Baeßler, Stefan (2001). "Remarks by Heinrich Hertz (1857–94) on the equivalence principle". Classical and Quantum Gravity 18 (13): 2393. doi:10.1088/0264-9381/18/13/301. Bibcode: 2001CQGra..18.2393B. 
  41. ↑ Baeßler, Stefan; Heckel, Blayne R.; Adelberger, Eric G.; Gundlach, Jens H.; Schmidt, Ulrich; Swanson, H. Erik (1999). "Improved Test of the Equivalence Principle for Gravitational Self-Energy". Physical Review Letters 83 (18): 3585. doi:10.1103/physrevlett.83.3585. Bibcode: 1999PhRvL..83.3585B. 
  42. ↑ Schlamminger, Stephan; Choi, Ki-Young; Wagner, Todd A.; Gundlach, Jens H.; Adelberger, Eric G. (2008). "Test of the Equivalence Principle Using a Rotating Torsion Balance". Physical Review Letters 100 (4): 041101. doi:10.1103/PhysRevLett.100.041101. PMID 18352252. Bibcode: 2008PhRvL.100d1101S. 
  43. ↑ Touboul, Pierre; Métris, Gilles; Rodrigues, Manuel; André, Yves; Baghi, Quentin; Bergé, Joël; Boulanger, Damien; Bremer, Stefanie et al. (2017). "MICROSCOPE Mission: First Results of a Space Test of the Equivalence Principle". Physical Review Letters 119 (23): 231101. doi:10.1103/PhysRevLett.119.231101. PMID 29286705. Bibcode: 2017PhRvL.119w1101T. 
  44. ↑ Touboul, P., Métris, G., Rodrigues, M., Bergé, J., Robert, A., Baghi, Q., André, Y., Bedouet, J., Boulanger, D., Bremer, S. and Carle, P. (2022). "MICROSCOPE Mission: Final Results of the Test of the Equivalence Principle.". Physical Review Letters 129 (12): 121102. doi:10.1103/PhysRevLett.129.121102. PMID 36179190. Bibcode: 2022PhRvL.129l1102T. https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.129.121102. 
  45. ↑ "The Eöt-Wash Group | Laboratory Tests of Gravitational and sub-Gravitational Physics". http://www.npl.washington.edu/eotwash/. 
  46. ↑ Dittus, Hansjörg; Lāmmerzahl, Claus (2005). "Experimental Tests of the Equivalence Principle and Newton's Law in Space". Gravitation and Cosmology: 2nd Mexican Meeting on Mathematical and Experimental Physics, AIP Conference Proceedings. 758. p. 95. doi:10.1063/1.1900510. Bibcode: 2005AIPC..758...95D. http://www.zarm.uni-bremen.de/2forschung/gravi/publications/papers/2005DittusLaemmerzahl.pdf. 
  47. ↑ "S T e P". http://einstein.stanford.edu/STEP/. 
  48. ↑ ""GALILEO GALILEI" GG Small Mission Project". http://eotvos.dm.unipi.it/nobili/. 
  49. ↑ Kimura, M.; Aghion, S.; Amsler, C.; Ariga, A.; Ariga, T.; Belov, A.; Bonomi, G.; Bräunig, P. et al. (2015). "Testing the Weak Equivalence Principle with an antimatter beam at CERN". Journal of Physics: Conference Series 631 (1): 012047. doi:10.1088/1742-6596/631/1/012047. Bibcode: 2015JPhCS.631a2047K. http://stacks.iop.org/1742-6596/631/i=1/a=012047. 
  50. ↑ 50.0 50.1 Overduin, James; Everitt, Francis; Mester, John; Worden, Paul (2009). "The Science Case for STEP". Advances in Space Research 43 (10): 1532–1537. doi:10.1016/j.asr.2009.02.012. Bibcode: 2009AdSpR..43.1532O. 
  51. ↑ Uzan, Jean-Philippe (2003-04-07). "The fundamental constants and their variation: observational and theoretical status" (in en). Reviews of Modern Physics 75 (2): 403–455. doi:10.1103/RevModPhys.75.403. ISSN 0034-6861. Bibcode: 2003RvMP...75..403U. https://link.aps.org/doi/10.1103/RevModPhys.75.403. 
  52. ↑ Webb, John K.; Murphy, Michael T.; Flambaum, Victor V.; Dzuba, Vladimir A.; Barrow, John D.; Churchill, Chris W.; Prochaska, Jason X.; Wolfe, Arthur M. (2001). "Further Evidence for Cosmological Evolution of the Fine Structure Constant". Physical Review Letters 87 (9): 091301. doi:10.1103/PhysRevLett.87.091301. PMID 11531558. Bibcode: 2001PhRvL..87i1301W. 
  53. ↑ Rocha, G; Trotta, R; Martins, C.J.A.P; Melchiorri, A; Avelino, P.P; Viana, P.T.P (Nov 2003). "New constraints on varying α" (in en). New Astronomy Reviews 47 (8–10): 863–869. doi:10.1016/j.newar.2003.07.018. Bibcode: 2003NewAR..47..863R. https://linkinghub.elsevier.com/retrieve/pii/S1387647303001532. 
  54. ↑ "Fundamental Physics of Space – Technical Details". http://funphysics.jpl.nasa.gov/technical/grp/lunar-laser.html. 
  55. ↑ Viswanathan, V; Fienga, A; Minazzoli, O; Bernus, L; Laskar, J; Gastineau, M (May 2018). "The new lunar ephemeris INPOP17a and its application to fundamental physics". Monthly Notices of the Royal Astronomical Society 476 (2): 1877–1888. doi:10.1093/mnras/sty096. Bibcode: 2018MNRAS.476.1877V. 
  56. ↑ Ransom, Scott M. (2014). "A millisecond pulsar in a stellar triple system". Nature 505 (7484): 520–524. doi:10.1038/nature12917. PMID 24390352. Bibcode: 2014Natur.505..520R. http://www.nature.com/nature/journal/vaop/ncurrent/full/nature12917.html#ref7. 
  57. ↑ Anne M. Archibald (4 July 2018). "Universality of free fall from the orbital motion of a pulsar in a stellar triple system". Nature 559 (7712): 73–76. doi:10.1038/s41586-018-0265-1. PMID 29973733. Bibcode: 2018Natur.559...73A. 
  58. ↑ "Even Phenomenally Dense Neutron Stars Fall like a Feather – Einstein Gets It Right Again". Charles Blue, Paul Vosteen (NRAO). 4 July 2018. https://public.nrao.edu/news/neutron-stars-fall/. 
  59. ↑ Voisin, G.; Cognard, I.; Freire, P. C. C.; Wex, N.; Guillemot, L.; Desvignes, G.; Kramer, M.; Theureau, G. (2020-06-01). "An improved test of the strong equivalence principle with the pulsar in a triple star system" (in en). Astronomy & Astrophysics 638: A24. doi:10.1051/0004-6361/202038104. ISSN 0004-6361. Bibcode: 2020A&A...638A..24V. https://www.aanda.org/articles/aa/abs/2020/06/aa38104-20/aa38104-20.html. 

Further reading

  • Dicke, Robert H.; "New Research on Old Gravitation", Science 129, 3349 (1959). Explains the value of research on gravitation and distinguishes between the strong (later renamed "Einstein") and weak equivalence principles.
  • Dicke, Robert H.; "Mach's Principle and Equivalence", in Evidence for gravitational theories: proceedings of course 20 of the International School of Physics "Enrico Fermi", ed. C. Møller (Academic Press, New York, 1962). This article outlines the approach to precisely testing general relativity advocated by Dicke and pursued from 1959 onwards.
  • Misner, Charles W.; Thorne, Kip S.; and Wheeler, John A.; Gravitation, New York: W. H. Freeman and Company, 1973, Chapter 16 discusses the equivalence principle.
  • Ohanian, Hans; and Ruffini, Remo; Gravitation and Spacetime 2nd edition, New York: Norton, 1994, ISBN:0-393-96501-5 Chapter 1 discusses the equivalence principle, but incorrectly, according to modern usage, states that the strong equivalence principle is wrong.
  • Will, Clifford M.; Theory and experiment in gravitational physics, Cambridge, UK: Cambridge University Press, 1993. This is the standard technical reference for tests of general relativity.
  • Will, Clifford M.; Was Einstein Right?: Putting General Relativity to the Test, Basic Books (1993). This is a popular account of tests of general relativity.
  • Friedman, Michael; Foundations of Space-Time Theories, Princeton, New Jersey: Princeton University Press, 1983. Chapter V discusses the equivalence principle.

External links



Retrieved from "https://handwiki.org/wiki/index.php?title=Astronomy:Equivalence_principle&oldid=3340881"