Hypercube
|
|
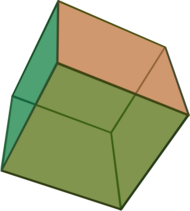
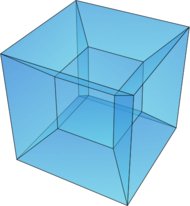
| Cube (3-cube) | Tesseract (4-cube) |
|---|
In geometry, a hypercube is an n-dimensional analogue of a square (n = 2) and a cube (n = 3). It is a closed, compact, convex figure whose 1-skeleton consists of groups of opposite parallel line segments aligned in each of the space's dimensions, perpendicular to each other and of the same length. A unit hypercube's longest diagonal in n dimensions is equal to [math]\displaystyle{ \sqrt{n} }[/math].
An n-dimensional hypercube is more commonly referred to as an n-cube or sometimes as an n-dimensional cube.[citation needed] The term measure polytope (originally from Elte, 1912)[1] is also used, notably in the work of H. S. M. Coxeter who also labels the hypercubes the γn polytopes.[2]
The hypercube is the special case of a hyperrectangle (also called an n-orthotope).
A unit hypercube is a hypercube whose side has length one unit. Often, the hypercube whose corners (or vertices) are the 2n points in Rn with each coordinate equal to 0 or 1 is called the unit hypercube.
Construction
A hypercube can be defined by increasing the numbers of dimensions of a shape:
- 0 – A point is a hypercube of dimension zero.
- 1 – If one moves this point one unit length, it will sweep out a line segment, which is a unit hypercube of dimension one.
- 2 – If one moves this line segment its length in a perpendicular direction from itself; it sweeps out a 2-dimensional square.
- 3 – If one moves the square one unit length in the direction perpendicular to the plane it lies on, it will generate a 3-dimensional cube.
- 4 – If one moves the cube one unit length into the fourth dimension, it generates a 4-dimensional unit hypercube (a unit tesseract).
This can be generalized to any number of dimensions. This process of sweeping out volumes can be formalized mathematically as a Minkowski sum: the d-dimensional hypercube is the Minkowski sum of d mutually perpendicular unit-length line segments, and is therefore an example of a zonotope.
The 1-skeleton of a hypercube is a hypercube graph.
Vertex coordinates
A unit hypercube of dimension [math]\displaystyle{ n }[/math] is the convex hull of all the points whose [math]\displaystyle{ n }[/math] Cartesian coordinates are each equal to either [math]\displaystyle{ 0 }[/math] or [math]\displaystyle{ 1 }[/math]. This hypercube is also the cartesian product [math]\displaystyle{ [0,1]^n }[/math] of [math]\displaystyle{ n }[/math] copies of the unit interval [math]\displaystyle{ [0,1] }[/math]. Another unit hypercube, centered at the origin of the ambient space, can be obtained from this one by a translation. It is the convex hull of the points whose vectors of Cartesian coordinates are
- [math]\displaystyle{ \left(\pm \frac{1}{2}, \pm \frac{1}{2}, \cdots, \pm \frac{1}{2}\right)\!\!. }[/math]
Here the symbol [math]\displaystyle{ \pm }[/math] means that each coordinate is either equal to [math]\displaystyle{ 1/2 }[/math] or to [math]\displaystyle{ -1/2 }[/math]. This unit hypercube is also the cartesian product [math]\displaystyle{ [-1/2,1/2]^n }[/math]. Any unit hypercube has an edge length of [math]\displaystyle{ 1 }[/math] and an [math]\displaystyle{ n }[/math]-dimensional volume of [math]\displaystyle{ 1 }[/math].
The [math]\displaystyle{ n }[/math]-dimensional hypercube obtained as the convex hull of the points with coordinates [math]\displaystyle{ (\pm 1, \pm 1, \cdots, \pm 1) }[/math] or, equivalently as the Cartesian product [math]\displaystyle{ [-1,1]^n }[/math] is also often considered due to the simpler form of its vertex coordinates. Its edge length is [math]\displaystyle{ 2 }[/math], and its [math]\displaystyle{ n }[/math]-dimensional volume is [math]\displaystyle{ 2^n }[/math].
Faces
Every hypercube admits, as its faces, hypercubes of a lower dimension contained in its boundary. A hypercube of dimension [math]\displaystyle{ n }[/math] admits [math]\displaystyle{ 2n }[/math] facets, or faces of dimension [math]\displaystyle{ n-1 }[/math]: a ([math]\displaystyle{ 1 }[/math]-dimensional) line segment has [math]\displaystyle{ 2 }[/math] endpoints; a ([math]\displaystyle{ 2 }[/math]-dimensional) square has [math]\displaystyle{ 4 }[/math] sides or edges; a [math]\displaystyle{ 3 }[/math]-dimensional cube has [math]\displaystyle{ 6 }[/math] square faces; a ([math]\displaystyle{ 4 }[/math]-dimensional) tesseract has [math]\displaystyle{ 8 }[/math] three-dimensional cubes as its facets. The number of vertices of a hypercube of dimension [math]\displaystyle{ n }[/math] is [math]\displaystyle{ 2^n }[/math] (a usual, [math]\displaystyle{ 3 }[/math]-dimensional cube has [math]\displaystyle{ 2^3=8 }[/math] vertices, for instance).
The number of the [math]\displaystyle{ m }[/math]-dimensional hypercubes (just referred to as [math]\displaystyle{ m }[/math]-cubes from here on) contained in the boundary of an [math]\displaystyle{ n }[/math]-cube is
- [math]\displaystyle{ E_{m,n} = 2^{n-m}{n \choose m} }[/math],[3] where [math]\displaystyle{ {n \choose m}=\frac{n!}{m!\,(n-m)!} }[/math] and [math]\displaystyle{ n! }[/math] denotes the factorial of [math]\displaystyle{ n }[/math].
The extended f-vector for an n-cube can be computed by (2,1)n, like the coefficients of polynomial products. For example a tesseract is (2,1)4 = (4,1)2 = (16,32,24,8,1).
For example, the boundary of a [math]\displaystyle{ 4 }[/math]-cube ([math]\displaystyle{ n=4 }[/math]) contains [math]\displaystyle{ 8 }[/math] cubes ([math]\displaystyle{ 3 }[/math]-cubes), [math]\displaystyle{ 24 }[/math] squares ([math]\displaystyle{ 2 }[/math]-cubes), [math]\displaystyle{ 32 }[/math] line segments ([math]\displaystyle{ 1 }[/math]-cubes) and [math]\displaystyle{ 16 }[/math] vertices ([math]\displaystyle{ 0 }[/math]-cubes). This identity can be proven by a simple combinatorial argument: for each of the [math]\displaystyle{ 2^n }[/math] vertices of the hypercube, there are [math]\displaystyle{ \tbinom n m }[/math] ways to choose a collection of [math]\displaystyle{ m }[/math] edges incident to that vertex. Each of these collections defines one of the [math]\displaystyle{ m }[/math]-dimensional faces incident to the considered vertex. Doing this for all the vertices of the hypercube, each of the [math]\displaystyle{ m }[/math]-dimensional faces of the hypercube is counted [math]\displaystyle{ 2^m }[/math] times since it has that many vertices, and we need to divide [math]\displaystyle{ 2^n\tbinom n m }[/math] by this number.
The number of facets of the hypercube can be used to compute the [math]\displaystyle{ (n-1) }[/math]-dimensional volume of its boundary: that volume is [math]\displaystyle{ 2n }[/math] times the volume of a [math]\displaystyle{ (n-1) }[/math]-dimensional hypercube; that is, [math]\displaystyle{ 2ns^{n-1} }[/math] where [math]\displaystyle{ s }[/math] is the length of the edges of the hypercube.
These numbers can also be generated by the linear recurrence relation
- [math]\displaystyle{ E_{m,n} = 2E_{m,n-1} + E_{m-1,n-1} \! }[/math], with [math]\displaystyle{ E_{0,0}= 1 }[/math], and [math]\displaystyle{ E_{m,n}=0 }[/math] when [math]\displaystyle{ n \lt m }[/math], [math]\displaystyle{ n \lt 0 }[/math], or [math]\displaystyle{ m \lt 0 }[/math].
For example, extending a square via its 4 vertices adds one extra line segment (edge) per vertex. Adding the opposite square to form a cube provides [math]\displaystyle{ E_{1,3}=12 }[/math] line segments.
| m | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| n | n-cube | Names | Schläfli Coxeter |
Vertex 0-face |
Edge 1-face |
Face 2-face |
Cell 3-face |
4-face |
5-face |
6-face |
7-face |
8-face |
9-face |
10-face |
| 0 | 0-cube | Point Monon |
( ) Error creating thumbnail: Unable to save thumbnail to destination |
1 | ||||||||||
| 1 | 1-cube | Line segment Dion[4] |
{} Error creating thumbnail: Unable to save thumbnail to destination |
2 | 1 | |||||||||
| 2 | 2-cube | Square Tetragon |
{4} Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination |
4 | 4 | 1 | ||||||||
| 3 | 3-cube | Cube Hexahedron |
{4,3} Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination |
8 | 12 | 6 | 1 | |||||||
| 4 | 4-cube | Tesseract Octachoron |
{4,3,3} Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination |
16 | 32 | 24 | 8 | 1 | ||||||
| 5 | 5-cube | Penteract Deca-5-tope |
{4,3,3,3} Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination |
32 | 80 | 80 | 40 | 10 | 1 | |||||
| 6 | 6-cube | Hexeract Dodeca-6-tope |
{4,3,3,3,3} Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination |
64 | 192 | 240 | 160 | 60 | 12 | 1 | ||||
| 7 | 7-cube | Hepteract Tetradeca-7-tope |
{4,3,3,3,3,3} Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination |
128 | 448 | 672 | 560 | 280 | 84 | 14 | 1 | |||
| 8 | 8-cube | Octeract Hexadeca-8-tope |
{4,3,3,3,3,3,3} Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination |
256 | 1024 | 1792 | 1792 | 1120 | 448 | 112 | 16 | 1 | ||
| 9 | 9-cube | Enneract Octadeca-9-tope |
{4,3,3,3,3,3,3,3} Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination |
512 | 2304 | 4608 | 5376 | 4032 | 2016 | 672 | 144 | 18 | 1 | |
| 10 | 10-cube | Dekeract Icosa-10-tope |
{4,3,3,3,3,3,3,3,3} Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination |
1024 | 5120 | 11520 | 15360 | 13440 | 8064 | 3360 | 960 | 180 | 20 | 1 |
Graphs
An n-cube can be projected inside a regular 2n-gonal polygon by a skew orthogonal projection, shown here from the line segment to the 16-cube.
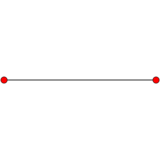 Line segment |
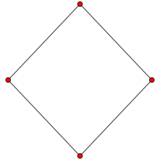 Square |
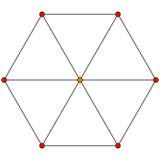 Cube |
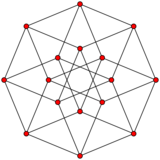 Tesseract |
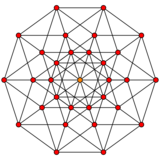 5-cube |
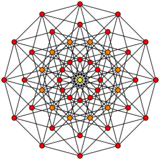 6-cube |
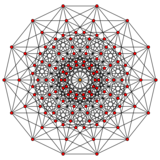 7-cube |
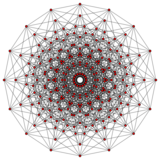 8-cube |
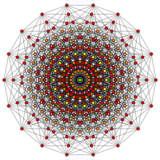 9-cube |
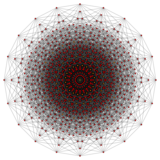 10-cube |
 11-cube |
 12-cube |
 13-cube |
 14-cube |
 15-cube |
 16-cube |
Related families of polytopes
The hypercubes are one of the few families of regular polytopes that are represented in any number of dimensions.
The hypercube (offset) family is one of three regular polytope families, labeled by Coxeter as γn. The other two are the hypercube dual family, the cross-polytopes, labeled as βn, and the simplices, labeled as αn. A fourth family, the infinite tessellations of hypercubes, he labeled as δn.
Another related family of semiregular and uniform polytopes is the demihypercubes, which are constructed from hypercubes with alternate vertices deleted and simplex facets added in the gaps, labeled as hγn.
n-cubes can be combined with their duals (the cross-polytopes) to form compound polytopes:
- In two dimensions, we obtain the octagrammic star figure {8/2},
- In three dimensions we obtain the compound of cube and octahedron,
- In four dimensions we obtain the compound of tesseract and 16-cell.
Relation to (n−1)-simplices
The graph of the n-hypercube's edges is isomorphic to the Hasse diagram of the (n−1)-simplex's face lattice. This can be seen by orienting the n-hypercube so that two opposite vertices lie vertically, corresponding to the (n−1)-simplex itself and the null polytope, respectively. Each vertex connected to the top vertex then uniquely maps to one of the (n−1)-simplex's facets (n−2 faces), and each vertex connected to those vertices maps to one of the simplex's n−3 faces, and so forth, and the vertices connected to the bottom vertex map to the simplex's vertices.
This relation may be used to generate the face lattice of an (n−1)-simplex efficiently, since face lattice enumeration algorithms applicable to general polytopes are more computationally expensive.
Generalized hypercubes
Regular complex polytopes can be defined in complex Hilbert space called generalized hypercubes, γpn = p{4}2{3}...2{3}2, or
..
. Real solutions exist with p = 2, i.e. γ2n = γn = 2{4}2{3}...2{3}2 = {4,3,..,3}. For p > 2, they exist in [math]\displaystyle{ \mathbb{C}^n }[/math]. The facets are generalized (n−1)-cube and the vertex figure are regular simplexes.
The regular polygon perimeter seen in these orthogonal projections is called a petrie polygon. The generalized squares (n = 2) are shown with edges outlined as red and blue alternating color p-edges, while the higher n-cubes are drawn with black outlined p-edges.
The number of m-face elements in a p-generalized n-cube are: [math]\displaystyle{ p^{n-m}{n \choose m} }[/math]. This is pn vertices and pn facets.[5]
| p=2 | p=3 | p=4 | p=5 | p=6 | p=7 | p=8 | ||
|---|---|---|---|---|---|---|---|---|
| [math]\displaystyle{ \mathbb{R}^2 }[/math] |  γ22 = {4} = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 4 vertices |
[math]\displaystyle{ \mathbb{C}^2 }[/math] | 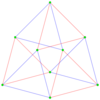 γ32 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 9 vertices |
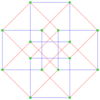 γ42 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 16 vertices |
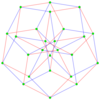 γ52 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 25 vertices |
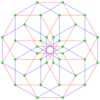 γ62 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 36 vertices |
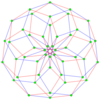 γ72 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 49 vertices |
 γ82 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 64 vertices |
| [math]\displaystyle{ \mathbb{R}^3 }[/math] |  γ23 = {4,3} = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 8 vertices |
[math]\displaystyle{ \mathbb{C}^3 }[/math] | 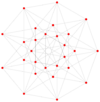 γ33 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 27 vertices |
 γ43 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 64 vertices |
 γ53 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 125 vertices |
 γ63 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 216 vertices |
 γ73 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 343 vertices |
 γ83 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 512 vertices |
| [math]\displaystyle{ \mathbb{R}^4 }[/math] |  γ24 = {4,3,3} = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 16 vertices |
[math]\displaystyle{ \mathbb{C}^4 }[/math] |  γ34 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 81 vertices |
 γ44 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 256 vertices |
 γ54 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 625 vertices |
 γ64 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 1296 vertices |
 γ74 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 2401 vertices |
 γ84 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 4096 vertices |
| [math]\displaystyle{ \mathbb{R}^5 }[/math] |  γ25 = {4,3,3,3} = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 32 vertices |
[math]\displaystyle{ \mathbb{C}^5 }[/math] |  γ35 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 243 vertices |
 γ45 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 1024 vertices |
 γ55 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 3125 vertices |
 γ65 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 7776 vertices |
γ75 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 16,807 vertices |
γ85 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 32,768 vertices |
| [math]\displaystyle{ \mathbb{R}^6 }[/math] |  γ26 = {4,3,3,3,3} = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 64 vertices |
[math]\displaystyle{ \mathbb{C}^6 }[/math] |  γ36 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 729 vertices |
 γ46 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 4096 vertices |
 γ56 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 15,625 vertices |
γ66 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 46,656 vertices |
γ76 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 117,649 vertices |
γ86 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 262,144 vertices |
| [math]\displaystyle{ \mathbb{R}^7 }[/math] |  γ27 = {4,3,3,3,3,3} = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 128 vertices |
[math]\displaystyle{ \mathbb{C}^7 }[/math] |  γ37 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 2187 vertices |
γ47 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 16,384 vertices |
γ57 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 78,125 vertices |
γ67 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 279,936 vertices |
γ77 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 823,543 vertices |
γ87 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 2,097,152 vertices |
| [math]\displaystyle{ \mathbb{R}^8 }[/math] |  γ28 = {4,3,3,3,3,3,3} = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 256 vertices |
[math]\displaystyle{ \mathbb{C}^8 }[/math] |  γ38 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 6561 vertices |
γ48 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 65,536 vertices |
γ58 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 390,625 vertices |
γ68 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 1,679,616 vertices |
γ78 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 5,764,801 vertices |
γ88 = Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination Error creating thumbnail: Unable to save thumbnail to destination 16,777,216 vertices |
Relation to exponentiation
Any positive integer raised to another positive integer power will yield a third integer, with this third integer being a specific type of figurate number corresponding to an n-cube with a number of dimensions corresponding to the exponential. For example, the exponent 2 will yield a square number or "perfect square", which can be arranged into a square shape with a side length corresponding to that of the base. Similarly, the exponent 3 will yield a perfect cube, an integer which can be arranged into a cube shape with a side length of the base. As a result, the act of raising a number to 2 or 3 is more commonly referred to as "squaring" and "cubing", respectively. However, the names of higher-order hypercubes do not appear to be in common use for higher powers.
See also
- Hypercube interconnection network of computer architecture
- Hyperoctahedral group, the symmetry group of the hypercube
- Hypersphere
- Simplex
- Parallelotope
- Crucifixion (Corpus Hypercubus) (famous artwork)
Notes
- ↑ Elte, E. L. (1912). "IV, Five dimensional semiregular polytope". The Semiregular Polytopes of the Hyperspaces. Netherlands: University of Groningen. ISBN 141817968X.
- ↑ Coxeter 1973, pp. 122-123, §7.2 see illustration Fig 7.2C.
- ↑ Coxeter 1973, p. 122, §7·25.
- ↑ Johnson, Norman W.; Geometries and Transformations, Cambridge University Press, 2018, p.224.
- ↑ Coxeter, H. S. M. (1974), Regular complex polytopes, London & New York: Cambridge University Press, p. 180.
References
- Bowen, J. P. (April 1982). "Hypercube". Practical Computing 5 (4): 97–99. http://www.jpbowen.com/publications/ndcubes.html. Retrieved June 30, 2008.
- Coxeter, H. S. M. (1973). Regular Polytopes (3rd ed.). §7.2. see illustration Fig. 7-2C: Dover. pp. 122-123. ISBN 0-486-61480-8. p. 296, Table I (iii): Regular Polytopes, three regular polytopes in n dimensions (n ≥ 5)
- Hill, Frederick J.; Gerald R. Peterson (1974). Introduction to Switching Theory and Logical Design: Second Edition. New York: John Wiley & Sons. ISBN 0-471-39882-9. Cf Chapter 7.1 "Cubical Representation of Boolean Functions" wherein the notion of "hypercube" is introduced as a means of demonstrating a distance-1 code (Gray code) as the vertices of a hypercube, and then the hypercube with its vertices so labelled is squashed into two dimensions to form either a Veitch diagram or Karnaugh map.
External links
- Weisstein, Eric W.. "Hypercube". http://mathworld.wolfram.com/Hypercube.html.
- Weisstein, Eric W.. "Hypercube graphs". http://mathworld.wolfram.com/HypercubeGraph.html.
- Rotating a Hypercube by Enrique Zeleny, Wolfram Demonstrations Project.
- Rudy Rucker and Farideh Dormishian's Hypercube Downloads
- A001787 Number of edges in an n-dimensional hypercube. at OEIS
Fundamental convex regular and uniform polytopes in dimensions 2–10
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 |



