Prismatic uniform 4-polytope

In four-dimensional geometry, a prismatic uniform 4-polytope is a uniform 4-polytope with a nonconnected Coxeter diagram symmetry group.[citation needed] These figures are analogous to the set of prisms and antiprism uniform polyhedra, but add a third category called duoprisms, constructed as a product of two regular polygons.
The prismatic uniform 4-polytopes consist of two infinite families:
- Polyhedral prisms: products of a line segment and a uniform polyhedron. This family is infinite because it includes prisms built on 3-dimensional prisms and antiprisms.
- Duoprisms: product of two regular polygons.
Convex polyhedral prisms
The most obvious family of prismatic 4-polytopes is the polyhedral prisms, i.e. products of a polyhedron with a line segment. The cells of such a 4-polytope are two identical uniform polyhedra lying in parallel hyperplanes (the base cells) and a layer of prisms joining them (the lateral cells). This family includes prisms for the 75 nonprismatic uniform polyhedra (of which 18 are convex; one of these, the cube-prism, is listed above as the tesseract).[citation needed]
There are 18 convex polyhedral prisms created from 5 Platonic solids and 13 Archimedean solids as well as for the infinite families of three-dimensional prisms and antiprisms.[citation needed] The symmetry number of a polyhedral prism is twice that of the base polyhedron.
Tetrahedral prisms: A3 × A1
| # | Johnson Name (Bowers style acronym) | Picture | Coxeter diagram and Schläfli symbols |
Cells by type | Element counts | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| Cells | Faces | Edges | Vertices | |||||||
| 48 | Tetrahedral prism (tepe) | 
|
{3,3}×{} |
2 3.3.3 |
4 3.4.4 |
6 | 8 {3} 6 {4} |
16 | 8 | |
| 49 | Truncated tetrahedral prism (tuttip) | 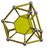
|
t{3,3}×{} |
2 3.6.6 |
4 3.4.4 |
4 4.4.6 |
10 | 8 {3} 18 {4} 8 {6} |
48 | 24 |
| [51] | Rectified tetrahedral prism (Same as octahedral prism) (ope) |

|
r{3,3}×{} |
2 3.3.3.3 |
4 3.4.4 |
6 | 16 {3} 12 {4} |
30 | 12 | |
| [50] | Cantellated tetrahedral prism (Same as cuboctahedral prism) (cope) |

|
rr{3,3}×{} |
2 3.4.3.4 |
8 3.4.4 |
6 4.4.4 |
16 | 16 {3} 36 {4} |
60 | 24 |
| [54] | Cantitruncated tetrahedral prism (Same as truncated octahedral prism) (tope) |
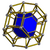
|
tr{3,3}×{} |
2 4.6.6 |
8 3.4.4 |
6 4.4.4 |
16 | 48 {4} 16 {6} |
96 | 48 |
| [59] | Snub tetrahedral prism (Same as icosahedral prism) (ipe) |

|
sr{3,3}×{} |
2 3.3.3.3.3 |
20 3.4.4 |
22 | 40 {3} 30 {4} |
72 | 24 | |
Octahedral prisms: BC3 × A1
| # | Johnson Name (Bowers style acronym) | Picture | Coxeter diagram and Schläfli symbols |
Cells by type | Element counts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cells | Faces | Edges | Vertices | ||||||||
| [10] | Cubic prism (Same as tesseract) (Same as 4-4 duoprism) (tes) |

|
{4,3}×{} |
2 4.4.4 |
6 4.4.4 |
8 | 24 {4} | 32 | 16 | ||
| 50 | Cuboctahedral prism (Same as cantellated tetrahedral prism) (cope) |

|
r{4,3}×{} |
2 3.4.3.4 |
8 3.4.4 |
6 4.4.4 |
16 | 16 {3} 36 {4} |
60 | 24 | |
| 51 | Octahedral prism (Same as rectified tetrahedral prism) (Same as triangular antiprismatic prism) (ope) |

|
{3,4}×{} |
2 3.3.3.3 |
8 3.4.4 |
10 | 16 {3} 12 {4} |
30 | 12 | ||
| 52 | Rhombicuboctahedral prism (sircope) | 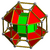
|
rr{4,3}×{} |
2 3.4.4.4 |
8 3.4.4 |
18 4.4.4 |
28 | 16 {3} 84 {4} |
120 | 96 | |
| 53 | Truncated cubic prism (ticcup) | 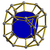
|
t{4,3}×{} |
2 3.8.8 |
8 3.4.4 |
6 4.4.8 |
16 | 16 {3} 36 {4} 12 {8} |
96 | 48 | |
| 54 | Truncated octahedral prism (Same as cantitruncated tetrahedral prism) (tope) |

|
t{3,4}×{} |
2 4.6.6 |
6 4.4.4 |
8 4.4.6 |
16 | 48 {4} 16 {6} |
96 | 48 | |
| 55 | Truncated cuboctahedral prism (gircope) | 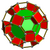
|
tr{4,3}×{} |
2 4.6.8 |
12 4.4.4 |
8 4.4.6 |
6 4.4.8 |
28 | 96 {4} 16 {6} 12 {8} |
192 | 96 |
| 56 | Snub cubic prism (sniccup) | 
|
sr{4,3}×{} |
2 3.3.3.3.4 |
32 3.4.4 |
6 4.4.4 |
40 | 64 {3} 72 {4} |
144 | 48 | |
Icosahedral prisms: H3 × A1
| # | Johnson Name (Bowers style acronym) | Picture | Coxeter diagram and Schläfli symbols |
Cells by type | Element counts | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Cells | Faces | Edges | Vertices | ||||||||
| 57 | Dodecahedral prism (dope) | 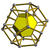
|
{5,3}×{} |
2 5.5.5 |
12 4.4.5 |
14 | 30 {4} 24 {5} |
80 | 40 | ||
| 58 | Icosidodecahedral prism (iddip) | 
|
r{5,3}×{} |
2 3.5.3.5 |
20 3.4.4 |
12 4.4.5 |
34 | 40 {3} 60 {4} 24 {5} |
150 | 60 | |
| 59 | Icosahedral prism (same as snub tetrahedral prism) (ipe) |

|
{3,5}×{} |
2 3.3.3.3.3 |
20 3.4.4 |
22 | 40 {3} 30 {4} |
72 | 24 | ||
| 60 | Truncated dodecahedral prism (tiddip) | 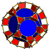
|
t{5,3}×{} |
2 3.10.10 |
20 3.4.4 |
12 4.4.5 |
34 | 40 {3} 90 {4} 24 {10} |
240 | 120 | |
| 61 | Rhombicosidodecahedral prism (sriddip) | 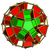
|
rr{5,3}×{} |
2 3.4.5.4 |
20 3.4.4 |
30 4.4.4 |
12 4.4.5 |
64 | 40 {3} 180 {4} 24 {5} |
300 | 120 |
| 62 | Truncated icosahedral prism (tipe) | 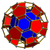
|
t{3,5}×{} |
2 5.6.6 |
12 4.4.5 |
20 4.4.6 |
34 | 90 {4} 24 {5} 40 {6} |
240 | 120 | |
| 63 | Truncated icosidodecahedral prism (griddip) | 
|
tr{5,3}×{} |
2 4.6.4.10 |
30 4.4.4 |
20 4.4.6 |
12 4.4.10 |
64 | 240 {4} 40 {6} 24 {5} |
480 | 240 |
| 64 | Snub dodecahedral prism (sniddip) | 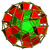
|
sr{5,3}×{} |
2 3.3.3.3.5 |
80 3.4.4 |
12 4.4.5 |
94 | 240 {4} 40 {6} 24 {10} |
360 | 120 | |
Duoprisms: [p] × [q]
 3-3 |
 3-4 |
 3-5 |
 3-6 |
 3-7 |
 3-8 |
 4-3 |
 4-4 |
 4-5 |
 4-6 |
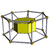 4-7 |
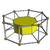 4-8 |
 5-3 |
 5-4 |
 5-5 |
 5-6 |
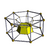 5-7 |
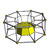 5-8 |
 6-3 |
 6-4 |
 6-5 |
 6-6 |
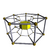 6-7 |
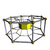 6-8 |
 7-3 |
 7-4 |
 7-5 |
 7-6 |
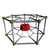 7-7 |
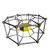 7-8 |
 8-3 |
 8-4 |
 8-5 |
 8-6 |
 8-7 |
 8-8 |
The second is the infinite family of uniform duoprisms, products of two regular polygons.
Their Coxeter diagram is of the form ![]()
![]()
![]()
![]()
![]()
![]()
![]()
This family overlaps with the first: when one of the two "factor" polygons is a square, the product is equivalent to a hyperprism whose base is a three-dimensional prism. The symmetry number of a duoprism whose factors are a p-gon and a q-gon (a "p,q-duoprism") is 4pq if p≠q; if the factors are both p-gons, the symmetry number is 8p2. The tesseract can also be considered a 4,4-duoprism.
The elements of a p,q-duoprism (p ≥ 3, q ≥ 3) are:
- Cells: p q-gonal prisms, q p-gonal prisms
- Faces: pq squares, p q-gons, q p-gons
- Edges: 2pq
- Vertices: pq
There is no uniform analogue in four dimensions to the infinite family of three-dimensional antiprisms with the exception of the great duoantiprism.
Infinite set of p-q duoprism - ![]()
![]()
![]()
![]()
![]()
![]()
![]() - p q-gonal prisms, q p-gonal prisms:
- p q-gonal prisms, q p-gonal prisms:
- 3-3 duoprism -






 - 6 triangular prisms
- 6 triangular prisms - 3-4 duoprism -






 - 3 cubes, 4 triangular prisms
- 3 cubes, 4 triangular prisms - 4-4 duoprism -






 - 8 cubes (same as tesseract)
- 8 cubes (same as tesseract) - 3-5 duoprism -





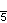
 - 3 pentagonal prisms, 5 triangular prisms
- 3 pentagonal prisms, 5 triangular prisms - 4-5 duoprism -





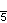
 - 4 pentagonal prisms, 5 cubes
- 4 pentagonal prisms, 5 cubes - 5-5 duoprism -

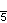



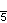
 - 10 pentagonal prisms
- 10 pentagonal prisms - 3-6 duoprism -






 - 3 hexagonal prisms, 6 triangular prisms
- 3 hexagonal prisms, 6 triangular prisms - 4-6 duoprism -






 - 4 hexagonal prisms, 6 cubes
- 4 hexagonal prisms, 6 cubes - 5-6 duoprism -

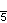




 - 5 hexagonal prisms, 6 pentagonal prisms
- 5 hexagonal prisms, 6 pentagonal prisms - 6-6 duoprism -






 - 12 hexagonal prisms
- 12 hexagonal prisms - ...
Polygonal prismatic prisms
The infinite set of uniform prismatic prisms overlaps with the 4-p duoprisms: (p≥3) - ![]()
![]()
![]()
![]()
![]()
![]()
![]() - p cubes and 4 p-gonal prisms - (All are the same as 4-p duoprism)
- p cubes and 4 p-gonal prisms - (All are the same as 4-p duoprism)
- Triangular prismatic prism -






 - 3 cubes and 4 triangular prisms - (same as 3-4 duoprism)
- 3 cubes and 4 triangular prisms - (same as 3-4 duoprism) - Square prismatic prism -






 - 4 cubes and 4 cubes - (same as 4-4 duoprism and same as tesseract)
- 4 cubes and 4 cubes - (same as 4-4 duoprism and same as tesseract) - Pentagonal prismatic prism -

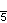




 - 5 cubes and 4 pentagonal prisms - (same as 4-5 duoprism)
- 5 cubes and 4 pentagonal prisms - (same as 4-5 duoprism) - Hexagonal prismatic prism -






 - 6 cubes and 4 hexagonal prisms - (same as 4-6 duoprism)
- 6 cubes and 4 hexagonal prisms - (same as 4-6 duoprism) - Heptagonal prismatic prism -






 - 7 cubes and 4 heptagonal prisms - (same as 4-7 duoprism)
- 7 cubes and 4 heptagonal prisms - (same as 4-7 duoprism) - Octagonal prismatic prism -






 - 8 cubes and 4 octagonal prisms - (same as 4-8 duoprism)
- 8 cubes and 4 octagonal prisms - (same as 4-8 duoprism) - ...
Uniform antiprismatic prism
The infinite sets of uniform antiprismatic prisms or antiduoprisms are constructed from two parallel uniform antiprisms: (p≥3) - ![]()
![]()
![]()
![]()
![]()
![]()
![]() - 2 p-gonal antiprisms, connected by 2 p-gonal prisms and 2p triangular prisms.
- 2 p-gonal antiprisms, connected by 2 p-gonal prisms and 2p triangular prisms.
A p-gonal antiprismatic prism has 4p triangle, 4p square and 4 p-gon faces. It has 10p edges, and 4p vertices.
References
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN:978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation
- Klitzing, Richard. "4D uniform polytopes (polychora)". https://bendwavy.org/klitzing/dimensions/polychora.htm.
Fundamental convex regular and uniform polytopes in dimensions 2–10
| ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||
 |

