Kerr–Newman–de–Sitter metric
The Kerr–Newman–de–Sitter metric (KNdS)[1][2] is the one of the most general stationary solutions of the Einstein–Maxwell equations in general relativity that describes the spacetime geometry in the region surrounding an electrically charged, rotating mass embedded in an expanding universe. It generalizes the Kerr–Newman metric by taking into account the cosmological constant [math]\displaystyle{ \Lambda }[/math].
Boyer–Lindquist coordinates
In (+, −, −, −) signature and in natural units of [math]\displaystyle{ \rm G=M=c=k_e=1 }[/math] the KNdS metric is[3][4][5][6]
[math]\displaystyle{ g_{\rm tt}= \rm -\frac{3 \ [ a^2 \ \sin^2 \theta \left(a^2 \ \Lambda \ \cos^2 \theta +3\right)+a^2 \left(\Lambda \ r^2-3\right)+\Lambda \ r^4-3 \ r^2+6 \ r-3 \mho^2 ] }{\left(a^2 \ \Lambda +3\right)^2 \left(a^2 \cos^2 \theta +r^2\right)} }[/math]
[math]\displaystyle{ g_{\rm rr}= \rm -\frac{a^2 \ \cos^2 \theta +r^2}{\left(a^2+r^2\right) \left(1-\frac{\Lambda \ r^2}{3}\right)-2 \ r+\mho^2} }[/math]
[math]\displaystyle{ g_{\rm \theta \theta}= \rm -\frac{3 \left(a^2 \ \cos^2 \theta +r^2\right)}{a^2 \ \Lambda \ \cos^2 \theta +3} }[/math]
[math]\displaystyle{ g_{\rm \phi \phi}= \rm\frac{9 \ \{ \frac{1}{3} \left(a^2+r^2\right)^2 \sin^2 \theta \left(a^2 \ \Lambda \cos^2 \theta +3\right)-a^2 \sin^4 \theta \ [ \left(a^2+r^2\right) \left(1-\Lambda \ r^2/3\right)-2 \ r+\mho ^2 ] \} }{-\left(a^2 \ \Lambda +3\right)^2 \left(a^2 \cos^2 \theta +r^2\right)} }[/math]
[math]\displaystyle{ g_{\rm t \phi}= \rm \frac{3 \ a \ \sin^2 \theta \ [ a^2 \ \Lambda \left(a^2+r^2\right) \cos^2 \theta +a^2 \ \Lambda \ r^2+\Lambda \ r^4+6 \ r-3 \ \mho^2 ] }{\left(a^2 \ \Lambda +3\right)^2 \left(a^2 \ \cos^2 \theta +r^2\right)} }[/math]
with all the other metric tensor components [math]\displaystyle{ g_{\mu \nu}=0 }[/math], where [math]\displaystyle{ \rm a }[/math] is the black hole's spin parameter, [math]\displaystyle{ \rm \mho }[/math] its electric charge, and [math]\displaystyle{ \rm \Lambda=3 H^2 }[/math][7] the cosmological constant with [math]\displaystyle{ \rm H }[/math] as the time-independent Hubble parameter. The electromagnetic 4-potential is
[math]\displaystyle{ \rm A_{\mu } = \left\{\frac{3 \ r \ \mho }{\left(a^2 \ \Lambda +3\right) \left(a^2 \ \cos^2 \theta +r^2\right)}, \ 0, \ 0, \ -\frac{3 \ a \ r \ \mho \ \sin ^2 \theta }{\left(a^2 \ \Lambda +3\right) \left(a^2 \ \cos^2 \theta +r^2\right)}\right\} }[/math]
The frame-dragging angular velocity is
[math]\displaystyle{ \omega = \frac{\rm d\phi}{\rm d t}= -\frac{g_{\rm t \phi}}{g_{\rm \phi \phi}}= \rm \frac{a \ [ a^2 \ \Lambda \left(a^2+r^2\right) \cos^2 \theta +a^2 \ \Lambda \ r^2+6 \ r+\Lambda \ r^4-3 \ \mho^2 ] }{a^2 \ \sin^2 \theta \ [ a^2 \left(\Lambda \ r^2-3\right)+6 \ r+\Lambda \ r^4-3 \ r^2-3 \ \mho^2 ] +a^2 \ \Lambda \ \left(a^2+r^2\right)^2 \cos^2 \theta +3 \ \left(a^2+r^2\right)^2} }[/math]
and the local frame-dragging velocity relative to constant [math]\displaystyle{ \rm \{r, \theta, \phi \} }[/math] positions (the speed of light at the ergosphere)
[math]\displaystyle{ \nu = \sqrt{g_{\rm t \phi} \ g^{\rm t \phi}} = \rm \sqrt{-\frac{a^2 \ \sin^2 \theta \ [ a^2 \ \Lambda \left(a^2+r^2\right) \cos^2 \theta +a^2 \Lambda \ r^2+6 \ r+\Lambda \ r^4-3 \ \mho^2 ] ^2}{\left(a^2 \ \Lambda \ \cos^2 \theta +3\right) \left(a^2+r^2-a^2 \sin^2 \theta \right)^2 [ a^2 \left(\Lambda \ r^2-3\right)+6 \ r+\Lambda \ r^4-3 \ r^2-3 \ \mho^2 ] }} }[/math]
The escape velocity (the speed of light at the horizons) relative to the local corotating zero-angular momentum observer is
[math]\displaystyle{ {\rm v} = \sqrt{ 1 - 1/g^{\rm tt} } = \rm \sqrt{\frac{3 \left(a^2 \Lambda \cos^2 \theta +3\right) \left(a^2+r^2-a^2 \sin^2 \theta \right)^2 \left[a^2 \left(\Lambda r^2-3\right)+\Lambda r^4-3 r^2+6 r-3 \mho ^2\right]}{\left(a^2 \Lambda +3\right)^2 \left( a^2 \cos^2 \theta +r^2\right) \{ a^2 \Lambda \left( a^2+r^2 \right)^2 \cos^2 \theta +3 \left( a^2+r^2 \right)^2+a^2 \sin^2 \theta \left[a^2 \left(\Lambda r^2-3\right)+\Lambda r^4-3 r^2+6 r-3 \mho ^2 \right] \} }+1} }[/math]
The conserved quantities in the equations of motion
[math]\displaystyle{ {\rm \ddot{x}^{\mu} = -\sum_{\alpha, \beta} \ ( \Gamma^{\mu}_{\alpha \beta} \ \dot{x}^{\alpha} \ \dot{x}^{\beta} + q \ { \rm F}^{\mu \beta} \ {\rm \dot{x}}^{\alpha}} \ g_{\alpha \beta}) }[/math]
where [math]\displaystyle{ \rm \dot{x} }[/math] is the four velocity, [math]\displaystyle{ \rm q }[/math] is the test particle's specific charge and [math]\displaystyle{ \rm F }[/math] the Maxwell–Faraday tensor
[math]\displaystyle{ \rm { \ F}_{\mu \nu}=\frac{\partial A_{\mu}}{\partial x^{\nu}}-\frac{\partial A_{\nu}}{\partial x^{\mu}} }[/math]
are the total energy
[math]\displaystyle{ {\rm E = -p_t}=g_{\rm tt} {\rm \dot{t}}+g_{\rm t \phi} {\rm \dot{\phi}} + \rm q \ A_{t} }[/math]
and the covariant axial angular momentum
[math]\displaystyle{ {\rm L_z = p_{\phi}}=-g_{\rm \phi \phi} {\rm \dot{\phi}}-g_{\rm t \phi} {\rm \dot{t}} - \rm q \ A_{\phi} }[/math]
The overdot stands for differentiation by the testparticle's proper time [math]\displaystyle{ \tau }[/math] or the photon's affine parameter, so [math]\displaystyle{ \rm \dot{x}=dx/d\tau , \ \ddot{x}=d^2x/d\tau^2 }[/math].
Null coordinates
To get [math]\displaystyle{ g_{\rm rr}=0 }[/math] coordinates we apply the transformation
[math]\displaystyle{ \rm dt=du-\frac{dr \left(a^2 \ \Lambda / 3 +1\right) \left(a^2+r^2\right)}{\left(a^2+r^2\right) \left(1-\Lambda \ r^2 / 3 \right)-2 \ r+\mho ^2} }[/math]
[math]\displaystyle{ \rm d \phi = d \varphi-\frac{a \ dr \left(a^2 \ \Lambda / 3 +1\right)}{\left(a^2+r^2\right) \left(1-\Lambda \ r^2 / 3 \right)-2 \ r+ \mho ^2} }[/math]
and get the metric coefficients
[math]\displaystyle{ g_{\rm ur}=\rm -\frac{3}{a^2 \ \Lambda +3} }[/math]
[math]\displaystyle{ g_{\rm r\varphi}=\rm \frac{3 \ a \sin^2 \theta }{a^2 \ \Lambda +3} }[/math]
[math]\displaystyle{ g_{\rm uu}=g_{\rm tt} \ , \ \ g_{\theta \theta}=g_{\theta \theta} \ , \ \ g_{\rm \varphi \varphi}=g_{\rm \phi \phi} \ , \ \ g_{\rm u \varphi}=g_{\rm t \phi} }[/math]
and all the other [math]\displaystyle{ g_{\mu \nu}=0 }[/math], with the electromagnetic vector potential
[math]\displaystyle{ \rm A_{\mu}=\left\{\frac{3 \ r \ \mho }{\left(a^2 \ \Lambda +3\right) \left(a^2 \cos^2 \theta +r^2\right)},\frac{3 \ r \ \mho }{a^2 \left(\Lambda \ r^2-3\right)+6 \ r+\Lambda \ r^4-3 \left(r^2+\mho ^2\right)}, \ 0, \ -\frac{3 \ a \ r \ \mho \sin ^2 \theta }{\left(a^2 \ \Lambda +3\right) \left(a^2 \cos^2 \theta +r^2\right)}\right\} }[/math]
Defining [math]\displaystyle{ \rm \bar{t}=u-r }[/math] ingoing lightlike worldlines give a [math]\displaystyle{ 45^{\circ} }[/math] light cone on a [math]\displaystyle{ \{ \rm \bar{t}, \ r \} }[/math] spacetime diagram.
Horizons and ergospheres
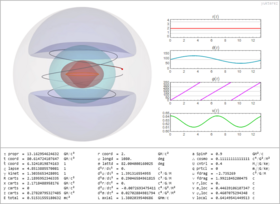
The horizons are at [math]\displaystyle{ g^{\rm rr}=0 }[/math] and the ergospheres at [math]\displaystyle{ g_{\rm tt}||g_{\rm uu}=0 }[/math]. This can be solved numerically or analytically. Like in the Kerr and Kerr–Newman metrics, the horizons have constant Boyer-Lindquist [math]\displaystyle{ \rm r }[/math], while the ergospheres' radii also depend on the polar angle [math]\displaystyle{ \theta }[/math].
This gives 3 positive solutions each (including the black hole's inner and outer horizons and ergospheres as well as the cosmic ones) and a negative solution for the space at [math]\displaystyle{ \rm r\lt 0 }[/math] in the antiverse[8][9] behind the ring singularity, which is part of the probably unphysical extended solution of the metric.
With a negative [math]\displaystyle{ \Lambda }[/math] (the Anti–de–Sitter variant with an attractive cosmological constant), there are no cosmic horizon and ergosphere, only the black hole-related ones.
In the Nariai limit[10] the black hole's outer horizon and ergosphere coincide with the cosmic ones (in the Schwarzschild–de–Sitter metric to which the KNdS reduces with [math]\displaystyle{ \rm a= \mho =0 }[/math] that would be the case when [math]\displaystyle{ \Lambda=1/9 }[/math]).
Invariants
The Ricci scalar for the KNdS metric is [math]\displaystyle{ \rm R=-4 \Lambda }[/math], and the Kretschmann scalar is
[math]\displaystyle{ \rm K=\{220 a^{12} \Lambda ^2 \cos (6 \theta )+66 a^{12} \Lambda ^2 \cos (8 \theta )+12 a^{12} \Lambda ^2 \cos (10 \theta )+a^{12} \Lambda ^2 \cos (12 \theta )+ }[/math]
[math]\displaystyle{ \rm 462 a^{12} \Lambda ^2+1080 a^{10} \Lambda ^2 r^2 \cos (6 \theta )+240 a^{10} \Lambda ^2 r^2 \cos (8 \theta )+24 a^{10} \Lambda ^2 r^2 \cos (10 \theta )+ }[/math]
[math]\displaystyle{ \rm 3024 a^{10} \Lambda ^2 r^2+1920 a^8 \Lambda ^2 r^4 \cos (6 \theta )+ 240 a^8 \Lambda ^2 r^4 \cos (8 \theta )+8400 a^8 \Lambda ^2 r^4- }[/math]
[math]\displaystyle{ \rm 1152 a^6 \cos (6 \theta )-11520 a^6 +1280 a^6 \Lambda ^2 r^6 \cos (6 \theta )+12800 a^6 \Lambda ^2 r^6+207360 a^4 r^2- }[/math]
[math]\displaystyle{ \rm 138240 a^4 r \mho ^2+11520 a^4 \Lambda ^2 r^8+16128 a^4 \mho ^4-276480 a^2 r^4+368640 a^2 r^3 \mho ^2+ }[/math]
[math]\displaystyle{ \rm 6144 a^2 \Lambda ^2 r^{10}-104448 a^2 r^2 \mho ^4+3 a^4 \cos (4 \theta ) [ 165 a^8 \Lambda ^2+960 a^6 \Lambda ^2 r^2+2240 a^4 \Lambda ^2 r^4- }[/math]
[math]\displaystyle{ \rm 256 a^2 (9-10 \Lambda ^2 r^6)+256 (90 r^2-60 r \mho ^2+5 \Lambda ^2 r^8+7 \mho ^4) ] +24 a^2 \cos (2 \theta ) [ 33 a^{10} \Lambda ^2+ }[/math]
[math]\displaystyle{ \rm 210 a^8 \Lambda ^2 r^2+560 a^6 \Lambda ^2 r^4-80 a^4 (9-10 \Lambda ^2 r^6)+128 a^2 (90 r^2-60 r \mho ^2+5 \Lambda ^2 r^8+ }[/math]
[math]\displaystyle{ \rm 7 \mho ^4)+256 r^2 (-45 r^2+60 r \mho ^2+\Lambda ^2 r^8-17 \mho ^4) ] +36864 r^6-73728 r^5 \mho ^2+ }[/math]
[math]\displaystyle{ \rm 2048 \Lambda ^2 r^{12}+43008 r^4 \mho ^4 \} \div \{12 [ a^2 \cos (2 \theta )+a^2+2 r^2 ] ^6 \}\text{.} }[/math]
See also
- Kerr–Newman metric
- De Sitter–Schwarzschild metric
- de Sitter space
- de Sitter universe
- Anti-de Sitter space
- AdS/CFT correspondence
References
- ↑ Stuchlik; Bao; Østgaard; Hledik (2008). "Kerr-Newman-de Sitter black holes with a restricted repulsive barrier of equatorial photon motion". Physical Review D 58: 084003. doi:10.1088/0264-9381/17/21/312.
- ↑ Griffiths; Podolsky (2009). "Exact spacetimes in Einstein's General Relativity". Cambridge University Press, Cambridge Monographs in Mathematical Physics. doi:10.1017/CBO9780511635397. ISBN 9780521889278.
- ↑ Garnier, Arthur (2023). "Motion equations in a Kerr-Newman-de Sitter spacetime". Classical and Quantum Gravity 40 (13). doi:10.1088/1361-6382/accbfe.
- ↑ Kraniotis (2014). "Gravitational lensing and frame-dragging of light in the Kerr–Newman and the Kerr–Newman (anti) de Sitter black hole spacetimes". General Relativity and Gravitation 46 (11): 1818. doi:10.1007/s10714-014-1818-8. Bibcode: 2014GReGr..46.1818K.
- ↑ Bhattacharya (2018). "Kerr-de Sitter spacetime, Penrose process and the generalized area theorem". Physical Review D 97 (8): 084049. doi:10.1103/PhysRevD.97.084049. Bibcode: 2018PhRvD..97h4049B.
- ↑ Stuchlik; Bao; Østgaard (2021). "Null Hypersurfaces in Kerr-Newman-AdS Black Hole and Super-Entropic Black Hole Spacetimes". Classical and Quantum Gravity 38 (4): 045018. doi:10.1088/1361-6382/abd3e0. Bibcode: 2021CQGra..38d5018I.
- ↑ Gaur; Visser (2023). "Black holes embedded in FLRW cosmologies". arXiv:2308.07374 [gr-qc].
- ↑ Andrew Hamilton: Black hole Penrose diagrams (JILA Colorado)
- ↑ Figure 2 in Stuchlik; Kološ; Kovář; Slany (2020). "Influence of Cosmic Repulsion and Magnetic Fields on Accretion Disks Rotating around Kerr Black Holes". Universe 6 (2): 26. doi:10.3390/universe6020026. ISSN 2218-1997. Bibcode: 2020Univ....6...26S.
- ↑ Leonard Susskind: Aspects of de Sitter Holography, timestamp 38:27: video of the online seminar on de Sitter space and Holography, Sept 14, 2021
 |