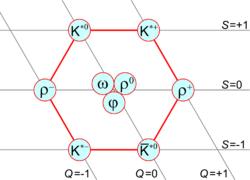
Physics:Vector meson

Short description: Meson with total spin 1 and odd parity

The vector mesons consisting of light quarks form a nonet.

In high energy physics, a vector meson is a meson with total spin 1 and odd parity (usually noted as J^P = 1⁻). Vector mesons have been seen in experiments since the 1960s, and are well known for their spectroscopic pattern of masses.

The vector mesons contrast with the pseudovector mesons, which also have a total spin 1 but instead have even parity. The vector and pseudovector mesons are also dissimilar in that the spectroscopy of vector mesons tends to show nearly pure states of constituent quark flavors, whereas pseudovector mesons and scalar mesons tend to be expressed as composites of mixed states.

Uniquely pure flavor states

Since the development of the quark model by Murray Gell-Mann (and also independently by George Zweig),<ref>{{cite journal |last=Gell-Mann |first=M. |author-link=Murray Gell-Mann |date=4 January 1964

|title=A Schematic Model of Baryons and Mesons |journal=Physics Letters

These nearly pure states characteristic of the vector mesons are not at all evident in the pseudoscalar meson or scalar meson multiplets, and may be only slightly realized among the tensor meson and pseudovector meson multiplets. This fact makes the vector mesons an excellent probe of the quark flavor content of other types of mesons, measured through the respective decay rates of non-vector mesons into the different types of vector mesons. Such experiments are very revealing for theorists who seek to determine the flavor content of mixed state mesons.

Backbone of meson spectroscopy

At higher masses, the vector mesons include charm and bottom quarks in their structure. In this realm, the radiative processes tend to stand out, with heavy tensor and scalar mesons decaying dominantly into vector mesons by photon emission. Pseudovector mesons transition by a similar process into pseudoscalar mesons. Because much of the spectrum of heavy mesons is tied by radiative processes to the vector mesons, one may think of vector mesons as forming a sort of backbone to the spectroscopy of mesons in general.

Some vector mesons can, compared to other mesons, be measured to a very high precision. This stems from the fact that they have the same quantum numbers as the photon, J^PC = 1⁻⁻, where J = angular momentum quantum number, P = parity, C = C parity. Therefore they appear in electron-positron collisions in the process [math]\displaystyle{ e^- e^+ \to \gamma \to q\bar q }[/math], which provides experimentally a clear signal compared to other measurements, which have to use hadronic processes. Vector mesons play a huge role in the study of the strong hadronic force.

List of vector mesons

• ρ meson
• ω meson
• φ meson
• K*(892) meson
• D* meson
• J/ψ meson
• ϒ meson

Hypothetical

• θ meson

See also

• List of mesons
• Vector meson dominance
• Vector boson