Physics:Roton

From HandWiki
Short description: Collective excitation in superfluid helium-4 (a quasiparticle)
Roton dispersion relation, showing the quasiparticle energy E(p) as a function of momentum p. A quasiparticle with momentum generated in the local energy minimum is called a roton.

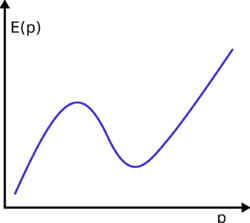
In theoretical physics, a roton is an elementary excitation, or quasiparticle, seen in superfluid helium-4 and Bose–Einstein condensates with long-range dipolar interactions or spin-orbit coupling. The dispersion relation of elementary excitations in this superfluid shows a linear increase from the origin, but exhibits first a maximum and then a minimum in energy as the momentum increases. Excitations with momenta in the linear region are called phonons; those with momenta close to the minimum are called rotons. Excitations with momenta near the maximum are called maxons.

The term "roton-like" is also used for the predicted eigenmodes in 3D metamaterials using beyond-nearest-neighbor coupling.[1][2] The observation of such a "roton-like" dispersion relation was demonstrated under ambient conditions for both acoustic pressure waves in a channel-based metamaterial at audible frequencies and transverse elastic waves in a microscale metamaterial at ultrasound frequencies.[3]

Models

Originally, the roton spectrum was phenomenologically introduced by Lev Landau in 1947.[4] Currently there exist different models which try to explain the roton spectrum with different degrees of success and fundamentality.[5][6] The requirement for any model of this kind is that it must explain not only the shape of the spectrum itself but also other related observables, such as the speed of sound and structure factor of superfluid helium-4. Microwave and Bragg spectroscopy has been conducted on helium to study the roton spectrum.[7]

Bose–Einstein condensation

Bose–Einstein condensation of rotons has been also proposed and studied.[8] Its first detection has been reported in 2018.[9] Under specific conditions the roton minimum gives rise to a crystal solid-like structure called the supersolid, as shown in experiments from 2019.[10][11][12]

See also

References

  1. ↑ Wang, Ke; Chen, Yi; Kadic, Muamer; Wang, Changguo; Wegener, Martin (24 May 2022). "Nonlocal interaction engineering of 2D roton-like dispersion relations in acoustic and mechanical metamaterials". Communications Materials 3 (1): 35. doi:10.1038/s43246-022-00257-z. Bibcode: 2022CoMat...3...35W. 
  2. ↑ Chen, Yi; Kadic, Muamer; Wegener, Martin (2 June 2021). "Roton-like acoustical dispersion relations in 3D metamaterials". Nature Communications 12 (1): 3278. doi:10.1038/s41467-021-23574-2. PMID 34078904. Bibcode: 2021NatCo..12.3278C. 
  3. ↑ Iglesias Martínez, Julio Andrés; Groß, Michael Fidelis; Chen, Yi; Frenzel, Tobias; Laude, Vincent; Kadic, Muamer; Wegener, Martin (2021-12-03). "Experimental observation of roton-like dispersion relations in metamaterials" (in en). Science Advances 7 (49): eabm2189. doi:10.1126/sciadv.abm2189. ISSN 2375-2548. PMID 34851658. Bibcode: 2021SciA....7.2189I. 
  4. ↑ Landau, L. D. (1947). On the theory of superfluidity of helium II. Physics-Uspekhi, 11(1), 91.
  5. ↑ Bisset, R. N.; Blakie, P. B. (26 June 2013). "Fingerprinting Rotons in a Dipolar Condensate: Super-Poissonian Peak in the Atom-Number Fluctuations". Phys. Rev. Lett. 110 (26): 265302. doi:10.1103/PhysRevLett.110.265302. PMID 23848891. Bibcode: 2013PhRvL.110z5302B. 
  6. ↑ Blakie, P. B.; Baillie, D.; Bisset, R. N. (Aug 15, 2012). "Roton spectroscopy in a harmonically trapped dipolar Bose–Einstein condensate". Phys. Rev. A 86 (2): 021604. doi:10.1103/PhysRevA.86.021604. Bibcode: 2012PhRvA..86b1604B. 
  7. ↑ Rybalko, A.; Rubets, S.; Rudavskii, E.; Tikhiy, V.; Poluectov, Y.; Golovashchenko, R.; Derkach, V.; Tarapov, S. et al. (4 Nov 2009). "Microwave Spectroscopy of Condensed Helium at the Roton Frequency". Journal of Low Temperature Physics 158 (1–2): 244–249. doi:10.1007/s10909-009-0025-6. Bibcode: 2010JLTP..158..244R. 
  8. ↑ Glyde, Henry R. (December 1993). "The role of the condensate in the existence of phonons and rotons". Journal of Low Temperature Physics 93 (5–6): 861–878. doi:10.1007/BF00692035. Bibcode: 1993JLTP...93..861G. 
  9. ↑ Chomaz, L. (2018). "Observation of roton mode population in a dipolar quantum gas". Nature Physics 14 (5): 442–446. doi:10.1038/s41567-018-0054-7. PMID 29861780. Bibcode: 2018NatPh..14..442C. 
  10. ↑ Donner, Tobias (3 April 2019). "Dipolar Quantum Gases go Supersolid". Physics 12: 38. doi:10.1103/Physics.12.38. Bibcode: 2019PhyOJ..12...38D. 
  11. ↑ "Three teams independently show dipolar quantum gasses support state of supersolid properties". https://phys.org/news/2019-04-teams-independently-dipolar-quantum-gasses.html. 
  12. ↑ Henkel, N.; Nath, R.; Pohl, T. (11 May 2010). "Three-Dimensional Roton Excitations and Supersolid Formation in Rydberg-Excited Bose-Einstein Condensates". Physical Review Letters 104 (19): 195302. doi:10.1103/PhysRevLett.104.195302. PMID 20866972. Bibcode: 2010PhRvL.104s5302H. 

Bibliography



Retrieved from "https://handwiki.org/wiki/index.php?title=Physics:Roton&oldid=3278670"