Physics:Exotic meson
In particle physics, exotic mesons are mesons that have quantum numbers not possible in the quark model; some proposals for non-standard quark model mesons could be:
- glueballs or gluonium
- Glueballs have no valence quarks at all.
- tetraquarks
- Tetraquarks have two valence quark–antiquark pairs.
- hybrid mesons
- Hybrid mesons contain a valence quark–antiquark pair and one or more gluons.
All exotic mesons are classed as mesons because they are hadrons and carry zero baryon number. Of these, glueballs must be flavor singlets – that is, must have zero isospin, strangeness, charm, bottomness, and topness. Like all particle states, exotic mesons are specified by the quantum numbers which label representations of the Poincaré symmetry, q.e., by the mass (enclosed in parentheses), and by JPC, where J is the angular momentum, P is the intrinsic parity, and C is the charge conjugation parity; One also often specifies the isospin I of the meson. Typically, every quark model meson comes in SU(3) flavor nonet: an octet and an associated flavor singlet. A glueball shows up as an extra (supernumerary) particle outside the nonet.
In spite of such seemingly simple counting, the assignment of any given state as a glueball, tetraquark, or hybrid remains tentative even today, hence the preference for the more generic term exotic meson. Even when there is agreement that one of several states is one of these non-quark model mesons, the degree of mixing, and the precise assignment is fraught with uncertainties. There is also the considerable experimental labor of assigning quantum numbers to each state and crosschecking them in other experiments. As a result, all assignments outside the quark model are tentative. The remainder of this article outlines the situation as it stood at the end of 2004.
Lattice predictions
Lattice QCD predictions for glueballs are now fairly settled, at least when virtual quarks are neglected. The two lowest states are
- 0++ with mass of 1.611±0.163 GeV/c2 and
- 2++ with mass of 2.232±0.310 GeV/c2
The 0−+ and exotic glueballs such as 0−− are all expected to lie above 2 GeV/c2. Glueballs are necessarily isoscalar (both for strong isospin, and trivially, weak isospin), with I = T = 0 .
The ground state hybrid mesons 0−+, 1−+, 1−−, and 2−+ all lie a little below 2 GeV/c2. The hybrid with exotic quantum numbers 1−+ is at 1.9±0.2 GeV/c2. The best lattice computations to date are made in the quenched approximation, which neglects virtual quarks loops. As a result, these computations miss mixing with meson states.
0++ states
The data show five isoscalar resonances: f0(500), f0(980), f0(1370), f0(1500), and f0(1710). Of these the f0(500) is usually identified with the σ of chiral models. The decays and production of f0(1710) give strong evidence that it is also a meson.
Glueball candidate
The f0(1370) and f0(1500) cannot both be a quark model meson, because one is supernumerary. The production of the higher mass state in two photon reactions such as 2γ → 2π or 2γ → 2K reactions is highly suppressed. The decays also give some evidence that one of these could be a glueball.
Tetraquark candidate
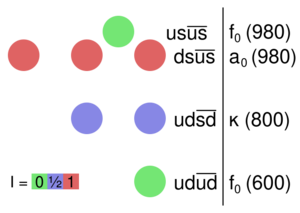
The f0(980) has been identified by some authors as a tetraquark meson, along with the I = 1 states a0(980) and κ0(800). Two long-lived (narrow in the jargon of particle spectroscopy) states: the scalar (0++) state D*±sJ(2317) and the vector (1+) meson D*±sJ(2460), observed at CLEO and BaBar, have also been tentatively identified as tetraquark states. However, for these, other explanations are possible.
2++ states
Two isoscalar states are definitely identified: f2(1270) and the f2′(1525). No other states have been consistently identified by all experiments. Hence it is difficult to say more about these states.
1−+ and other states
The two isovector exotics π1(1400) and π1(1600) seem to be well established experimentally.[1][2][3] A recent coupled-channel analysis has shown these states, which were initially considered separate, are consistent with a single pole. A second exotic state is disfavored.[4] The assignment of these states as hybrids is favored. Lattice QCD calculations show the lightest π1 with 1−+ quantum numbers has strong overlap with operators featuring gluonic construction.[5]
The π(1800) 0−+, ρ(1900) 1−− and the η2(1870) 2−+ are fairly well identified states, which have been tentatively identified as hybrids by some authors. If this identification is correct, then it is a remarkable agreement with lattice computations, which place several hybrids in this range of masses.
See also
- Quark model, mesons, baryons, quarks, and gluons
- Exotic hadrons and exotic baryons
- Quantum chromodynamics, flavor, and the QCD vacuum
- GlueX, an experiment which will explore the spectrum of glueballs and exotic mesons
References
- ↑ Alekseev, M.G.; Alexakhin, V.Yu.; Alexandrov, Yu.; Alexeev, G.D.; Amoroso, A.; Austregesilo, A. et al. (2018). "Observation of a JPC=1−+ exotic resonance in diffractive dissociation of 190 GeV/c2 π− into π−π−π+". Physical Review Letters 104 (24): 092003. doi:10.1103/PhysRevLett.104.241803. PMID 20867295.
- ↑ Aghasyan, M.; Alexeev, M.G.; Alexeev, G.D.; Amoroso, A.; Andrieux, V.; Anfimov, N.V. et al. (2018). "Light isovector resonances in π−p → π−π−π+p at 190 GeV/c2". Physical Review D 98 (9): 241803. doi:10.1103/PhysRevD.98.092003. Bibcode: 2018PhRvD..98i2003A.
- ↑ Adolph, C.; Akhunzyanov, R.; Alexeev, M.G.; Alexeev, G.D.; Amoroso, A.; Andrieux, V. et al. (2015). "Odd and even partial waves of ηπ− and η′π− in π−p → η(′)π−p at 191 GeV/c2". Physics Letters B 740: 303–311. doi:10.1016/j.physletb.2014.11.058.
- ↑ Rodas, A.; Pilloni, A.; Albaladejo, M.; Fernández-Ramírez, C.; Jackura, A.; Mathieu, V. et al. (2019). "Determination of the Pole Position of the Lightest Hybrid Meson Candidate". Physical Review Letters 122 (4): 042002. doi:10.1103/PhysRevLett.122.042002. PMID 30768338. Bibcode: 2019PhRvL.122d2002R.
- ↑ Dudek, Jozef J.; Edwards, Robert G.; Guo, Peng; Thomas, Christopher E. (2013). "Toward the excited isoscalar meson spectrum from lattice QCD". Physical Review D 88 (9): 094505. doi:10.1103/PhysRevD.88.094505. Bibcode: 2013PhRvD..88i4505D.
Further reading
- Yao, W.-M. (2006). "Review of Particle Physics: Non-qq mesons". Journal of Physics G 33 (1): 1. doi:10.1088/0954-3899/33/1/001. Bibcode: 2006JPhG...33....1Y. http://pdg.lbl.gov/2006/reviews/nonqqbar_mxxx050.pdf.
 |

