Physics:Fission barrier

Short description: Activation energy required for a nucleus of an atom to undergo fission

An induced fission reaction. A nucleus becomes excited by some nuclear process and then splits into lighter elements (fission products). This releases a small amount of neutrons and prompt gamma radiation, followed by the beta decay of the lighter nuclei with additional gamma radiation released.

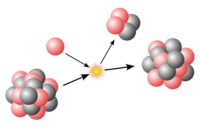
In nuclear physics and nuclear chemistry, the fission barrier is the activation energy required for a nucleus of an atom to undergo fission. This barrier may also be defined as the minimum amount of energy required to deform the nucleus to the point where it is irretrievably committed to the fission process. The energy to overcome this barrier can come from either neutron bombardment of the nucleus, where the additional energy from the neutron brings the nucleus to an excited state and undergoes deformation, or through spontaneous fission, where the nucleus is already in an excited and deformed state.

It is important to note that efforts to understand fission processes are still an ongoing and have been a very difficult problem to solve since fission was first discovered by Lise Meitner, Otto Hahn, and Fritz Strassmann in 1938. While nuclear physicists understand many aspects of the fission process, there is currently no encompassing theoretical framework that gives a satisfactory account of the basic observations.

Scission

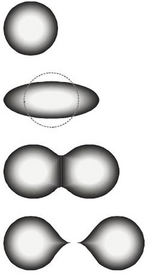
The fission process can be understood when a nucleus with some equilibrium deformation absorbs energy (through neutron capture, for example), becomes excited and deforms to a configuration known as the "transition state" or "saddle point" configuration. As the nucleus deforms, the nuclear Coulomb energy decreases while the nuclear surface energy increases. At the saddle point, the rate of change of the Coulomb energy is equal to the rate of change of the nuclear surface energy. The formation and eventual decay of this transition state nucleus is the rate-determining step in the fission process and corresponds to the passage over an activation energy barrier to the fission reaction. When this occurs, the neck between the nascent fragments disappears and the nucleus divides into two fragments. The point at which this occurs is called the "scission point".

Liquid drop model

From the description of the beginning of the fission process to the "scission point," it is apparent that the change of the shape of the nucleus is associated with a change of energy of some kind. In fact, it is the change of two types of energies: (1) the macroscopic energy related to the nuclear bulk properties as given by the liquid drop model and (2) the quantum mechanical energy associated with filling the shell model orbitals. For the nuclear bulk properties with small distortions, the surface, [math]\displaystyle{ E_s }[/math], and Coulomb, [math]\displaystyle{ E_c }[/math], energies are given by:

[math]\displaystyle{ E_s = E_s^0 \left(1 + \frac{2}{5}\alpha_2^2\right) }[/math]

[math]\displaystyle{ E_c = E_c^0 \left(1 - \frac{1}{5}\alpha_2^2\right) }[/math]

where [math]\displaystyle{ E_s^0 }[/math] and [math]\displaystyle{ E_c^0 }[/math] are the surface and Coulomb energies of the undistorted spherical drops, respectively, and [math]\displaystyle{ \alpha_2 }[/math] is the quadrupole distortion parameter. When the changes in the Coulomb and surface energies ([math]\displaystyle{ \Delta E_c = E_c^0 - E_c }[/math], [math]\displaystyle{ \Delta E_s = E_s^0 - E_s }[/math]) are equal, the nucleus becomes unstable with respect to fission. At that point, the relationship between the undistorted surface and Coulomb energies becomes:

[math]\displaystyle{ x = \frac{E_c^0}{2 E_s^0} }[/math]

where [math]\displaystyle{ x }[/math] is called the fissionability parameter. If [math]\displaystyle{ x \gt 1 }[/math], the liquid drop energy decreases with increasing [math]\displaystyle{ \alpha_2 }[/math], which leads to fission. If [math]\displaystyle{ x \lt 1 }[/math], then the liquid drop energy decreases with decreasing [math]\displaystyle{ \alpha_2 }[/math], which leads to spherical shapes of the nucleus.

The Coulomb and surface energies of a uniformly charged sphere can be approximated by the following expressions:

[math]\displaystyle{ E_c^0 = \frac{3}{5} \frac{Z^2 e^2}{R_0 A^{1/3}} = a_c \frac{Z^2}{A^{1/3}} }[/math]

[math]\displaystyle{ E_s^0 = 4 \pi R_0^2 S A^{2/3} = a_s A^{2/3} }[/math]

where [math]\displaystyle{ Z }[/math] is the atomic number of the nucleus, [math]\displaystyle{ A }[/math] is the mass number of the nucleus, [math]\displaystyle{ e }[/math] is the charge of an electron, [math]\displaystyle{ R_0 }[/math] is the radius of the undistorted spherical nucleus, [math]\displaystyle{ S }[/math] is the surface tension per unit area of the nucleus, [math]\displaystyle{ a_c = 3e^2/5 R_0 }[/math] and [math]\displaystyle{ a_s = 4 \pi R_0^2 S }[/math]. The equation for the fissionability parameter then becomes:

[math]\displaystyle{ x = \left(\frac{a_c}{2 a_s}\right)\left(\frac{Z^2}{A}\right) = \left(\frac{Z^2}{A}\right)/\left(\frac{Z^2}{A}\right)_{critical} }[/math]

where the ratio of the constant [math]\displaystyle{ \left(a_c/2 a_s\right)^{-1} }[/math] is referred to as [math]\displaystyle{ \left(Z^2/A\right)_{critical} }[/math]. The fissionability of a given nucleus can then be categorized relative to [math]\displaystyle{ \left(Z^2/A\right) }[/math]. As an example, plutonium-239 has a [math]\displaystyle{ \left(Z^2/A\right) }[/math] value of 36.97, while less fissionable nuclei like bismuth-209 have a [math]\displaystyle{ \left(Z^2/A\right) }[/math] value of 32.96.

For all stable nuclei, [math]\displaystyle{ x }[/math] must be less than 1. In that case, the total deformation energy of nuclei undergoing fission will increase by an amount [math]\displaystyle{ (1/5) \alpha_2^2 (2 E_s^0 - E_c^0) }[/math], as the nucleus deforms towards fission. This increase in potential energy can be thought of as the activation energy barrier for the fission reaction. However, modern calculations of the potential energy of deformation for the liquid drop model involve many deformation coordinates aside from [math]\displaystyle{ \alpha_2 }[/math] and represent major computational tasks.

Shell corrections

In order to get more reasonable values for the nuclear masses in the liquid drop model, it is necessary to include shell effects. Soviet physicist Vilen Strutinsky proposed such a method using "shell correction" and corrections for nuclear pairing to the liquid drop model. In this method, the total energy of the nucleus is taken as the sum of the liquid drop model energy, [math]\displaystyle{ E_{LDM} }[/math], the shell, [math]\displaystyle{ \delta S }[/math], and pairing, [math]\displaystyle{ \delta P }[/math], corrections to this energy as:

[math]\displaystyle{ E = E_{LDM} + \sum_{p,n}(\delta S + \delta P) }[/math]

The shell corrections, just like the liquid drop energy, are functions of the nuclear deformation. The shell corrections tend to lower the ground state masses of spherical nuclei with magic or near-magic numbers of neutrons and protons. They also tend to lower the ground state mass of mid shell nuclei at some finite deformation thus accounting for the deformed nature of the actinides. Without these shell effects, the heaviest nuclei could not be observed, as they would decay by spontaneous fission on a time scale much shorter than we can observe.

This combination of macroscopic liquid drop and microscopic shell effects predicts that for nuclei in the U-Pu region, a double-humped fission barrier with equal barrier heights and a deep secondary minimum will occur. For heavier nuclei, like californium, the first barrier is predicted to be much larger than the second barrier and passage over the first barrier is rate determining. In general, there is ample experimental and theoretical evidence that the lowest energy path in the fission process corresponds to having the nucleus, initially in an axially symmetric and mass (reflection) symmetric shape pass over the first maximum in the fission barrier with an axially asymmetric but mass symmetric shape and then to pass over the second maximum in the barrier with an axially symmetric but mass (reflection) asymmetric shape. Because of the complicated multidimensional character of the fission process, there are no simple formulas for the fission barrier heights. However, there are extensive tabulations of experimental characterizations of the fission barrier heights for various nuclei.

See also

• Cold fission
• Nuclear fusion