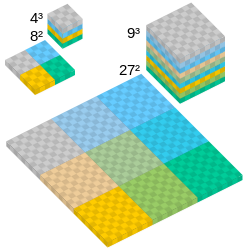
Sixth power

64 (2⁶) and 729 (3⁶) cubelets arranged as cubes (2²³ and 3²³, respectively) and as squares (2³² and 3³², respectively)

In arithmetic and algebra the sixth power of a number n is the result of multiplying six instances of n together. So:

n⁶ = n × n × n × n × n × n.

Sixth powers can be formed by multiplying a number by its fifth power, multiplying the square of a number by its fourth power, by cubing a square, or by squaring a cube.

The sequence of sixth powers of integers is:

0, 1, 64, 729, 4096, 15625, 46656, 117649, 262144, 531441, 1000000, 1771561, 2985984, 4826809, 7529536, 11390625, 16777216, 24137569, 34012224, 47045881, 64000000, 85766121, 113379904, 148035889, 191102976, 244140625, 308915776, 387420489, 481890304, ... (sequence A001014 in the OEIS)

They include the significant decimal numbers 10⁶ (a million), 100⁶ (a short-scale trillion and long-scale billion), 1000⁶ (a Quintillion and a long-scale trillion) and so on.

Squares and cubes

The sixth powers of integers can be characterized as the numbers that are simultaneously squares and cubes. In this way, they are analogous to two other classes of figurate numbers: the square triangular numbers, which are simultaneously square and triangular, and the solutions to the cannonball problem, which are simultaneously square and square-pyramidal.

Because of their connection to squares and cubes, sixth powers play an important role in the study of the Mordell curves, which are elliptic curves of the form

[math]\displaystyle{ y^2=x^3+k. }[/math]

When [math]\displaystyle{ k }[/math] is divisible by a sixth power, this equation can be reduced by dividing by that power to give a simpler equation of the same form. A well-known result in number theory, proven by Rudolf Fueter and Louis J. Mordell, states that, when [math]\displaystyle{ k }[/math] is an integer that is not divisible by a sixth power (other than the exceptional cases [math]\displaystyle{ k=1 }[/math] and [math]\displaystyle{ k=-432 }[/math]), this equation either has no rational solutions with both [math]\displaystyle{ x }[/math] and [math]\displaystyle{ y }[/math] nonzero or infinitely many of them.

In the archaic notation of Robert Recorde, the sixth power of a number was called the "zenzicube", meaning the square of a cube. Similarly, the notation for sixth powers used in 12th century Indian mathematics by Bhāskara II also called them either the square of a cube or the cube of a square.

Sums

There are numerous known examples of sixth powers that can be expressed as the sum of seven other sixth powers, but no examples are yet known of a sixth power expressible as the sum of just six sixth powers. This makes it unique among the powers with exponent k = 1, 2, ... , 8, the others of which can each be expressed as the sum of k other k-th powers, and some of which (in violation of Euler's sum of powers conjecture) can be expressed as a sum of even fewer k-th powers.

In connection with Waring's problem, every sufficiently large integer can be represented as a sum of at most 24 sixth powers of integers.

There are infinitely many different nontrivial solutions to the Diophantine equation

[math]\displaystyle{ a^6+b^6+c^6=d^6+e^6+f^6. }[/math]

It has not been proven whether the equation

[math]\displaystyle{ a^6+b^6=c^6+d^6 }[/math]

has a nontrivial solution, but the Lander, Parkin, and Selfridge conjecture would imply that it does not.

Other properties

• [math]\displaystyle{ n^6-1 }[/math] is divisible by 7 iff n isn't divisible by 7.

See also

• Sextic equation
• Eighth power
• Seventh power
• Fifth power (algebra)
• Fourth power
• Cube (algebra)
• Square (algebra)

External links

• Weisstein, Eric W.. "Diophantine Equation—6th Powers". http://mathworld.wolfram.com/DiophantineEquation6thPowers.html.