Nonhypotenuse number

5 is not a nonhypotenuse number

In mathematics, a nonhypotenuse number is a natural number whose square cannot be written as the sum of two nonzero squares. The name stems from the fact that an edge of length equal to a nonhypotenuse number cannot form the hypotenuse of a right angle triangle with integer sides.

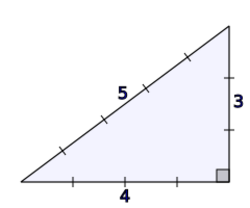
The numbers 1, 2, 3 and 4 are all nonhypotenuse numbers. The number 5, however, is not a nonhypotenuse number as 5² equals 3² + 4².

The first fifty nonhypotenuse numbers are:

1, 2, 3, 4, 6, 7, 8, 9, 11, 12, 14, 16, 18, 19, 21, 22, 23, 24, 27, 28, 31, 32, 33, 36, 38, 42, 43, 44, 46, 47, 48, 49, 54, 56, 57, 59, 62, 63, 64, 66, 67, 69, 71, 72, 76, 77, 79, 81, 83, 84 (sequence A004144 in the OEIS)

Although nonhypotenuse numbers are common among small integers, they become more-and-more sparse for larger numbers. Yet, there are infinitely many nonhypotenuse numbers, and the number of nonhypotenuse numbers not exceeding a value x scales asymptotically with x/√log x.

The nonhypotenuse numbers are those numbers that have no prime factors of the form 4k+1. Equivalently, they are the number that cannot be expressed in the form [math]\displaystyle{ K(m^2+n^2) }[/math] where K, m, and n are all positive integers. A number whose prime factors are not all of the form 4k+1 cannot be the hypotenuse of a primitive integer right triangle (one for which the sides do not have a nontrivial common divisor), but may still be the hypotenuse of a non-primitive triangle.

The nonhypotenuse numbers have been applied to prove the existence of addition chains that compute the first [math]\displaystyle{ n }[/math] square numbers using only [math]\displaystyle{ n+o(n) }[/math] additions.

See also

• Pythagorean theorem
• Landau-Ramanujan constant
• Fermat's theorem on sums of two squares

External links

• OEIS sequence A004144 (Nonhypotenuse numbers)
• OEIS sequence A125667 (Eta numbers)