Squared triangular number

Short description: Square of a triangular number

A square whose side length is a triangular number can be partitioned into squares and half-squares whose areas add to cubes. From (Gulley 2010). The nth coloured region shows n squares of dimension n by n (the rectangle is 1 evenly divided square), hence the area of the nth region is n times n x n.

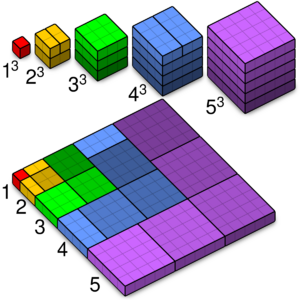
In number theory, the sum of the first n cubes is the square of the nth triangular number. That is,

[math]\displaystyle{ 1^3+2^3+3^3+\cdots+n^3 = \left(1+2+3+\cdots+n\right)^2. }[/math]

The same equation may be written more compactly using the mathematical notation for summation:

[math]\displaystyle{ \sum_{k=1}^n k^3 = \left(\sum_{k=1}^n k\right)^2. }[/math]

This identity is sometimes called Nicomachus's theorem, after Nicomachus of Gerasa (c. 60 – c. 120 CE).

History

Nicomachus, at the end of Chapter 20 of his Introduction to Arithmetic, pointed out that if one writes a list of the odd numbers, the first is the cube of 1, the sum of the next two is the cube of 2, the sum of the next three is the cube of 3, and so on. He does not go further than this, but from this it follows that the sum of the first n cubes equals the sum of the first n(n + 1)/2 odd numbers, that is, the odd numbers from 1 to n(n + 1) − 1. The average of these numbers is obviously n(n + 1)/2, and there are n(n + 1)/2 of them, so their sum is (n(n + 1)/2)².

Many early mathematicians have studied and provided proofs of Nicomachus's theorem. (Stroeker 1995) claims that "every student of number theory surely must have marveled at this miraculous fact". (Pengelley 2002) finds references to the identity not only in the works of Nicomachus in what is now Jordan in the 1st century CE, but also in those of Aryabhata in India in the 5th century, and in those of Al-Karaji c. 1000 in Persia. (Bressoud 2004) mentions several additional early mathematical works on this formula, by Al-Qabisi (10th century Arabia), Gersonides (c. 1300, France), and Nilakantha Somayaji (c. 1500, India); he reproduces Nilakantha's visual proof.

Numeric values; geometric and probabilistic interpretation

All 36 (= (1 + 2 + 3)² = 1³ + 2³ + 3³) rectangles, including 14 (= 1² + 2² + 3²) squares (red), in a 3 × 3 square (4 × 4 vertex) grid

The sequence of squared triangular numbers is

0, 1, 9, 36, 100, 225, 441, 784, 1296, 2025, 3025, 4356, 6084, 8281, ... .

These numbers can be viewed as figurate numbers, a four-dimensional hyperpyramidal generalization of the triangular numbers and square pyramidal numbers.

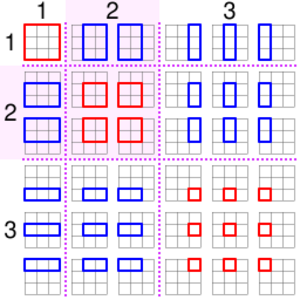
As (Stein 1971) observes, these numbers also count the number of rectangles with horizontal and vertical sides formed in an n × n grid. For instance, the points of a 4 × 4 grid (or a square made up of three smaller squares on a side) can form 36 different rectangles. The number of squares in a square grid is similarly counted by the square pyramidal numbers.

The identity also admits a natural probabilistic interpretation as follows. Let X, Y, Z, W be four integer numbers independently and uniformly chosen at random between 1 and n. Then, the probability that W is the largest of the four numbers equals the probability that Y is at least as large as X and that W is at least as large as Z. That is, P[max(X, Y, Z) ≤ W] = P[X ≤ Y ∧ Z ≤ W]. For any particular value of W, the combinations of X, Y, and Z that make W largest form a cube 1 ≤ X, Y, Z ≤ n so (adding the size of this cube over all choices of W) the number of combinations of X, Y, Z, W for which W is largest is a sum of cubes, the left hand side of the Nichomachus identity. The sets of pairs (X, Y) with X ≤ Y and of pairs (Z, W) with Z ≤ W form isosceles right triangles, and the set counted by the right hand side of the equation of probabilities is the Cartesian product of these two triangles, so its size is the square of a triangular number on the right hand side of the Nichomachus identity. The probabilities themselves are respectively the left and right sides of the Nichomachus identity, normalized to make probabilities by dividing both sides by n⁴.

Proofs

Charles Wheatstone (1854) gives a particularly simple derivation, by expanding each cube in the sum into a set of consecutive odd numbers. He begins by giving the identity [math]\displaystyle{ n^3 = \underbrace{\left(n^2-n+1\right) + \left(n^2-n+1+2\right) + \left(n^2-n+1+4\right)+ \cdots + \left(n^2+n-1\right)}_{n \text{ consecutive odd numbers}}. }[/math] That identity is related to triangular numbers T_n in the following way: [math]\displaystyle{ n^3 =\sum _{k=T_{n-1}+1}^{T_{n}} (2 k-1), }[/math] and thus the summands forming n³ start off just after those forming all previous values 1³ up to (n − 1)³. Applying this property, along with another well-known identity: [math]\displaystyle{ n^2 = \sum_{k=1}^n (2k-1), }[/math] produces the following derivation: [math]\displaystyle{ \begin{align} \sum_{k=1}^n k^3 &= 1 + 8 + 27 + 64 + \cdots + n^3 \\ &= \underbrace{1}_{1^3} + \underbrace{3+5}_{2^3} + \underbrace{7 + 9 + 11}_{3^3} + \underbrace{13 + 15 + 17 + 19}_{4^3} + \cdots + \underbrace{\left(n^2-n+1\right) + \cdots + \left(n^2+n-1\right)}_{n^3} \\ &= \underbrace{\underbrace{\underbrace{\underbrace{1}_{1^2} + 3}_{2^2} + 5}_{3^2} + \cdots + \left(n^2 + n - 1\right)}_{\left( \frac{n^{2}+n}{2} \right)^{2}} \\ &= (1 + 2 + \cdots + n)^2 \\ &= \left(\sum_{k=1}^n k\right)^2. \end{align} }[/math]

(Row 1893) obtains another proof by summing the numbers in a square multiplication table in two different ways. The sum of the ith row is i times a triangular number, from which it follows that the sum of all the rows is the square of a triangular number. Alternatively, one can decompose the table into a sequence of nested gnomons, each consisting of the products in which the larger of the two terms is some fixed value. The sum within each gmonon is a cube, so the sum of the whole table is a sum of cubes.

Visual demonstration that the square of a triangular number equals a sum of cubes.

In the more recent mathematical literature, (Edmonds 1957) provides a proof using summation by parts. (Stein 1971) uses the rectangle-counting interpretation of these numbers to form a geometric proof of the identity (see also Benjamin, Quinn & Wurtz 2006); he observes that it may also be proved easily (but uninformatively) by induction, and states that (Toeplitz 1963) provides "an interesting old Arabic proof". (Kanim 2004) provides a purely visual proof, (Benjamin Orrison) provide two additional proofs, and (Nelsen 1993) gives seven geometric proofs.

Generalizations

A similar result to Nicomachus's theorem holds for all power sums, namely that odd power sums (sums of odd powers) are a polynomial in triangular numbers. These are called Faulhaber polynomials, of which the sum of cubes is the simplest and most elegant example. However, in no other case is one power sum a square of another.

(Stroeker 1995) studies more general conditions under which the sum of a consecutive sequence of cubes forms a square. (Garrett Hummel) and (Warnaar 2004) study polynomial analogues of the square triangular number formula, in which series of polynomials add to the square of another polynomial.

References

• "Two quick combinatorial proofs of [math]\displaystyle{ \textstyle \sum k^3 = {n+1\choose 2}^2 }[/math]", College Mathematics Journal 33 (5): 406–408, 2002, doi:10.2307/1559017, http://www.math.hmc.edu/~orrison/research/papers/two_quick.pdf .
• "Summing cubes by counting rectangles", College Mathematics Journal 37 (5): 387–389, 2006, doi:10.2307/27646391, http://www.math.hmc.edu/~benjamin/papers/rectangles.pdf .
• Bressoud, David (2004), Calculus before Newton and Leibniz, Part III, AP Central, http://www.macalester.edu/~bressoud/pub/CBN3.pdf .
• "Sums of powers of the natural numbers", The Mathematical Gazette 41 (337): 187–188, 1957, doi:10.2307/3609189 
• Garrett, Kristina C.; Hummel, Kristen (2004), "A combinatorial proof of the sum of q-cubes", Electronic Journal of Combinatorics 11 (1): Research Paper 9, doi:10.37236/1762, http://www.combinatorics.org/Volume_11/Abstracts/v11i1r9.html .
• Gulley, Ned (March 4, 2010), Shure, Loren, ed., Nicomachus's Theorem, Matlab Central, http://blogs.mathworks.com/loren/2010/03/04/nichomachuss-theorem/ .
• Kanim, Katherine (2004), "Proofs without words: The sum of cubes—An extension of Archimedes' sum of squares", Mathematics Magazine 77 (4): 298–299, doi:10.2307/3219288 .
• Nelsen, Roger B. (1993), Proofs without Words, Cambridge University Press, ISBN 978-0-88385-700-7 .
• Pengelley, David (2002), "The bridge between continuous and discrete via original sources", Study the Masters: The Abel-Fauvel Conference, National Center for Mathematics Education, Univ. of Gothenburg, Sweden, http://www.math.nmsu.edu/~davidp/bridge.pdf .
• Row, T. Sundara (1893), Geometric Exercises in Paper Folding, Madras: Addison, pp. 47–48 .
• Stein, Robert G. (1971), "A combinatorial proof that [math]\displaystyle{ \textstyle \sum k^3 = (\sum k)^2 }[/math]", Mathematics Magazine 44 (3): 161–162, doi:10.2307/2688231 .
• Stroeker, R. J. (1995), "On the sum of consecutive cubes being a perfect square", Compositio Mathematica 97 (1–2): 295–307, http://www.numdam.org/item?id=CM_1995__97_1-2_295_0 .
• Toeplitz, Otto (1963), The Calculus, a Genetic Approach, University of Chicago Press, ISBN 978-0-226-80667-9 .
• Warnaar, S. Ole (2004), "On the q-analogue of the sum of cubes", Electronic Journal of Combinatorics 11 (1): Note 13, doi:10.37236/1854, http://www.combinatorics.org/Volume_11/Abstracts/v11i1n13.html .
• Wheatstone, C. (1854), "On the formation of powers from arithmetical progressions", Proceedings of the Royal Society of London 7: 145–151, doi:10.1098/rspl.1854.0036, Bibcode: 1854RSPS....7..145W, https://zenodo.org/record/1432033 .

External links

• Weisstein, Eric W.. "Nicomachus's theorem". http://mathworld.wolfram.com/NicomachussTheorem.html. 
• A visual proof of Nicomachus's theorem