Astronomy:Radiation zone

Short description: Radiative layer of stars

An illustration of the structure of the Sun

• Granules
• Sunspot
• Photosphere
• Chromosphere
• Convection zone
• Radiation zone
• Tachocline
• Solar core
• Solar corona
• Flare
• Prominence
• Solar wind

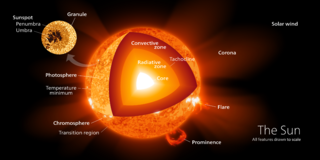
A radiation zone, or radiative region is a layer of a star's interior where energy is primarily transported toward the exterior by means of radiative diffusion and thermal conduction, rather than by convection. Energy travels through the radiation zone in the form of electromagnetic radiation as photons.

Matter in a radiation zone is so dense that photons can travel only a short distance before they are absorbed or scattered by another particle, gradually shifting to longer wavelength as they do so. For this reason, it takes an average of 171,000 years for gamma rays from the core of the Sun to leave the radiation zone. Over this range, the temperature of the plasma drops from 15 million K near the core down to 1.5 million K at the base of the convection zone.

Temperature gradient

In a radiative zone, the temperature gradient—the change in temperature (T) as a function of radius (r)—is given by:

[math]\displaystyle{ \frac{\text{d}T(r)}{\text{d}r}\ =\ -\frac{3 \kappa(r) \rho(r) L(r)}{(4 \pi r^2)(16 \sigma_B) T^3(r)} }[/math]

where κ(r) is the opacity, ρ(r) is the matter density, L(r) is the luminosity, and σ_B is the Stefan–Boltzmann constant. Hence the opacity (κ) and radiation flux (L) within a given layer of a star are important factors in determining how effective radiative diffusion is at transporting energy. A high opacity or high luminosity can cause a high temperature gradient, which results from a slow flow of energy. Those layers where convection is more effective than radiative diffusion at transporting energy, thereby creating a lower temperature gradient, will become convection zones.

This relation can be derived by integrating Fick's first law over the surface of some radius r, giving the total outgoing energy flux which is equal to the luminosity by conservation of energy:

[math]\displaystyle{ L = -4\pi\,r^2 D\frac{\partial u}{\partial r} }[/math]

Where D is the photons diffusion coefficient, and u is the energy density.

The energy density is related to the temperature by Stefan–Boltzmann law by:

[math]\displaystyle{ U = \frac{4}{c} \, \sigma_B \, T^4 }[/math]

Finally, as in the elementary theory of diffusion coefficient in gases, the diffusion coefficient D approximately satisfies:

[math]\displaystyle{ D = \frac{1}{3}c\,\lambda }[/math]

where λ is the photon mean free path, and is the reciprocal of the opacity κ.

Eddington stellar model

Eddington assumed the pressure P in a star is a combination of an ideal gas pressure and radiation pressure, and that there is a constant ratio, β, of the gas pressure to the total pressure. Therefore, by the ideal gas law:

[math]\displaystyle{ \beta P = k_B\frac{\rho}{\mu}T }[/math]

where k_B is Boltzmann constant and μ the mass of a single atom (actually, an ion since matter is ionized; usually a hydrogen ion, i.e. a proton). While the radiation pressure satisfies:

[math]\displaystyle{ 1-\beta = \frac{P_\text{radiation}}{P} =\frac{u}{3P} =\frac{4\sigma_B}{3c} \frac{T^4}{P} }[/math]

so that T⁴ is proportional to P throughout the star.

This gives the polytropic equation (with n=3):

[math]\displaystyle{ P = \left(\frac{3c k_B^4}{4\sigma_B\mu^4}\frac{1-\beta}{\beta^4}\right)^{1/3}\rho^{4/3} }[/math]

Using the hydrostatic equilibrium equation, the second equation becomes equivalent to:

[math]\displaystyle{ -\frac{GM\rho}{r^2} = \frac{\text{d}P}{\text{d}r} = \frac{16\sigma_B}{3c(1-\beta)}T^3\frac{\text{d}T}{\text{d}r} }[/math]

For energy transmission by radiation only, we may use the equation for the temperature gradient (presented in the previous subsection) for the right-hand side and get

[math]\displaystyle{ GM = \frac{\kappa L}{4\pi c (1-\beta)} }[/math]

Thus the Eddington model is a good approximation in the radiation zone as long as κL/M is approximately constant, which is often the case.

Stability against convection

The radiation zone is stable against formation of convection cells if the density gradient is high enough, so that an element moving upwards has its density lowered (due to adiabatic expansion) less than the drop in density of its surrounding, so that it will experience a net buoyancy force downwards.

The criterion for this is:

[math]\displaystyle{ \frac{\text{d}\,\log\,\rho}{\text{d}\,\log\, P} \gt \frac{1}{\gamma_{ad}} }[/math]

where P is the pressure, ρ the density and [math]\displaystyle{ \gamma_{ad} }[/math] is the heat capacity ratio.

For a homogenic ideal gas, this is equivalent to:

[math]\displaystyle{ \frac{\text{d}\,\log\,T}{\text{d}\,\log\, P} \lt 1-\frac{1}{\gamma_{ad}} }[/math]

We can calculate the left-hand side by dividing the equation for the temperature gradient by the equation relating the pressure gradient to the gravity acceleration g:

[math]\displaystyle{ \frac{\text{d}P(r)}{\text{d}r}\ =\ g\rho \ = \ \frac{G\,M(r)\,\rho(r)}{r^2} }[/math]

M(r) being the mass within the sphere of radius r, and is approximately the whole star mass for large enough r.

This gives the following form of the Schwarzschild criterion for stability against convection:

[math]\displaystyle{ \frac{3}{64\pi\sigma_B\,G} \frac{\kappa\,L}{M}\frac{P}{T^4} \lt 1-\frac{1}{\gamma_{ad}} }[/math]

Note that for non-homogenic gas this criterion should be replaced by the Ledoux criterion, because the density gradient now also depends on concentration gradients.

For a polytrope solution with n=3 (as in the Eddington stellar model for radiation zone), P is proportional to T⁴ and the left-hand side is constant and equals 1/4, smaller than the ideal monatomic gas approximation for the right-hand side giving [math]\displaystyle{ 1-1/\gamma_{ad}=2/5 }[/math]. This explains the stability of the radiation zone against convection.

However, at a large enough radius, the opacity κ increases due to the decrease in temperature (by Kramers' opacity law), and possibly also due to a smaller degree of ionization in the lower shells of heavy elements ions. This leads to a violation of the stability criterion and to the creation of the convection zone; in the sun, opacity increases by more than a tenfold across the radiation zone, before the transition to the convection zone happens.

Additional situations in which this stability criterion is not met are:

• Large values of [math]\displaystyle{ L(r)/M(r) }[/math], which may happen towards the star core's center, where M(r) is small, if nuclear energy production is strongly peaked at the center, as in relatively massive stars. Thus such stars have a convective core.
• A smaller value of [math]\displaystyle{ \gamma_{ad} }[/math]. For semi-ionized gas, where approximately half of the atoms are ionized, the effective value of [math]\displaystyle{ \gamma_{ad} }[/math] drops to 6/5, giving [math]\displaystyle{ 1-1/\gamma_{ad}=1/6 }[/math]. Therefore, all stars have shallow convection zones near their surfaces, at low enough temperatures where ionization is only partial.

Main sequence stars

For main sequence stars—those stars that are generating energy through the thermonuclear fusion of hydrogen at the core, the presence and location of radiative regions depends on the star's mass. Main sequence stars below about 0.3 solar masses are entirely convective, meaning they do not have a radiative zone. From 0.3 to 1.2 solar masses, the region around the stellar core is a radiation zone, separated from the overlying convection zone by the tachocline. The radius of the radiative zone increases monotonically with mass, with stars around 1.2 solar masses being almost entirely radiative. Above 1.2 solar masses, the core region becomes a convection zone and the overlying region is a radiation zone, with the amount of mass within the convective zone increasing with the mass of the star.

The Sun

In the Sun, the region between the solar core at 0.2 of the Sun's radius and the outer convection zone at 0.71 of the Sun's radius is referred to as the radiation zone, although the core is also a radiative region. The convection zone and the radiation zone are divided by the tachocline, another part of the Sun.

External links

• SOHO ... Solar and Heliospheric Observatory — official site of this NASA and ESA joint project.
• Animated explanation of the Radiation zone (University of South Wales).
• Animated explanation of the temperature and density of the Radiation zone (University of South Wales).