Astronomy:Stellar parallax

Short description: Concept in astronomy

Stellar parallax is the basis for the parsec, which is the distance from the Sun to an astronomical object that has a parallax angle of one arcsecond. (1 AU and 1 parsec are not to scale, 1 parsec = ~206265 AU)

Stellar parallax is the apparent shift of position (parallax) of any nearby star (or other object) against the background of distant stars. By extension, it is a method for determining the distance to the star through trigonometry, the stellar parallax method. Created by the different orbital positions of Earth, the extremely small observed shift is largest at time intervals of about six months, when Earth arrives at opposite sides of the Sun in its orbit, giving a baseline distance of about two astronomical units between observations. The parallax itself is considered to be half of this maximum, about equivalent to the observational shift that would occur due to the different positions of Earth and the Sun, a baseline of one astronomical unit (AU).

Stellar parallax is so difficult to detect that its existence was the subject of much debate in astronomy for hundreds of years. Thomas Henderson, Friedrich Georg Wilhelm von Struve, and Friedrich Bessel made first successful parallax measurements in 1832–1838, for the stars Alpha Centauri, Vega, and 61 Cygni.

Parallax method

Principle

Throughout the year the position of a star S is noted in relation to other stars in its apparent neighborhood:

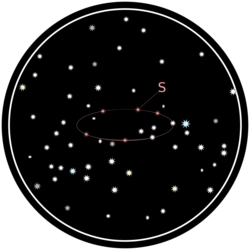
Stars that did not seem to move in relation to each other are used as reference points to determine the path of S.

The observed path is an ellipse: the projection of Earth’s orbit around the Sun through S onto the distant background of non-moving stars. The farther S is removed from Earth’s orbital axis, the greater the eccentricity of the path of S. The center of the ellipse corresponds to the point where S would be seen from the Sun:

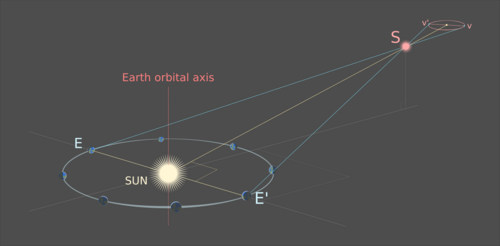
The plane of Earth’s orbit is at an angle to a line from the Sun through S. The vertices v and v' of the elliptical projection of the path of S are projections of positions of Earth E and E’ such that a line E-E’ intersects the line Sun-S at a right angle; the triangle created by points E, E’ and S is an isosceles triangle with the line Sun-S as its symmetry axis.

Any stars that did not move between observations are, for the purpose of the accuracy of the measurement, infinitely far away. This means that the distance of the movement of the Earth compared to the distance to these infinitely far away stars is, within the accuracy of the measurement, 0. Thus a line of sight from Earth's first position E to vertex v will be essentially the same as a line of sight from the Earth's second position E' to the same vertex v, and will therefore run parallel to it - impossible to depict convincingly in an image of limited size:

Since line E'-v' is a transversal in the same (approximately Euclidean) plane as parallel lines E-v and E'-v, it follows that the corresponding angles of intersection of these parallel lines with this transversal are congruent: the angle θ between lines of sight E-v and E'-v' is equal to the angle θ between E'-v and E'-v', which is the angle θ between observed positions of S in relation to its apparently unmoving stellar surroundings.

The distance d from the Sun to S now follows from simple trigonometry:

       tan(½θ) = E-Sun / d,

so that d = E-Sun / tan(½θ), where E-Sun is 1 AU.

The more distant an object is, the smaller its parallax.

Stellar parallax measures are given in the tiny units of arcseconds, or even in thousandths of arcseconds (milliarcseconds). The distance unit parsec is defined as the length of the leg of a right triangle adjacent to the angle of one arcsecond at one vertex, where the other leg is 1 AU long. Because stellar parallaxes and distances all involve such skinny right triangles, a convenient trigonometric approximation can be used to convert parallaxes (in arcseconds) to distance (in parsecs). The approximate distance is simply the reciprocal of the parallax: [math]\displaystyle{ d \text{ (pc)} \approx 1 / p \text{ (arcsec)}. }[/math] For example, Proxima Centauri (the nearest star to Earth other than the Sun), whose parallax is 0.7685, is 1 / 0.7685 parsecs = 1.301 parsecs (4.24 ly) distant.

Variants

Stellar parallax is most often measured using annual parallax, defined as the difference in position of a star as seen from Earth and Sun, i.e. the angle subtended at a star by the mean radius of Earth's orbit around the Sun. The parsec (3.26 light-years) is defined as the distance for which the annual parallax is 1 arcsecond. Annual parallax is normally measured by observing the position of a star at different times of the year as Earth moves through its orbit.

The angles involved in these calculations are very small and thus difficult to measure. The nearest star to the Sun (and also the star with the largest parallax), Proxima Centauri, has a parallax of 0.7685 ± 0.0002 arcsec. This angle is approximately that subtended by an object 2 centimeters in diameter located 5.3 kilometers away.

Derivation

For a right triangle,

[math]\displaystyle{ \tan p = \frac {1\,\text{au}} {d} , }[/math]

where [math]\displaystyle{ p }[/math] is the parallax, 1 au (149,600,000 km) is approximately the average distance from the Sun to Earth, and [math]\displaystyle{ d }[/math] is the distance to the star. Using small-angle approximations (valid when the angle is small compared to 1 radian),

[math]\displaystyle{ \tan x \approx x\text{ radians} = x \cdot \frac {180} {\pi} \text{ degrees} = x \cdot 180 \cdot \frac {3600} {\pi} \text{ arcseconds} , }[/math]

so the parallax, measured in arcseconds, is

[math]\displaystyle{ p'' \approx \frac {1 \text{ au}} {d} \cdot 180 \cdot \frac{3600} {\pi} . }[/math]

If the parallax is 1", then the distance is

[math]\displaystyle{ d = 1 \text{ au} \cdot 180 \cdot \frac {3600} {\pi} \approx 206,265 \text{ au} \approx 3.2616 \text{ ly} \equiv 1 \text{ parsec} . }[/math]

This defines the parsec, a convenient unit for measuring distance using parallax. Therefore, the distance, measured in parsecs, is simply [math]\displaystyle{ d = 1 / p }[/math], when the parallax is given in arcseconds.

Error

Precise parallax measurements of distance have an associated error. This error in the measured parallax angle does not translate directly into an error for the distance, except for relatively small errors. The reason for this is that an error toward a smaller angle results in a greater error in distance than an error toward a larger angle.

However, an approximation of the distance error can be computed by

[math]\displaystyle{ \delta d = \delta \left( {1 \over p} \right) =\left| {\partial \over \partial p} \left( {1 \over p} \right) \right| \delta p ={\delta p \over p^2} }[/math]

where d is the distance and p is the parallax. The approximation is far more accurate for parallax errors that are small relative to the parallax than for relatively large errors. For meaningful results in stellar astronomy, Dutch astronomer Floor van Leeuwen recommends that the parallax error be no more than 10% of the total parallax when computing this error estimate.

History of measurement

Early theory and attempts

The Dollond heliometer of the late 1700s

Stellar parallax is so small that it was unobservable until the 19th century, and its apparent absence was used as a scientific argument against heliocentrism during the early modern age. It is clear from Euclid's geometry that the effect would be undetectable if the stars were far enough away, but for various reasons, such gigantic distances involved seemed entirely implausible: it was one of Tycho Brahe's principal objections to Copernican heliocentrism that for it to be compatible with the lack of observable stellar parallax, there would have to be an enormous and unlikely void between the orbit of Saturn and the eighth sphere (the fixed stars).

James Bradley first tried to measure stellar parallaxes in 1729. The stellar movement proved too insignificant for his telescope, but he instead discovered the aberration of light and the nutation of Earth's axis, and catalogued 3,222 stars.

19th and 20th centuries

Bessel's heliometer

The split lens of the Bamberg Heliometer (late 19th century)

Measurement of annual parallax was the first reliable way to determine the distances to the closest stars. In the second quarter of the 19^th century, technological progress reached to the level which provided sufficient accuracy and precision for stellar parallax measurements. Giuseppe Calandrelli noted stellar parallax in 1805-6 and came up with a 4-second value for the star Vega which was a gross overestimate. The first successful stellar parallax measurements were done by Thomas Henderson in Cape Town South Africa in 1832–1833, where he measured parallax of one of the closest stars, Alpha Centauri. Between 1835 and 1836, astronomer Friedrich Georg Wilhelm von Struve at the Dorpat university observatory measured the distance of Vega, publishing his results in 1837. Friedrich Bessel, a friend of Struve, carried out an intense observational campaign in 1837–1838 at Koenigsberg Observatory for the star 61 Cygni using a heliometer, and published his results in 1838. Henderson published his results in 1839, after returning from South Africa.

Those three results, two of which were measured with the best instruments at the time (Fraunhofer great refractor used by Struve and Fraunhofer heliometer by Bessel) were the first ones in history to establish the reliable distance scale to the stars.

A large heliometer was installed at Kuffner Observatory (In Vienna) in 1896, and was used for measuring the distance to other stars by trigonometric parallax. By 1910 it had computed 16 parallax distances to other stars, out of only 108 total known to science at that time.

Diagram of a heliometer from the 1911 Encyclopædia Britannica, which would be a view looking towards the split lens of a heliometer

Being very difficult to measure, only about 60 stellar parallaxes had been obtained by the end of the 19th century, mostly by use of the filar micrometer. Astrographs using astronomical photographic plates sped the process in the early 20th century. Automated plate-measuring machines and more sophisticated computer technology of the 1960s allowed more efficient compilation of star catalogues. In the 1980s, charge-coupled devices (CCDs) replaced photographic plates and reduced optical uncertainties to one milliarcsecond.

Stellar parallax remains the standard for calibrating other measurement methods (see Cosmic distance ladder). Accurate calculations of distance based on stellar parallax require a measurement of the distance from Earth to the Sun, now known to exquisite accuracy based on radar reflection off the surfaces of planets.

Space astrometry

Hubble precision stellar distance measurement has been extended 10 times further into the Milky Way.

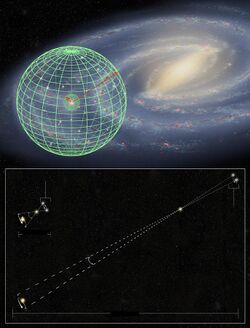
In 1989, the satellite Hipparcos was launched primarily for obtaining parallaxes and proper motions of nearby stars, increasing the number of stellar parallaxes measured to milliarcsecond accuracy a thousandfold. Even so, Hipparcos is only able to measure parallax angles for stars up to about 1,600 light-years away, a little more than one percent of the diameter of the Milky Way Galaxy.

The Hubble telescope WFC3 now has a precision of 20 to 40 microarcseconds, enabling reliable distance measurements up to 3,066 parsecs (10,000 ly) for a small number of stars. This gives more accuracy to the cosmic distance ladder and improves the knowledge of distances in the Universe, based on the dimensions of the Earth's orbit.

As distances between the two points of observation are increased, the visual effect of the parallax is likewise rendered more visible. NASA's New Horizons spacecraft performed the first interstellar parallax measurement on 22 April 2020, taking images of Proxima Centauri and Wolf 359 in conjunction with earth-based observatories. The relative proximity of the two stars combined with the 6.5 billion kilometer (about 43 AU) distance of the spacecraft from Earth yielded a discernible parallax of arcminutes, allowing the parallax to be seen visually without instrumentation.

Parallax of Proxima Centauri as observed from New Horizons and Earth.

The European Space Agency's Gaia mission, launched 19 December 2013, is expected to measure parallax angles to an accuracy of 10 microarcseconds for all moderately bright stars, thus mapping nearby stars (and potentially planets) up to a distance of tens of thousands of light-years from Earth. Data Release 2 in 2018 claims mean errors for the parallaxes of 15th magnitude and brighter stars of 20–40 microarcseconds.

Radio astrometry

Very long baseline interferometry in the radio band can produce images with angular resolutions of about 1 milliarcsecond, and hence, for bright radio sources, the precision of parallax measurements made in the radio can easily exceed those of optical telescopes like Gaia. These measurements tend to be sensitivity limited, and need to be made one at a time, so the work is generally done only for sources like pulsars and X-ray binaries, where the radio emission is strong relative to the optical emission.

See also

• Apparent place
• TAU (spacecraft) (an abandoned space mission project that would have used parallax)

References

• Hirshfeld, Alan w. (2001). Parallax: The Race to Measure the Cosmos. New York: W. H. Freeman. ISBN 0-7167-3711-6. https://archive.org/details/parallax00alan. 
• Whipple, Fred L. (2007). Earth Moon and Planets. Read Books. ISBN 978-1-4067-6413-0. .
• Zeilik, Michael A.; Gregory, Stephan A. (1998). Introductory Astronomy & Astrophysics (4th ed.). Saunders College Publishing. ISBN 0-03-006228-4. .

Further reading

• Dyson, F. W. (1915). "Measurement of the distances of the stars". The Observatory 38: 292. Bibcode: 1915Obs....38..292D.