Schröder number
| Named after | Ernst Schröder |
|---|---|
| No. of known terms | infinity |
| First terms | 1, 2, 6, 22, 90, 394, 1806 |
| OEIS index |
|
In mathematics, the Schröder number [math]\displaystyle{ S_n, }[/math] also called a large Schröder number or big Schröder number, describes the number of lattice paths from the southwest corner [math]\displaystyle{ (0,0) }[/math] of an [math]\displaystyle{ n \times n }[/math] grid to the northeast corner [math]\displaystyle{ (n,n), }[/math] using only single steps north, [math]\displaystyle{ (0,1); }[/math] northeast, [math]\displaystyle{ (1,1); }[/math] or east, [math]\displaystyle{ (1,0), }[/math] that do not rise above the SW–NE diagonal.[1]
The first few Schröder numbers are
where [math]\displaystyle{ S_0=1 }[/math] and [math]\displaystyle{ S_1=2. }[/math] They were named after the German mathematician Ernst Schröder.
Examples
The following figure shows the 6 such paths through a [math]\displaystyle{ 2 \times 2 }[/math] grid:
Related constructions
A Schröder path of length [math]\displaystyle{ n }[/math] is a lattice path from [math]\displaystyle{ (0,0) }[/math] to [math]\displaystyle{ (2n,0) }[/math] with steps northeast, [math]\displaystyle{ (1,1); }[/math] east, [math]\displaystyle{ (2,0); }[/math] and southeast, [math]\displaystyle{ (1,-1), }[/math] that do not go below the [math]\displaystyle{ x }[/math]-axis. The [math]\displaystyle{ n }[/math]th Schröder number is the number of Schröder paths of length [math]\displaystyle{ n }[/math].[2] The following figure shows the 6 Schröder paths of length 2.
Similarly, the Schröder numbers count the number of ways to divide a rectangle into [math]\displaystyle{ n+1 }[/math] smaller rectangles using [math]\displaystyle{ n }[/math] cuts through [math]\displaystyle{ n }[/math] points given inside the rectangle in general position, each cut intersecting one of the points and dividing only a single rectangle in two (i.e., the number of structurally-different guillotine partitions). This is similar to the process of triangulation, in which a shape is divided into nonoverlapping triangles instead of rectangles. The following figure shows the 6 such dissections of a rectangle into 3 rectangles using two cuts:
Pictured below are the 22 dissections of a rectangle into 4 rectangles using three cuts:
The Schröder number [math]\displaystyle{ S_n }[/math] also counts the separable permutations of length [math]\displaystyle{ n-1. }[/math]
Related sequences
Schröder numbers are sometimes called large or big Schröder numbers because there is another Schröder sequence: the little Schröder numbers, also known as the Schröder-Hipparchus numbers or the super-Catalan numbers. The connections between these paths can be seen in a few ways:
- Consider the paths from [math]\displaystyle{ (0,0) }[/math] to [math]\displaystyle{ (n,n) }[/math] with steps [math]\displaystyle{ (1,1), }[/math] [math]\displaystyle{ (2,0), }[/math] and [math]\displaystyle{ (1,-1) }[/math] that do not rise above the main diagonal. There are two types of paths: those that have movements along the main diagonal and those that do not. The (large) Schröder numbers count both types of paths, and the little Schröder numbers count only the paths that only touch the diagonal but have no movements along it.[3]
- Just as there are (large) Schröder paths, a little Schröder path is a Schröder path that has no horizontal steps on the [math]\displaystyle{ x }[/math]-axis.[4]
- If [math]\displaystyle{ S_n }[/math] is the [math]\displaystyle{ n }[/math]th Schröder number and [math]\displaystyle{ s_n }[/math] is the [math]\displaystyle{ n }[/math]th little Schröder number, then [math]\displaystyle{ S_n = 2s_n }[/math] for [math]\displaystyle{ n\gt 0 }[/math] [math]\displaystyle{ (S_0 = s_0 = 1). }[/math][4]
Schröder paths are similar to Dyck paths but allow the horizontal step instead of just diagonal steps. Another similar path is the type of path that the Motzkin numbers count; the Motzkin paths allow the same diagonal paths but allow only a single horizontal step, (1,0), and count such paths from [math]\displaystyle{ (0,0) }[/math] to [math]\displaystyle{ (n,0) }[/math].[5]
There is also a triangular array associated with the Schröder numbers that provides a recurrence relation[6] (though not just with the Schröder numbers). The first few terms are
It is easier to see the connection with the Schröder numbers when the sequence is in its triangular form:
k n
|
0 | 1 | 2 | 3 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|
| 0 | 1 | ||||||
| 1 | 1 | 2 | |||||
| 2 | 1 | 4 | 6 | ||||
| 3 | 1 | 6 | 16 | 22 | |||
| 4 | 1 | 8 | 30 | 68 | 90 | ||
| 5 | 1 | 10 | 48 | 146 | 304 | 394 | |
| 6 | 1 | 12 | 70 | 264 | 714 | 1412 | 1806 |
Then the Schröder numbers are the diagonal entries, i.e. [math]\displaystyle{ S_n = T(n,n) }[/math] where [math]\displaystyle{ T(n,k) }[/math] is the entry in row [math]\displaystyle{ n }[/math] and column [math]\displaystyle{ k }[/math]. The recurrence relation given by this arrangement is
- [math]\displaystyle{ T(n,k) = T(n,k-1) + T(n-1,k-1) + T(n-1,k) }[/math]
with [math]\displaystyle{ T(1,k)=1 }[/math] and [math]\displaystyle{ T(n,k)=0 }[/math] for [math]\displaystyle{ k\gt n }[/math].[6] Another interesting observation to make is that the sum of the [math]\displaystyle{ n }[/math]th row is the [math]\displaystyle{ (n+1) }[/math]st little Schröder number; that is,
- [math]\displaystyle{ \sum_{k=0}^n T(n,k) = s_{n+1} }[/math].
Recurrence relations
With [math]\displaystyle{ S_0 = 1 }[/math], [math]\displaystyle{ S_1 = 2 }[/math], [7]
- [math]\displaystyle{ S_{n} = 3S_{n-1} + \sum_{k=1}^{n-2}S_{k} S_{n-k-1} }[/math] for [math]\displaystyle{ n \geq 2 }[/math]
and also
- [math]\displaystyle{ S_{n} =\frac{6n-3}{n+1}S_{n-1} - \frac{n-2}{n+1}S_{n-2} }[/math] for [math]\displaystyle{ n \geq 2 }[/math]
Generating function
The generating function [math]\displaystyle{ G(x) }[/math] of [math]\displaystyle{ (S_n) }[/math] is
- [math]\displaystyle{ G(x) = \frac{1 - x - \sqrt{x^2 - 6x + 1}}{2x} = \sum_{n=0}^\infty S_n x^n }[/math].[7]
Uses
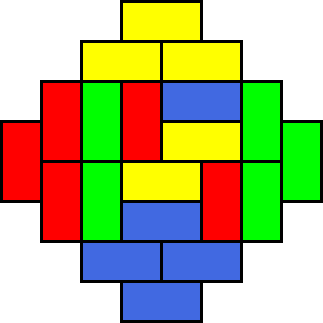
One topic of combinatorics is tiling shapes, and one particular instance of this is domino tilings; the question in this instance is, "How many dominoes (that is, [math]\displaystyle{ 1 \times 2 }[/math] or [math]\displaystyle{ 2 \times 1 }[/math] rectangles) can we arrange on some shape such that none of the dominoes overlap, the entire shape is covered, and none of the dominoes stick out of the shape?" The shape that the Schröder numbers have a connection with is the Aztec diamond. Shown below for reference is an Aztec diamond of order 4 with a possible domino tiling.
It turns out that the determinant of the [math]\displaystyle{ (2n-1)\times(2n-1) }[/math] Hankel matrix of the Schröder numbers, that is, the square matrix whose [math]\displaystyle{ (i,j) }[/math]th entry is [math]\displaystyle{ S_{i+j-1}, }[/math] is the number of domino tilings of the order [math]\displaystyle{ n }[/math] Aztec diamond, which is [math]\displaystyle{ 2^{n(n+1)/2}. }[/math][8] That is,
- [math]\displaystyle{ \begin{vmatrix} S_1 & S_2 & \cdots & S_n \\ S_2 & S_3 & \cdots & S_{n+1} \\ \vdots & \vdots & \ddots & \vdots \\ S_n & S_{n+1} & \cdots & S_{2n-1} \end{vmatrix} = 2^{n(n+1)/2}. }[/math]
For example:
- [math]\displaystyle{ \begin{vmatrix} 2 \end{vmatrix} = 2 = 2^{1(2)/2} }[/math]
- [math]\displaystyle{ \begin{vmatrix} 2 & 6 \\ 6 & 22 \end{vmatrix} = 8 = 2^{2(3)/2} }[/math]
- [math]\displaystyle{ \begin{vmatrix} 2 & 6 & 22 \\ 6 & 22 & 90 \\ 22 & 90 & 394 \end{vmatrix} = 64 = 2^{3(4)/2} }[/math]
See also
- Delannoy number
- Motzkin number
- Narayana number
- Narayana polynomials
- Schröder–Hipparchus number
- Catalan number
References
- ↑ Sloane, N. J. A., ed. "Sequence A006318 (Large Schröder numbers (or large Schroeder numbers, or big Schroeder numbers).)". OEIS Foundation. https://oeis.org/A006318. Retrieved 5 March 2018.
- ↑ Ardila, Federico (2015). "Algebraic and geometric methods in enumerative combinatorics". Handbook of enumerative combinatorics. Boca Raton, FL: CRC Press. pp. 3–172.
- ↑ Sloane, N. J. A., ed. "Sequence A001003 (Schroeder's second problem (generalized parentheses); also called super-Catalan numbers or little Schroeder numbers)". OEIS Foundation. https://oeis.org/A001003. Retrieved 5 March 2018.
- ↑ 4.0 4.1 Drake, Dan (2010). "Bijections from weighted Dyck paths to Schröder paths". arXiv:1006.1959 [math.CO].
- ↑ Deng, Eva Y. P.; Yan, Wei-Jun (2008). "Some identities on the Catalan, Motzkin, and Schröder numbers". Discrete Applied Mathematics 156 (166–218X): 2781–2789. doi:10.1016/j.dam.2007.11.014.
- ↑ 6.0 6.1 Sloane, N. J. A.. "Triangular array associated with Schroeder numbers". https://oeis.org/A033877.
- ↑ 7.0 7.1 Oi, Feng; Guo, Bai-Ni (2017). "Some explicit and recursive formulas of the large and little Schröder numbers". Arab Journal of Mathematical Sciences 23 (1319–5166): 141–147. doi:10.1016/j.ajmsc.2016.06.002.
- ↑ Eu, Sen-Peng; Fu, Tung-Shan (2005). "A simple proof of the Aztec diamond theorem". Electronic Journal of Combinatorics 12 (1077–8926): Research Paper 18, 8. doi:10.37236/1915. http://www.combinatorics.org/Volume_12/Abstracts/v12i1r18.html.
Further reading
- Weisstein, Eric W.. "Schröder Number". http://mathworld.wolfram.com/SchroederNumber.html.
- Stanley, Richard P.: Catalan addendum to Enumerative Combinatorics, Volume 2
 |