Truncated order-4 octagonal tiling

In geometry, the truncated order-4 octagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t_0,1{8,4}. A secondary construction t_0,1,2{8,8} is called a truncated octaoctagonal tiling with two colors of hexakaidecagons.

Constructions

There are two uniform constructions of this tiling, first by the [8,4] kaleidoscope, and second by removing the last mirror, [8,4,1⁺], gives [8,8], (*882).

Two uniform constructions of 4.8.4.8

Name	Tetraoctagonal	Truncated octaoctagonal
Image
Symmetry	[8,4] (*842)	[8,8] = [8,4,1+] (*882) =
Symbol	t{8,4}	tr{8,8}
Coxeter diagram

Dual tiling

The dual tiling, Order-8 tetrakis square tiling has face configuration V4.16.16, and represents the fundamental domains of the [8,8] symmetry group.

Symmetry

Truncated order-4 octagonal tiling with *882 mirror lines

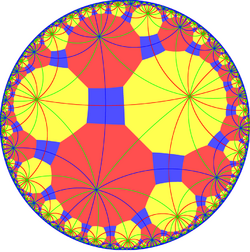
The dual of the tiling represents the fundamental domains of (*882) orbifold symmetry. From [8,8] symmetry, there are 15 small index subgroup by mirror removal and alternation operators. Mirrors can be removed if its branch orders are all even, and cuts neighboring branch orders in half. Removing two mirrors leaves a half-order gyration point where the removed mirrors met. In these images unique mirrors are colored red, green, and blue, and alternatively colored triangles show the location of gyration points. The [8⁺,8⁺], (44×) subgroup has narrow lines representing glide reflections. The subgroup index-8 group, [1⁺,8,1⁺,8,1⁺] (4444) is the commutator subgroup of [8,8].

One larger subgroup is constructed as [8,8*], removing the gyration points of (8*4), index 16 becomes (*44444444), and its direct subgroup [8,8*]⁺, index 32, (44444444).

The [8,8] symmetry can be doubled by a mirror bisecting the fundamental domain, and creating *884 symmetry.

Small index subgroups of [8,8] (*882)

Index	1	2			4
Diagram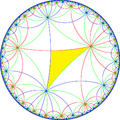
Coxeter	[8,8]	[1+,8,8] =	[8,8,1+] =	[8,1+,8] =	[1+,8,8,1+] =	[8+,8+]
Orbifold	*882	*884		*4242	*4444	44×
Semidirect subgroups
Diagram
Coxeter		[8,8+]	[8+,8]	[(8,8,2+)]	[8,1+,8,1+] = = = =	[1+,8,1+,8] = = = =
Orbifold		8*4		2*44	4*44
Direct subgroups
Index	2	4			8
Diagram
Coxeter	[8,8]+	[8,8+]+ =	[8+,8]+ =	[8,1+,8]+ =	[8+,8+]+ = [1+,8,1+,8,1+] = = =
Orbifold	882	884		4242	4444
Radical subgroups
Index		16		32
Diagram
Coxeter		[8,8*]	[8*,8]	[8,8*]+	[8*,8]+
Orbifold		*44444444		44444444

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. 

See also

• Square tiling
• Tilings of regular polygons
• List of uniform planar tilings
• List of regular polytopes

External links

• Weisstein, Eric W.. "Hyperbolic tiling". http://mathworld.wolfram.com/HyperbolicTiling.html. 
• Weisstein, Eric W.. "Poincaré hyperbolic disk". http://mathworld.wolfram.com/PoincareHyperbolicDisk.html. 
• Hyperbolic and Spherical Tiling Gallery
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• Hyperbolic Planar Tessellations, Don Hatch