Architectonic and catoptric tessellation

Short description: Uniform Euclidean 3D tessellations and their duals

The 13 architectonic or catoptric tessellations, shown as uniform cell centers, and catoptric cells, arranged as multiples of the smallest cell on top.

In geometry, John Horton Conway defines architectonic and catoptric tessellations as the uniform tessellations (or honeycombs) of Euclidean 3-space with prime space groups and their duals, as three-dimensional analogue of the Platonic, Archimedean, and Catalan tiling of the plane. The singular vertex figure of an architectonic tessellation is the dual of the cell of the corresponding catoptric tessellation, and vice versa. The cubille is the only Platonic (regular) tessellation of 3-space, and is self-dual. There are other uniform honeycombs constructed as gyrations or prismatic stacks (and their duals) which are excluded from these categories.

Enumeration

The pairs of architectonic and catoptric tessellations are listed below with their symmetry group. These tessellations only represent four symmetry space groups, and also all within the cubic crystal system. Many of these tessellations can be defined in multiple symmetry groups, so in each case the highest symmetry is expressed.

Ref. indices	Symmetry	Architectonic tessellation			Catoptric tessellation
		Name Coxeter diagram Image	Vertex figure Image	Cells	Name	Cell	Vertex figures
J11,15 A1 W1 G22 δ4	nc [4,3,4]	Cubille (Cubic honeycomb)	Octahedron,		Cubille	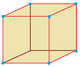Cube,
J12,32 A15 W14 G7 t1δ4	nc [4,3,4]	Cuboctahedrille (Rectified cubic honeycomb)	Cuboid,	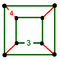	Oblate octahedrille	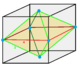Isosceles square bipyramid	,
J13 A14 W15 G8 t0,1δ4	nc [4,3,4]	Truncated cubille (Truncated cubic honeycomb)	Isosceles square pyramid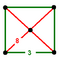		Pyramidille	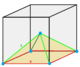Isosceles square pyramid	,
J14 A17 W12 G9 t0,2δ4	nc [4,3,4]	2-RCO-trille (Cantellated cubic honeycomb)	Wedge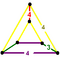	30px	Quarter oblate octahedrille	irr. Triangular bipyramid	30px , ,
J16 A3 W2 G28 t1,2δ4	bc [[4,3,4]]	Truncated octahedrille (Bitruncated cubic honeycomb)	Tetragonal disphenoid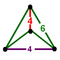		Oblate tetrahedrille	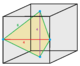Tetragonal disphenoid
J17 A18 W13 G25 t0,1,2δ4	nc [4,3,4]	n-tCO-trille (Cantitruncated cubic honeycomb)	Mirrored sphenoid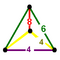	30px	Triangular pyramidille	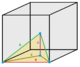Mirrored sphenoid	30px , ,
J18 A19 W19 G20 t0,1,3δ4	nc [4,3,4]	1-RCO-trille (Runcitruncated cubic honeycomb)	Trapezoidal pyramid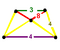	30px30px	Square quarter pyramidille	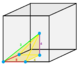Irr. pyramid	30px30px , , ,
J19 A22 W18 G27 t0,1,2,3δ4	bc [[4,3,4]]	b-tCO-trille (Omnitruncated cubic honeycomb)	Phyllic disphenoid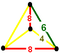		Eighth pyramidille	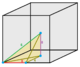Phyllic disphenoid	,
J21,31,51 A2 W9 G1 hδ4	fc [4,31,1]	Tetroctahedrille (Tetrahedral-octahedral honeycomb) or	Cuboctahedron,		Dodecahedrille or	Rhombic dodecahedron,	,
J22,34 A21 W17 G10 h2δ4	fc [4,31,1]	truncated tetraoctahedrille (Truncated tetrahedral-octahedral honeycomb) or	Rectangular pyramid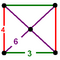	30px	Half oblate octahedrille 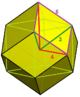or	rhombic pyramid	30px , ,
J23 A16 W11 G5 h3δ4	fc [4,31,1]	3-RCO-trille (Cantellated tetrahedral-octahedral honeycomb) or	Truncated triangular pyramid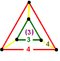	30px	Quarter cubille	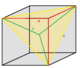80px irr. triangular bipyramid	30px
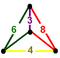
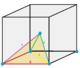J24 A20 W16 G21 h2,3δ4	fc [4,31,1]	f-tCO-trille (Cantitruncated tetrahedral-octahedral honeycomb) or	Mirrored sphenoid	30px	Half pyramidille	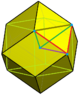Mirrored sphenoid	30px
J25,33 A13 W10 G6 qδ4	d 3[4]	Truncated tetrahedrille (Cyclotruncated tetrahedral-octahedral honeycomb) or	Isosceles triangular prism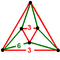		Oblate cubille	Trigonal trapezohedron

Vertex Figures

The vertex figures of all architectonic honeycombs, and the dual cells of all catoptric honeycombs are shown below, at the same scale and the same orientation:

Symmetry

These are four of the 35 cubic space groups

These four symmetry groups are labeled as:

Label	Description	space group Intl symbol	Geometric notation	Coxeter notation	Fibrifold notation
bc	bicubic symmetry or extended cubic symmetry	(221) Im3m	I43	[[4,3,4]]	8°:2
nc	normal cubic symmetry	(229) Pm3m	P43	[4,3,4]	4−:2
fc	half-cubic symmetry	(225) Fm3m	F43	[4,31,1] = [4,3,4,1+]	2−:2
d	diamond symmetry or extended quarter-cubic symmetry	(227) Fd3m	Fd4n3	3[4] = 1+,4,3,4,1+	2+:2

References

• Crystallography of Quasicrystals: Concepts, Methods and Structures by Walter Steurer, Sofia Deloudi (2009), p. 54-55. 12 packings of 2 or more uniform polyhedra with cubic symmetry

Further reading

• Conway, John H.; Burgiel, Heidi; Goodman-Strauss, Chaim (2008). "21. Naming Archimedean and Catalan Polyhedra and Tilings". The Symmetries of Things. A K Peters, Ltd.. pp. 292–298. ISBN 978-1-56881-220-5. 
• Inchbald, Guy (July 1997). "The Archimedean honeycomb duals". The Mathematical Gazette (Leicester: The Mathematical Association) 81 (491): 213–219. doi:10.2307/3619198.  [1]
• Branko Grünbaum, (1994) Uniform tilings of 3-space. Geombinatorics 4, 49 - 56.
• Norman Johnson (1991) Uniform Polytopes, Manuscript
• A. Andreini, (1905) Sulle reti di poliedri regolari e semiregolari e sulle corrispondenti reti correlative (On the regular and semiregular nets of polyhedra and on the corresponding correlative nets), Mem. Società Italiana della Scienze, Ser.3, 14 75–129. PDF [2]
• George Olshevsky, (2006) Uniform Panoploid Tetracombs, Manuscript PDF [3]
• Pearce, Peter (1980). Structure in Nature is a Strategy for Design. The MIT Press. pp. 41–47. ISBN 9780262660457. https://books.google.com/books?id=sfc2OEuE8oQC&q=%22the+tetrahedron+and+octahedron+space+filling%22. 
• Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN:978-0-471-01003-6 [4]
  • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45] See p318 [5]