Truncated tetraheptagonal tiling

Short description: Hyperbolic tiling

In geometry, the truncated tetraheptagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of tr{4,7}.

Images

Poincaré disk projection, centered on 14-gon:

Symmetry

Truncated tetraheptagonal tiling with mirror lines.

The dual to this tiling represents the fundamental domains of [7,4] (*742) symmetry. There are 3 small index subgroups constructed from [7,4] by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.

Small index subgroups of [7,4] (*742)
Index	1	2		14
Diagram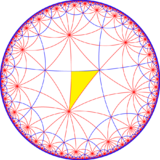
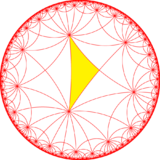
Coxeter (orbifold)	[7,4] = (*742)	[7,4,1+] = = (*772)	[7+,4] = (7*2)	[7*,4] = (*2222222)
Index	2	4		28
Diagram
Coxeter (orbifold)	[7,4]+ = (742)	[7+,4]+ = = (772)		[7*,4]+ = (2222222)

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. 

See also

• Uniform tilings in hyperbolic plane
• List of regular polytopes

External links

• Weisstein, Eric W.. "Hyperbolic tiling". http://mathworld.wolfram.com/HyperbolicTiling.html. 
• Weisstein, Eric W.. "Poincaré hyperbolic disk". http://mathworld.wolfram.com/PoincareHyperbolicDisk.html. 
• Hyperbolic and Spherical Tiling Gallery
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• Hyperbolic Planar Tessellations, Don Hatch