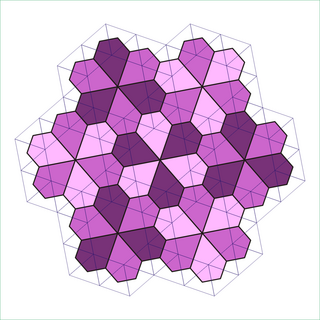
Snub trihexagonal tiling
In geometry, the snub hexagonal tiling (or snub trihexagonal tiling) is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex. It has Schläfli symbol sr{3,6}. The snub tetrahexagonal tiling is a related hyperbolic tiling with Schläfli symbol sr{4,6}.
Conway calls it a snub hextille, constructed as a snub operation applied to a hexagonal tiling (hextille).
There are three regular and eight semiregular tilings in the plane. This is the only one which does not have a reflection as a symmetry.
There is only one uniform coloring of a snub trihexagonal tiling. (Labeling the colors by numbers, "3.3.3.3.6" gives "11213".)
Circle packing
The snub trihexagonal tiling can be used as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 5 other circles in the packing (kissing number).[1] The lattice domain (red rhombus) repeats 6 distinct circles. The hexagonal gaps can be filled by exactly one circle, leading to the densest packing from the triangular tiling.
Related polyhedra and tilings

Symmetry mutations
This semiregular tiling is a member of a sequence of snubbed polyhedra and tilings with vertex figure (3.3.3.3.n) and Coxeter–Dynkin diagram ![]()
![]()
![]()
![]()
![]() . These figures and their duals have (n32) rotational symmetry, being in the Euclidean plane for n=6, and hyperbolic plane for any higher n. The series can be considered to begin with n=2, with one set of faces degenerated into digons.
. These figures and their duals have (n32) rotational symmetry, being in the Euclidean plane for n=6, and hyperbolic plane for any higher n. The series can be considered to begin with n=2, with one set of faces degenerated into digons.
6-fold pentille tiling
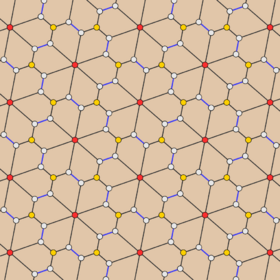
| Floret pentagonal tiling | |
|---|---|
 | |
| Type | Dual semiregular tiling |
| Faces | irregular pentagons |
| Coxeter diagram | |
| Symmetry group | p6, [6,3]+, (632) |
| Rotation group | p6, [6,3]+, (632) |
| Dual polyhedron | Snub trihexagonal tiling |
| Face configuration | V3.3.3.3.6 Face figure:  |
| Properties | face-transitive, chiral |
In geometry, the 6-fold pentille or floret pentagonal tiling is a dual semiregular tiling of the Euclidean plane.[2] It is one of the 15 known isohedral pentagon tilings. Its six pentagonal tiles radiate out from a central point, like petals on a flower.[3] Each of its pentagonal faces has four 120° and one 60° angle.
It is the dual of the uniform snub trihexagonal tiling,[4] and has rotational symmetries of orders 6-3-2 symmetry.
Variations
The floret pentagonal tiling has geometric variations with unequal edge lengths and rotational symmetry, which is given as monohedral pentagonal tiling type 5. In one limit, an edge-length goes to zero and it becomes a deltoidal trihexagonal tiling.
| General | Zero length degenerate |
Special cases | |||
|---|---|---|---|---|---|
 (See animation) |
 Deltoidal trihexagonal tiling |

|

|

|
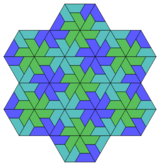
|
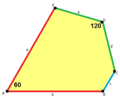 a=b, d=e A=60°, D=120° |
 a=b, d=e, c=0 A=60°, 90°, 90°, D=120° |
 a=b=2c=2d=2e A=60°, B=C=D=E=120° |
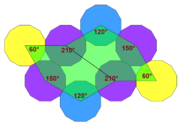 a=b=d=e A=60°, D=120°, E=150° |
 2a=2b=c=2d=2e 0°, A=60°, D=120° |
 a=b=c=d=e 0°, A=60°, D=120° |
Related k-uniform and dual k-uniform tilings
There are many k-uniform tilings whose duals mix the 6-fold florets with other tiles; for example, labeling F for V34.6, C for V32.4.3.4, B for V33.42, H for V36:
| uniform (snub trihexagonal) | 2-uniform | 3-uniform | |||
|---|---|---|---|---|---|
| F, p6 (t=3, e=3) | FH, p6 (t=5, e=7) | FH, p6m (t=3, e=3) | FCB, p6m (t=5, e=6) | FH2, p6m (t=3, e=4) | FH2, p6m (t=5, e=5) |

|

|

|

|

|

|
| dual uniform (floret pentagonal) | dual 2-uniform | dual 3-uniform | |||

|
Error creating thumbnail: Unable to save thumbnail to destination | 
|

|

|

|
| 3-uniform | 4-uniform | ||||
| FH2, p6 (t=7, e=9) | F2H, cmm (t=4, e=6) | F2H2, p6 (t=6, e=9) | F3H, p2 (t=7, e=12) | FH3, p6 (t=7, e=10) | FH3, p6m (t=7, e=8) |

|

|

|

|

|

|
| dual 3-uniform | dual 4-uniform | ||||
| Error creating thumbnail: Unable to save thumbnail to destination | 
|

|

|

|

|
Fractalization
Replacing every V36 hexagon by a rhombitrihexagon furnishes a 6-uniform tiling, two vertices of 4.6.12 and two vertices of 3.4.6.4.
Replacing every V36 hexagon by a truncated hexagon furnishes a 8-uniform tiling, five vertices of 32.12, two vertices of 3.4.3.12, and one vertex of 3.4.6.4.
Replacing every V36 hexagon by a truncated trihexagon furnishes a 15-uniform tiling, twelve vertices of 4.6.12, two vertices of 3.42.6, and one vertex of 3.4.6.4.
In each fractal tiling, every vertex in a floret pentagonal domain is in a different orbit since there is no chiral symmetry (the domains have 3:2 side lengths of in the rhombitrihexagonal; in the truncated hexagonal; and in the truncated trihexagonal).
| Rhombitrihexagonal | Truncated Hexagonal | Truncated Trihexagonal |
|---|---|---|

|

|

|

|

|

|
Related tilings
See also
- Tilings of regular polygons
- List of uniform tilings
References
- ↑ Order in Space: A design source book, Keith Critchlow, p.74-75, pattern E
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things, 2008, ISBN 978-1-56881-220-5, "A K Peters, LTD. - The Symmetries of Things". Archived from the original on 2010-09-19. https://web.archive.org/web/20100919143320/https://akpeters.com/product.asp?ProdCode=2205. Retrieved 2012-01-20. (Chapter 21, Naming Archimedean and Catalan polyhedra and tilings, p. 288, table)
- ↑ Five space-filling polyhedra by Guy Inchbald
- ↑ Weisstein, Eric W.. "Dual tessellation". http://mathworld.wolfram.com/DualTessellation.html.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 [1]
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. https://archive.org/details/isbn_0716711931. (Chapter 2.1: Regular and uniform tilings, p. 58-65)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. p. 39
- Keith Critchlow, Order in Space: A design source book, 1970, p. 69-61, Pattern R, Dual p. 77-76, pattern 5
- Dale Seymour and Jill Britton, Introduction to Tessellations, 1989, ISBN 978-0866514613, pp. 50–56, dual rosette tiling p. 96, p. 114
External links
- Weisstein, Eric W.. "Uniform tessellation". http://mathworld.wolfram.com/UniformTessellation.html.
- Weisstein, Eric W.. "Semiregular tessellation". http://mathworld.wolfram.com/SemiregularTessellation.html.
- Klitzing, Richard. "2D Euclidean tilings s3s6s - snathat - O11". https://bendwavy.org/klitzing/dimensions/flat.htm#2D.
 |