4-5 kisrhombille
| 4-5 kisrhombille | |
|---|---|
 | |
| Type | Dual semiregular hyperbolic tiling |
| Faces | Right triangle |
| Edges | Infinite |
| Vertices | Infinite |
| Coxeter diagram | |
| Symmetry group | [5,4], (*542) |
| Rotation group | [5,4]+, (542) |
| Dual polyhedron | truncated tetrapentagonal tiling |
| Face configuration | V4.8.10 |
| Properties | face-transitive |
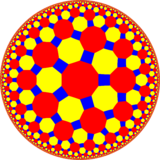
In geometry, the 4-5 kisrhombille or order-4 bisected pentagonal tiling is a semiregular dual tiling of the hyperbolic plane. It is constructed by congruent right triangles with 4, 8, and 10 triangles meeting at each vertex.
The name 4-5 kisrhombille is by Conway, seeing it as a 4-5 rhombic tiling, divided by a kis operator, adding a center point to each rhombus, and dividing into four triangles.
The image shows a Poincaré disk model projection of the hyperbolic plane.
It is labeled V4.8.10 because each right triangle face has three types of vertices: one with 4 triangles, one with 8 triangles, and one with 10 triangles.
Dual tiling
It is the dual tessellation of the truncated tetrapentagonal tiling which has one square and one octagon and one decagon at each vertex.
Related polyhedra and tilings
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN:978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
See also
- Hexakis triangular tiling
- List of uniform tilings
- Uniform tilings in hyperbolic plane
eo:Ordo-3 dusekcita seplatera kahelaro
 |