Truncated trioctagonal tiling

In geometry, the truncated trioctagonal tiling is a semiregular tiling of the hyperbolic plane. There are one square, one hexagon, and one hexadecagon (16-sides) on each vertex. It has Schläfli symbol of tr{8,3}.

Symmetry

Truncated trioctagonal tiling with mirror lines

The dual of this tiling, the order 3-8 kisrhombille, represents the fundamental domains of [8,3] (*832) symmetry. There are 3 small index subgroups constructed from [8,3] by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.

A larger index 6 subgroup constructed as [8,3^*], becomes [(4,4,4)], (*444). An intermediate index 3 subgroup is constructed as [8,3^⅄], with 2/3 of blue mirrors removed.

Small index subgroups of [8,3], (*832)

Index	1	2		3	6
Diagrams
Coxeter (orbifold)	[8,3] = (*832)	[1+,8,3] = = (*433)	[8,3+] = (3*4)	[8,3⅄] = = (*842)	[8,3*] = = (*444)
Direct subgroups
Index	2	4		6	12
Diagrams
Coxeter (orbifold)	[8,3]+ = (832)	[8,3+]+ = = (433)		[8,3⅄]+ = = (842)	[8,3*]+ = = (444)

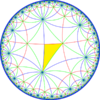
Order 3-8 kisrhombille

Truncated trioctagonal tiling
Type	Dual semiregular hyperbolic tiling
Faces	Right triangle
Edges	Infinite
Vertices	Infinite
Coxeter diagram
Symmetry group	[8,3], (*832)
Rotation group	[8,3]+, (832)
Dual polyhedron	Truncated trioctagonal tiling
Face configuration	V4.6.16
Properties	face-transitive

The order 3-8 kisrhombille is a semiregular dual tiling of the hyperbolic plane. It is constructed by congruent right triangles with 4, 6, and 16 triangles meeting at each vertex.

The image shows a Poincaré disk model projection of the hyperbolic plane.

It is labeled V4.6.16 because each right triangle face has three types of vertices: one with 4 triangles, one with 6 triangles, and one with 16 triangles. It is the dual tessellation of the truncated trioctagonal tiling which has one square and one octagon and one hexakaidecagon at each vertex.

Naming

An alternative name is 3-8 kisrhombille by Conway, seeing it as a 3-8 rhombic tiling, divided by a kis operator, adding a center point to each rhombus, and dividing into four triangles.

Related polyhedra and tilings

This tiling is one of 10 uniform tilings constructed from [8,3] hyperbolic symmetry and three subsymmetries [1⁺,8,3], [8,3⁺] and [8,3]⁺.

Uniform octagonal/triangular tilings
Symmetry: [8,3], (*832)							[8,3]+ (832)	[1+,8,3] (*443)		[8,3+] (3*4)
{8,3}	t{8,3}	r{8,3}	t{3,8}	{3,8}	rr{8,3} s2{3,8}	tr{8,3}	sr{8,3}	h{8,3}	h2{8,3}	s{3,8}
								or	or
Uniform duals
V83	V3.16.16	V3.8.3.8	V6.6.8	V38	V3.4.8.4	V4.6.16	V34.8	V(3.4)3	V8.6.6	V35.4

This tiling can be considered a member of a sequence of uniform patterns with vertex figure (4.6.2p) and Coxeter-Dynkin diagram . For p < 6, the members of the sequence are omnitruncated polyhedra (zonohedrons), shown below as spherical tilings. For p > 6, they are tilings of the hyperbolic plane, starting with the truncated triheptagonal tiling.

See also

• Tilings of regular polygons
• Hexakis triangular tiling
• List of uniform tilings
• Uniform tilings in hyperbolic plane

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. 

External links

• Weisstein, Eric W.. "Hyperbolic tiling". http://mathworld.wolfram.com/HyperbolicTiling.html. 
• Weisstein, Eric W.. "Poincaré hyperbolic disk". http://mathworld.wolfram.com/PoincareHyperbolicDisk.html. 
• Hyperbolic and Spherical Tiling Gallery
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• Hyperbolic Planar Tessellations, Don Hatch