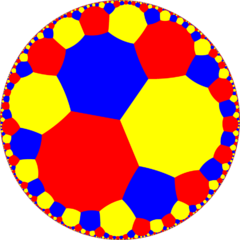
Truncated order-8 hexagonal tiling

Short description: Semiregular tiling of the hyperbolic plane

In geometry, the truncated order-8 hexagonal tiling is a semiregular tiling of the hyperbolic plane. It has Schläfli symbol of t{6,8}.

Uniform colorings

This tiling can also be constructed from *664 symmetry, as t{(6,6,4)}.

Related polyhedra and tilings

From a Wythoff construction there are fourteen hyperbolic uniform tilings that can be based from the regular order-6 octagonal tiling.

Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, there are 7 forms with full [8,6] symmetry, and 7 with subsymmetry.

Symmetry

The dual of the tiling represents the fundamental domains of (*664) orbifold symmetry. From [(6,6,4)] (*664) symmetry, there are 15 small index subgroup (11 unique) by mirror removal and alternation operators. Mirrors can be removed if its branch orders are all even, and cuts neighboring branch orders in half. Removing two mirrors leaves a half-order gyration point where the removed mirrors met. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors. The symmetry can be doubled to 862 symmetry by adding a bisecting mirror across the fundamental domains. The subgroup index-8 group, [(1⁺,6,1⁺,6,1⁺,4)] (332332) is the commutator subgroup of [(6,6,4)].

A large subgroup is constructed [(6,6,4^*)], index 8, as (4*33) with gyration points removed, becomes (*3⁸), and another large subgroup is constructed [(6,6^*,4)], index 12, as (6*32) with gyration points removed, becomes (*(32)⁶).

Small index subgroups of [(6,6,4)] (*664)

Fundamental domains
Subgroup index	1	2			4
Coxeter	[(6,6,4)]	[(1+,6,6,4)]	[(6,6,1+,4)]	[(6,1+,6,4)]	[(1+,6,6,1+,4)]	[(6+,6+,4)]
Orbifold	*664	*6362		*4343	2*3333	332×
Coxeter		[(6,6+,4)]	[(6+,6,4)]	[(6,6,4+)]	[(6,1+,6,1+,4)]	[(1+,6,1+,6,4)]
Orbifold		6*32		4*33	3*3232
Direct subgroups
Subgroup index	2	4			8
Coxeter	[(6,6,4)]+	[(1+,6,6+,4)]	[(6+,6,1+,4)]	[(6,1+,6,4+)]	[(6+,6+,4+)] = [(1+,6,1+,6,1+,4)] =
Orbifold	664	6362		4343	332332

See also

• Tilings of regular polygons
• List of uniform planar tilings

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. 

External links

• Weisstein, Eric W.. "Hyperbolic tiling". http://mathworld.wolfram.com/HyperbolicTiling.html. 
• Weisstein, Eric W.. "Poincaré hyperbolic disk". http://mathworld.wolfram.com/PoincareHyperbolicDisk.html. 
• Hyperbolic and Spherical Tiling Gallery
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• Hyperbolic Planar Tessellations, Don Hatch