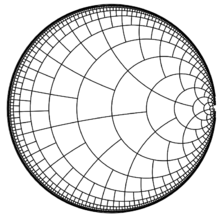
Binary tiling
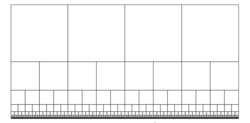
In geometry, the binary tiling (sometimes called the Böröczky tiling)[1] is a tiling of the hyperbolic plane, resembling a quadtree over the Poincaré half-plane model of the hyperbolic plane. It was first studied mathematically in 1974 by Károly Böröczky (hu).[2][3][4] However, a closely related tiling was used earlier in a 1957 print by M. C. Escher.[5]
Tiles
In one version of the tiling, the tiles are shapes bounded by three congruent horocyclic segments (two of which are part of the same horocycle), and two line segments. All tiles are congruent. In the Poincaré half-plane model, the horocyclic segments are modeled as horizontal line segments (parallel to the boundary of the half-plane) and the line segments are modeled as vertical line segments (perpendicular to the boundary of the half-plane), giving each tile the overall shape in the model of a square or rectangle. However, in the hyperbolic plane, these tiles have five sides rather than four, and are not hyperbolic polygons, because their horocyclic edges are not straight. In the half-plane model, In this model, the hyperbolic length of a horizontal horocyclic segment is its Euclidean length in the model, divided by its Euclidean distance from the half-plane boundary. Therefore, in order to make the two horocyclic segments on the lower horizontal edge of each tile each have equal length to the single horocyclic segment on the top edge of the tile, it should be placed with its top edge twice as far from the half-plane boundary as its bottom.[2]
An alternative and combinatorially equivalent version of the tiling places its vertices at the same points, but connects them by hyperbolic line segments instead of horocyclic segments, so that each tile becomes a hyperbolic convex pentagon.[6] In this form of the tiling, the tiles do not appear as rectangles in the halfplane model, and the horocycles formed by horizontal sequences of edges are replaced by apeirogons.
Enumeration and aperiodicity
There are uncountably many different tilings of the hyperbolic plane by these tiles, even when they are modified by adding protrusions and indentations to force them to meet edge-to-edge. None of these different tilings are periodic (having a cocompact symmetry group),[2][7] although some (such as the one in which there exists a line that is completely covered by tile edges) have a one-dimensional infinite symmetry group.[1]
More strongly than having all tiles the same shape, all first coronas of tiles, the set of tiles touching a single central tile, have the same pattern of tiles (up to symmetries of the hyperbolic plane allowing reflections). For tilings of the Euclidean plane, having all first coronas the same implies that the tiling is periodic and isohedral (having all tiles symmetric to each other); the binary tiling provides a strong counterexample for the corresponding property in the hyperbolic plane.[8]
Corresponding to the fact that these tilings are non-periodic but monohedral (having only one tile shape), the dual tilings of these tilings are non-periodic but monocoronal (having the same pattern of tiles surrounding each vertex). These dual tilings are formed by choosing a reference point within each tile of the binary tiling, and connecting pairs of reference points of tiles that share an edge with each other.[6]
Application
Adjusting the distance between the two vertical sides of the tiles in the binary tiling causes their area to vary, proportional to this distance. By making this distance arbitrarily small, this tiling can be used to show that the hyperbolic plane has tilings by congruent tiles of arbitrarily small area.[3]
A 1957 print by M. C. Escher, Regular Division of the Plane VI, has this tiling as its underlying structure, with each tile of the binary tiling (as seen in its quadtree form) subdivided into three right triangles. When interpreted as Euclidean shapes rather than hyperbolically, the tiles are squares and the subdivided triangles are isosceles right triangles. The print itself replaces each triangle by a stylized lizard.[5]
See also
References
- ↑ 1.0 1.1 Dolbilin, Nikolai; Frettlöh, Dirk. "Properties of Böröczky tilings in high-dimensional hyperbolic spaces". European Journal of Combinatorics 31 (4): 1181–1195. doi:10.1016/j.ejc.2009.11.016. https://www.math.uni-bielefeld.de/baake/frettloe/papers/hyp-art-final.pdf.
- ↑ 2.0 2.1 2.2 Radin, Charles (2004). "Orbits of Orbs: Sphere Packing Meets Penrose Tilings". American Mathematical Monthly 111 (2): 137–149. doi:10.2307/4145214. http://www.ma.utexas.edu/users/radin/papers/18.pdf.
- ↑ 3.0 3.1 Agol, Ian (January 26, 2018). "Smallest tile to tessellate the hyperbolic plane". MathOverflow. https://mathoverflow.net/q/291453.
- ↑ Böröczky, Károly (1974). "Gömbkitöltések állandó görbületű terekben I" (in hu). Matematikai Lapok 25: 265–306. http://real-j.mtak.hu/9373/. As cited by Radin.
- ↑ 5.0 5.1 Escher, M. C. (1989). "The regular division of the plane". Escher on Escher: Exploring the Infinite. Harry N. Abrams Inc.. pp. 90–122. ISBN 0-8109-2414-5. See especially text describing Regular Division of the Plane VI, pp. 112 & 114, schematic diagram, p. 116, and reproduction of the print, p. 117.
- ↑ 6.0 6.1 Frettlöh, Dirk; Garber, Alexey (2015). "Symmetries of monocoronal tilings". Discrete Mathematics & Theoretical Computer Science 17 (2): 203–234. doi:10.46298/dmtcs.2142.
- ↑ Penrose, R. (1979–1980). "Pentaplexity: a class of nonperiodic tilings of the plane". The Mathematical Intelligencer 2 (1): 32–37. doi:10.1007/BF03024384.
- ↑ Dolbilin, Nikolai; Schulte, Egon (June 2004). "The local theorem for monotypic tilings". Electronic Journal of Combinatorics 11 (2): Research Paper 7. doi:10.37236/1864.
 |