Physics:Pion

Short description: Lightest meson

Pion

The quark structure of the positively charged pion.
Composition	π+: ud π0: uu or dd π−: du
Statistics	Bosonic
Interactions	Strong, weak, electromagnetic, and gravity
Symbol	π+, π0, and π−
antiparticle	π+: π− π0: self
Theorized	Hideki Yukawa (1935)
Discovered	π±: César Lattes, Giuseppe Occhialini (1947), Cecil Powell π0: 1950
Types	3
Mass	π±: 139.57039(18) MeV/c2 π0: 134.9768(5) MeV/c2
mean lifetime	π±: 2.6×10−8 s π0: 8.5×10−17 s
electric charge	π±: ±1 e π0: 0 e
Charge radius	π±: ±0.659(4) fm
|u}}r charge	0
Spin	0 ħ
Isospin	π±: ±1 π0: 0
Hypercharge	0
Parity	−1
C parity	+1

In particle physics, a pion (or a pi meson, denoted with the Greek letter pi: π) is any of three subatomic particles: π⁰, π⁺, and π⁻. Each pion consists of a quark and an antiquark and is therefore a meson. Pions are the lightest mesons and, more generally, the lightest hadrons. They are unstable, with the charged pions π⁺ and π⁻ decaying after a mean lifetime of 26.033 nanoseconds (2.6033×10⁻⁸ seconds), and the neutral pion π⁰ decaying after a much shorter lifetime of 85 attoseconds (8.5×10⁻¹⁷ seconds). Charged pions most often decay into muons and muon neutrinos, while neutral pions generally decay into gamma rays.

The exchange of virtual pions, along with vector, rho and omega mesons, provides an explanation for the residual strong force between nucleons. Pions are not produced in radioactive decay, but commonly are in high-energy collisions between hadrons. Pions also result from some matter–antimatter annihilation events. All types of pions are also produced in natural processes when high-energy cosmic-ray protons and other hadronic cosmic-ray components interact with matter in Earth's atmosphere. In 2013, the detection of characteristic gamma rays originating from the decay of neutral pions in two supernova remnants has shown that pions are produced copiously after supernovas, most probably in conjunction with production of high-energy protons that are detected on Earth as cosmic rays.

The pion also plays a crucial role in cosmology, by imposing an upper limit on the energies of cosmic rays surviving collisions with the cosmic microwave background, through the Greisen–Zatsepin–Kuzmin limit.

History

An animation of the nuclear force (or residual strong force) interaction. The small colored double disks are gluons. For the choice of anticolors, see Color charge § Red, green, and blue.

Feynman diagram for the same process as in the animation, with the individual quark constituents shown, to illustrate how the fundamental strong interaction gives rise to the nuclear force. Straight lines are quarks, while multi-colored loops are gluons (the carriers of the fundamental force). Other gluons, which bind together the proton, neutron, and pion "in-flight", are not shown.
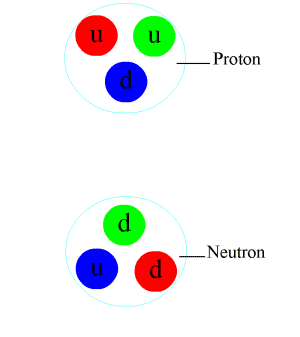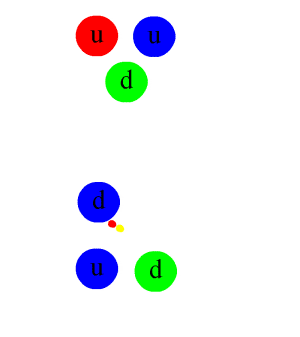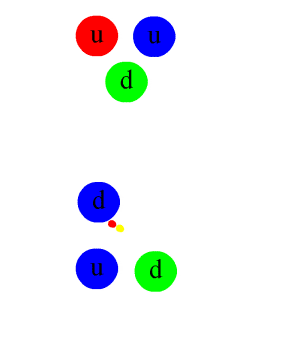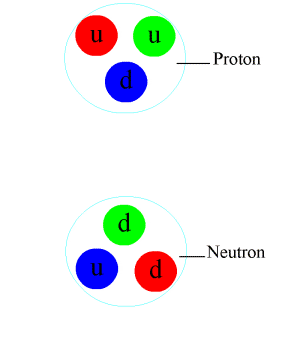
The π⁰ pion contains an anti-quark, shown to travel in the opposite direction, as per the Feynman–Stueckelberg interpretation.

Theoretical work by Hideki Yukawa in 1935 had predicted the existence of mesons as the carrier particles of the strong nuclear force. From the range of the strong nuclear force (inferred from the radius of the atomic nucleus), Yukawa predicted the existence of a particle having a mass of about 100 MeV/c². Initially after its discovery in 1936, the muon (initially called the "mu meson") was thought to be this particle, since it has a mass of 106 MeV/c². However, later experiments showed that the muon did not participate in the strong nuclear interaction. In modern terminology, this makes the muon a lepton, and not a meson. However, some communities of astrophysicists continue to call the muon a "mu-meson". The pions, which turned out to be examples of Yukawa's proposed mesons, were discovered later: the charged pions in 1947, and the neutral pion in 1950.

In 1947, the first true mesons, the charged pions, were found by the collaboration led by Cecil Powell at the University of Bristol, in England. The discovery article had four authors: César Lattes, Giuseppe Occhialini, Hugh Muirhead and Powell. Since the advent of particle accelerators had not yet come, high-energy subatomic particles were only obtainable from atmospheric cosmic rays. Photographic emulsions based on the gelatin-silver process were placed for long periods of time in sites located at high-altitude mountains, first at Pic du Midi de Bigorre in the Pyrenees, and later at Chacaltaya in the Andes Mountains, where the plates were struck by cosmic rays. After development, the photographic plates were inspected under a microscope by a team of about a dozen women. Marietta Kurz was the first person to detect the unusual "double meson" tracks, characteristic for a pion decaying into a muon, but they were too close to the edge of the photographic emulsion and deemed incomplete. A few days later, Irene Roberts observed the tracks left by pion decay that appeared in the discovery paper. Both women are credited in the figure captions in the article.

In 1948, Lattes, Eugene Gardner, and their team first artificially produced pions at the University of California's cyclotron in Berkeley, California, by bombarding carbon atoms with high-speed alpha particles. Further advanced theoretical work was carried out by Riazuddin, who in 1959 used the dispersion relation for Compton scattering of virtual photons on pions to analyze their charge radius.

Since the neutral pion is not electrically charged, it is more difficult to detect and observe than the charged pions are. Neutral pions do not leave tracks in photographic emulsions or Wilson cloud chambers. The existence of the neutral pion was inferred from observing its decay products from cosmic rays, a so-called "soft component" of slow electrons with photons. The π⁰ was identified definitively at the University of California's cyclotron in 1950 by observing its decay into two photons. Later in the same year, they were also observed in cosmic-ray balloon experiments at Bristol University.

... Yukawa choose the letter π because of its resemblance to the Kanji character for 介, which means "to mediate". Due to the concept that the meson works as a strong force mediator particle between hadrons.

Possible applications

The use of pions in medical radiation therapy, such as for cancer, was explored at a number of research institutions, including the Los Alamos National Laboratory's Meson Physics Facility, which treated 228 patients between 1974 and 1981 in New Mexico, and the TRIUMF laboratory in Vancouver, British Columbia.

Theoretical overview

In the standard understanding of the strong force interaction as defined by quantum chromodynamics, pions are loosely portrayed as Goldstone bosons of spontaneously broken chiral symmetry. That explains why the masses of the three kinds of pions are considerably less than that of the other mesons, such as the scalar or vector mesons. If their current quarks were massless particles, it could make the chiral symmetry exact and thus the Goldstone theorem would dictate that all pions have a zero mass.

In fact, it was shown by Gell-Mann, Oakes and Renner (GMOR) that the square of the pion mass is proportional to the sum of the quark masses times the quark condensate: [math]\displaystyle{ M^2_\pi=(m_u+m_d)B+\mathcal{O}(m^2) }[/math], with [math]\displaystyle{ B= \vert \langle 0\vert \bar{u}u \vert 0 \rangle /f^2_{\pi}\vert_{m_q \to 0} }[/math] the quark condensate. This is often known as the GMOR relation and it explicitly shows that [math]\displaystyle{ M_\pi=0 }[/math] in the massless quark limit. The same result also follows from Light-front holography.

Empirically, since the light quarks actually have minuscule nonzero masses, the pions also have nonzero rest masses. However, those masses are almost an order of magnitude smaller than that of the nucleons, roughly m_π ≈ √v m_q / f_π ≈ √m_q 45 MeV, where m_q are the relevant current-quark masses in MeV, around 5−10 MeV.

The pion is one of the particles that mediate the residual strong interaction between a pair of nucleons. This interaction is attractive: it pulls the nucleons together. Written in a non-relativistic form, it is called the Yukawa potential. The pion, being spinless, has kinematics described by the Klein–Gordon equation. In the terms of quantum field theory, the effective field theory Lagrangian describing the pion-nucleon interaction is called the Yukawa interaction.

The nearly identical masses of π^± and π⁰ indicate that there must be a symmetry at play: this symmetry is called the SU(2) flavour symmetry or isospin. The reason that there are three pions, π⁺, π⁻ and π⁰, is that these are understood to belong to the triplet representation or the adjoint representation 3 of SU(2). By contrast, the up and down quarks transform according to the fundamental representation 2 of SU(2), whereas the anti-quarks transform according to the conjugate representation 2*.

With the addition of the strange quark, the pions participate in a larger, SU(3), flavour symmetry, in the adjoint representation, 8, of SU(3). The other members of this octet are the four kaons and the eta meson.

Pions are pseudoscalars under a parity transformation. Pion currents thus couple to the axial vector current and so participate in the chiral anomaly.

Basic properties

Pions, which are mesons with zero spin, are composed of first-generation quarks. In the quark model, an up quark and an anti-down quark make up a π⁺, whereas a down quark and an anti-up quark make up the π⁻, and these are the antiparticles of one another. The neutral pion π⁰ is a combination of an up quark with an anti-up quark or a down quark with an anti-down quark. The two combinations have identical quantum numbers, and hence they are only found in superpositions. The lowest-energy superposition of these is the π⁰, which is its own antiparticle. Together, the pions form a triplet of isospin. Each pion has isospin (I = 1) and third-component isospin equal to its charge (I_z = +1, 0 or −1).

Charged pion decays

Feynman diagram of the dominant leptonic pion decay.

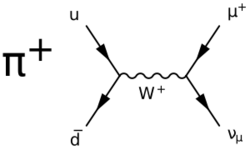
The π^± mesons have a mass of 139.6 MeV/c² and a mean lifetime of 2.6033×10⁻⁸ s. They decay due to the weak interaction. The primary decay mode of a pion, with a branching fraction of 0.999877, is a leptonic decay into a muon and a muon neutrino:

π+	→	Muon+	+	Muon neutrino
π−	→	Muon-	+	Muon antineutrino

The second most common decay mode of a pion, with a branching fraction of 0.000123, is also a leptonic decay into an electron and the corresponding electron antineutrino. This "electronic mode" was discovered at CERN in 1958:

π+	→	Positron	+	Electron neutrino
π−	→	e−	+	Electron antineutrino

The suppression of the electronic decay mode with respect to the muonic one is given approximately (up to a few percent effect of the radiative corrections) by the ratio of the half-widths of the pion–electron and the pion–muon decay reactions,

[math]\displaystyle{ R_\pi = \left(\frac{m_e}{m_\mu}\right)^2 \left(\frac{m_\pi^2 - m_e^2}{m_\pi^2 - m_\mu^2}\right)^2 = 1.283 \times 10^{-4} }[/math]

and is a spin effect known as helicity suppression.

Its mechanism is as follows: The negative pion has spin zero; therefore the lepton and the antineutrino must be emitted with opposite spins (and opposite linear momenta) to preserve net zero spin (and conserve linear momentum). However, because the weak interaction is sensitive only to the left chirality component of fields, the antineutrino has always left chirality, which means it is right-handed, since for massless anti-particles the helicity is opposite to the chirality. This implies that the lepton must be emitted with spin in the direction of its linear momentum (i.e., also right-handed). If, however, leptons were massless, they would only interact with the pion in the left-handed form (because for massless particles helicity is the same as chirality) and this decay mode would be prohibited. Therefore, suppression of the electron decay channel comes from the fact that the electron's mass is much smaller than the muon's. The electron is relatively massless compared with the muon, and thus the electronic mode is greatly suppressed relative to the muonic one, virtually prohibited.

Although this explanation suggests that parity violation is causing the helicity suppression, the fundamental reason lies in the vector-nature of the interaction which dictates a different handedness for the neutrino and the charged lepton. Thus, even a parity conserving interaction would yield the same suppression.

Measurements of the above ratio have been considered for decades to be a test of lepton universality. Experimentally, this ratio is 1.233(2)×10⁻⁴.

Beyond the purely leptonic decays of pions, some structure-dependent radiative leptonic decays (that is, decay to the usual leptons plus a gamma ray) have also been observed.

Also observed, for charged pions only, is the very rare "pion beta decay" (with branching fraction of about 10⁻⁸) into a neutral pion, an electron and an electron antineutrino (or for positive pions, a neutral pion, a positron, and electron neutrino).

π−	→	π0	+	e−	+	Electron antineutrino
π+	→	π0	+	Positron	+	Electron neutrino

The rate at which pions decay is a prominent quantity in many sub-fields of particle physics, such as chiral perturbation theory. This rate is parametrized by the pion decay constant (ƒ_π), related to the wave function overlap of the quark and antiquark, which is about 130 MeV.

Neutral pion decays

The π⁰ meson has a mass of 135.0 MeV/c² and a mean lifetime of 8.5×10⁻¹⁷ s. It decays via the electromagnetic force, which explains why its mean lifetime is much smaller than that of the charged pion (which can only decay via the weak force).

Anomaly-induced neutral pion decay.

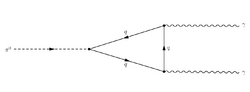
The dominant π⁰ decay mode, with a branching ratio of BR_2γ = 0.98823 , is into two photons:

π0

→

2 Gamma.

The decay π⁰ → 3Gamma (as well as decays into any odd number of photons) is forbidden by the C-symmetry of the electromagnetic interaction: The intrinsic C-parity of the π⁰ is +1, while the C-parity of a system of n photons is (−1)ⁿ.

The second largest π⁰ decay mode ( BR_γee = 0.01174 ) is the Dalitz decay (named after Richard Dalitz), which is a two-photon decay with an internal photon conversion resulting a photon and an electron-positron pair in the final state:

π0

→

γ

+

e−

+

Positron.

The third largest established decay mode ( BR_2e2e = 3.34×10⁻⁵ ) is the double-Dalitz decay, with both photons undergoing internal conversion which leads to further suppression of the rate:

π0

→

e−

+

e+

+

e−

+

e+.

The fourth largest established decay mode is the loop-induced and therefore suppressed (and additionally helicity-suppressed) leptonic decay mode ( BR_ee = 6.46×10⁻⁸ ):

π0

→

e−

+

e+.

The neutral pion has also been observed to decay into positronium with a branching fraction on the order of 10⁻⁹. No other decay modes have been established experimentally. The branching fractions above are the PDG central values, and their uncertainties are omitted, but available in the cited publication.

Pions

Particle name	Particle symbol	Antiparticle symbol	Quark content	Rest mass (MeV/c2)	IG	JPC	S	C	B'	Mean lifetime (s)	Commonly decays to (>5% of decays)
Pion	π+	π−	Up quarkDown antiquark	139.57039 ± 0.00018	1−	0−	0	0	0	2.6033 ± 0.0005 × 10−8	Antimuon + Muon neutrino
Pion	π0	Self	[math]\displaystyle{ \tfrac{\mathrm{u\bar{u}} - \mathrm{d\bar{d}}}{\sqrt 2} }[/math]	134.9768 ± 0.0005	1−	0−+	0	0	0	8.5 ± 0.2 × 10−17	Photon + Photon

^[a] ^ Make-up inexact due to non-zero quark masses.

See also

• Pionium
• Quark model
• Static forces and virtual-particle exchange
• Sanford-Wang parameterisation

Further reading

• Gerald Edward Brown and A. D. Jackson, The Nucleon-Nucleon Interaction (1976), North-Holland Publishing, Amsterdam ISBN:0-7204-0335-9

External links

• Mesons at the Particle Data Group