Socolar tiling
 There are 3 Socolar tile, a 30° rhombus, square, and a regular hexagon with tiling rules defined by the fins. |
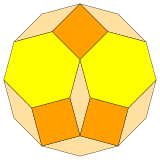 The rules of tiling can fill a regular dodecagon. |
A Socolar tiling is an example of an aperiodic tiling, developed in 1989 by Joshua Socolar in the exploration of quasicrystals.[1] There are 3 tiles a 30° rhombus, square, and regular hexagon. The 12-fold symmetry set exist similar to the 10-fold Penrose rhombic tilings, and 8-fold Ammann–Beenker tilings.[2]
The 12-fold tiles easily tile periodically, so special rules are defined to limit their connections and force nonperiodic tilings. The rhombus and square are disallowed from touching another of itself, while the hexagon can connect to both tiles as well as itself, but only in alternate edges.
Dodecagonal rhomb tiling
The dodecagonal rhomb tiling include three tiles, a 30° rhombus, a 60° rhombus, and a square.[3] And expanded set can also include an equilateral triangle, half of the 60° rhombus.60° rhombus.[4]
See also
- Pattern block - 6 tiles based on 12-fold symmetry, including the 3 Socolar tiles
- Socolar–Taylor tile - A different tiling named after Socolar
References
- ↑ Socolar, Joshua E. S. (1989), "Simple octagonal and dodecagonal quasicrystals", Physical Review B 39 (15): 10519–51, doi:10.1103/PhysRevB.39.10519, PMID 9947860, Bibcode: 1989PhRvB..3910519S
- ↑ "Tilings Encyclopedia | Socolar". https://tilings.math.uni-bielefeld.de/substitution/socolar/.
- ↑ Crystallography of Quasicrystals: Concepts, Methods and Structures, By Steurer Walter, Sofia Deloudi, pp. 40-41 [1]
- ↑ A Quasiperiodic Tiling With 12-Fold Rotational Symmetry and Inflation Factor 1 + √3 Theo P. Schaad and Peter Stampfli, 10 Feb 2021
 |




