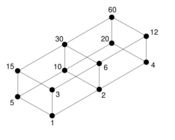
Pronic number
A pronic number is a number that is the product of two consecutive integers, that is, a number of the form [math]\displaystyle{ n(n+1). }[/math][1] The study of these numbers dates back to Aristotle. They are also called oblong numbers, heteromecic numbers,[2] or rectangular numbers;[3] however, the term "rectangular number" has also been applied to the composite numbers.[4][5]
The first few pronic numbers are:
- 0, 2, 6, 12, 20, 30, 42, 56, 72, 90, 110, 132, 156, 182, 210, 240, 272, 306, 342, 380, 420, 462 … (sequence A002378 in the OEIS).
Letting [math]\displaystyle{ P_n }[/math] denote the pronic number [math]\displaystyle{ n(n+1), }[/math] we have [math]\displaystyle{ P_{{-}n} = P_{n{-}1}. }[/math] Therefore, in discussing pronic numbers, we may assume that [math]\displaystyle{ n\geq 0 }[/math] without loss of generality, a convention that is adopted in the following sections.
As figurate numbers
The pronic numbers were studied as figurate numbers alongside the triangular numbers and square numbers in Aristotle's Metaphysics,[2] and their discovery has been attributed much earlier to the Pythagoreans.[3] As a kind of figurate number, the pronic numbers are sometimes called oblong[2] because they are analogous to polygonal numbers in this way:[1]
The nth pronic number is the sum of the first n even integers, and as such is twice the nth triangular number[1][2] and n more than the nth square number, as given by the alternative formula n2 + n for pronic numbers. The nth pronic number is also the difference between the odd square (2n + 1)2 and the (n+1)st centered hexagonal number.
Since the number of off-diagonal entries in a square matrix is twice a triangular number, it is a pronic number.[6]
Sum of pronic numbers
The partial sum of the first n positive pronic numbers is twice the value of the nth tetrahedral number:
- [math]\displaystyle{ \sum_{k=1}^{n} k(k+1) =\frac{n(n+1)(n+2)}{3}= 2T_n. }[/math]
The sum of the reciprocals of the positive pronic numbers (excluding 0) is a telescoping series that sums to 1:[7]
- [math]\displaystyle{ \sum_{i=1}^{\infty} \frac{1}{i(i+1)}=\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}\cdots=1. }[/math]
The partial sum of the first n terms in this series is[7]
- [math]\displaystyle{ \sum_{i=1}^{n} \frac{1}{i(i+1)} =\frac{n}{n+1}. }[/math]
The alternating sum of the reciprocals of the positive pronic numbers (excluding 0) is a convergent series:
- [math]\displaystyle{ \sum_{i=1}^{\infty} \frac{(-1)^{i+1}}{i(i+1)}=\frac{1}{2}-\frac{1}{6}+\frac{1}{12}-\frac{1}{20}\cdots=\log(4)-1. }[/math]
Additional properties
Pronic numbers are even, and 2 is the only prime pronic number. It is also the only pronic number in the Fibonacci sequence and the only pronic Lucas number.[8][9]
The arithmetic mean of two consecutive pronic numbers is a square number:
- [math]\displaystyle{ \frac {n(n+1) + (n+1)(n+2)}{2} = (n+1)^2 }[/math]
So there is a square between any two consecutive pronic numbers. It is unique, since
- [math]\displaystyle{ n^2 \leq n(n+1) \lt (n+1)^2 \lt (n+1)(n+2) \lt (n+2)^2. }[/math]
Another consequence of this chain of inequalities is the following property. If m is a pronic number, then the following holds:
- [math]\displaystyle{ \lfloor{\sqrt{m}}\rfloor \cdot \lceil{\sqrt{m}}\rceil = m. }[/math]
The fact that consecutive integers are coprime and that a pronic number is the product of two consecutive integers leads to a number of properties. Each distinct prime factor of a pronic number is present in only one of the factors n or n + 1. Thus a pronic number is squarefree if and only if n and n + 1 are also squarefree. The number of distinct prime factors of a pronic number is the sum of the number of distinct prime factors of n and n + 1.
If 25 is appended to the decimal representation of any pronic number, the result is a square number, the square of a number ending on 5; for example, 625 = 252 and 1225 = 352. This is so because
- [math]\displaystyle{ 100n(n+1) + 25 = 100n^2 + 100n + 25 = (10n+5)^2\, }[/math].
References
- ↑ 1.0 1.1 1.2 Conway, J. H.; Guy, R. K. (1996), The Book of Numbers, New York: Copernicus, Figure 2.15, p. 34.
- ↑ 2.0 2.1 2.2 2.3 The evolution of the Euclidean elements, Dordrecht-Boston, Mass.: D. Reidel Publishing Co., 1975, pp. 144–150, ISBN 90-277-0509-7, https://books.google.com/books?id=_1H6BwAAQBAJ&pg=PA144.
- ↑ 3.0 3.1 Ben-Menahem, Ari (2009), Historical Encyclopedia of Natural and Mathematical Sciences, Volume 1, Springer reference, Springer-Verlag, p. 161, ISBN 9783540688310, https://books.google.com/books?id=9tUrarQYhKMC&pg=PA161.
- ↑ Plutarch, De Iside et Osiride, section 42, https://www.perseus.tufts.edu/hopper/text?doc=Perseus:text:2008.01.0238:section=42, retrieved 16 April 2018
- ↑ Higgins, Peter Michael (2008), Number Story: From Counting to Cryptography, Copernicus Books, p. 9, ISBN 9781848000018, https://books.google.com/books?id=HcIwkWXy3CwC&pg=PA9.
- ↑ Rummel, Rudolf J. (1988), Applied Factor Analysis, Northwestern University Press, p. 319, ISBN 9780810108240, https://books.google.com/books?id=g_eNa_XzyEIC&pg=PA319.
- ↑ 7.0 7.1 Frantz, Marc (2010), "The telescoping series in perspective", in Diefenderfer, Caren L.; Nelsen, Roger B., The Calculus Collection: A Resource for AP and Beyond, Classroom Resource Materials, Mathematical Association of America, pp. 467–468, ISBN 9780883857618, https://books.google.com/books?id=SHJ39945R1kC&pg=PA467.
- ↑ McDaniel, Wayne L. (1998), "Pronic Lucas numbers", Fibonacci Quarterly 36 (1): 60–62, http://www.mathstat.dal.ca/FQ/Scanned/36-1/mcdaniel2.pdf, retrieved 2011-05-21.
- ↑ McDaniel, Wayne L. (1998), "Pronic Fibonacci numbers", Fibonacci Quarterly 36 (1): 56–59, http://www.fq.math.ca/Scanned/36-1/mcdaniel1.pdf.
 |