Ordered Bell number

Short description: Number of weak orderings

The 13 possible strict weak orderings on a set of three elements {a, b, c}

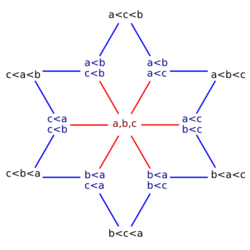
In number theory and enumerative combinatorics, the ordered Bell numbers or Fubini numbers count the number of weak orderings on a set of [math]\displaystyle{ n }[/math] elements. Weak orderings arrange their elements into a sequence allowing ties, such as might arise as the outcome of a horse race). Starting from [math]\displaystyle{ n=0 }[/math], these numbers are

1, 1, 3, 13, 75, 541, 4683, 47293, 545835, 7087261, 102247563, ... (sequence A000670 in the OEIS).

The ordered Bell numbers may be computed via a summation formula involving binomial coefficients, or by using a recurrence relation. Along with the weak orderings, they count several other types of combinatorial objects that have a bijective correspondence to the weak orderings, such as the ordered multiplicative partitions of a squarefree number or the faces of all dimensions of a permutohedron.

History

13 plane trees with ordered leaves and equal-length root-leaf paths, with the gaps between adjacent leaves labeled by the height above the leaves of the nearest common ancestor. These labels induce a weak ordering on the gaps, showing that the trees of this type are counted by the ordered Bell numbers.

The ordered Bell numbers appear in the work of (Cayley 1859), who used them to count certain plane trees with [math]\displaystyle{ n+1 }[/math] totally ordered leaves. In the trees considered by Cayley, each root-to-leaf path has the same length, and the number of nodes at distance [math]\displaystyle{ i }[/math] from the root must be strictly smaller than the number of nodes at distance [math]\displaystyle{ i+1 }[/math], until reaching the leaves. In such a tree, there are [math]\displaystyle{ n }[/math] pairs of adjacent leaves, that may be weakly ordered by the height of their lowest common ancestor; this weak ordering determines the tree. (Mor Fraenkel) call the trees of this type "Cayley trees", and they call the sequences that may be used to label their gaps (sequences of [math]\displaystyle{ n }[/math] positive integers that include at least one copy of each positive integer between one and the maximum value in the sequence) "Cayley permutations".

(Pippenger 2010) traces the problem of counting weak orderings, which has the same sequence as its solution, to the work of (Whitworth 1886). These numbers were called Fubini numbers by Louis Comtet, because they count the number of different ways to rearrange the ordering of sums or integrals in Fubini's theorem, which in turn is named after Guido Fubini. The Bell numbers, named after Eric Temple Bell, count the number of partitions of a set, and the weak orderings that are counted by the ordered Bell numbers may be interpreted as a partition together with a total order on the sets in the partition.

Formulas

Summation

The [math]\displaystyle{ n }[/math]th ordered Bell number may be given by a summation formula involving the Stirling numbers of the second kind, which count the number of partitions of an [math]\displaystyle{ n }[/math]-element set into [math]\displaystyle{ k }[/math] nonempty subsets. A weak ordering may be described as a permutation of the subsets in this partition, and so the ordered Bell numbers (the number of weak orderings) may be calculated by summing these numbers, multiplied by a factorial, [math]\displaystyle{ k! }[/math], that counts the number of these permutations: [math]\displaystyle{ a(n) = \sum_{k=0}^n k! \left\{\begin{matrix} n \\ k \end{matrix}\right\} }[/math] An alternative interpretation of the terms of this sum is that they count the features of each dimension in a permutohedron of dimension [math]\displaystyle{ n }[/math], with the [math]\displaystyle{ k }[/math]th term counting the features of dimension [math]\displaystyle{ n-k }[/math]. For instance, the three-dimensional permutohedron, the truncated octahedron, has one volume ([math]\displaystyle{ k=0 }[/math]), 14 two-dimensional faces ([math]\displaystyle{ k=1 }[/math]), 36 edges ([math]\displaystyle{ k=2 }[/math]), and 24 vertices ([math]\displaystyle{ k=3 }[/math]). The total number of these faces is 1 + 14 + 36 + 24 = 75, an ordered Bell number, corresponding to the summation formula above for [math]\displaystyle{ n=3 }[/math].

The same summation may be expanded out into a double summation involving binomial coefficients (using a formula expressing Stirling numbers as a sum of binomial coefficients), or given by an infinite series: [math]\displaystyle{ a(n) = \sum_{k=0}^n \sum_{j=0}^k (-1)^{k-j} \binom{k}{j}j^n = \frac12\sum_{m=0}^\infty\frac{m^n}{2^{m}}. }[/math]

Another summation formula expresses the ordered Bell numbers in terms of the Eulerian numbers, which count the number of permutations of [math]\displaystyle{ n }[/math] items with [math]\displaystyle{ k+1 }[/math] runs of increasing items: [math]\displaystyle{ a(n)=\sum_{k=0}^{n-1} 2^k \left\langle\begin{matrix} n \\ k \end{matrix}\right\rangle=A_n(2), }[/math] where [math]\displaystyle{ A_n }[/math] is the [math]\displaystyle{ n }[/math]th Eulerian polynomial.

Generating function and approximation

The exponential generating function of the ordered Bell numbers is [math]\displaystyle{ \sum_{n=0}^\infty a(n)\frac{x^n}{n!} = \frac{1}{1-(e^x-1)} = \frac{1}{2-e^x}. }[/math] The form of this function corresponds to the fact that the ordered Bell numbers are the numbers in the first column of the infinite matrix [math]\displaystyle{ (2I-P)^{-1} }[/math], where [math]\displaystyle{ I }[/math] is the identity matrix and [math]\displaystyle{ P }[/math] is an infinite matrix form of Pascal's triangle. Based on a contour integration of this generating function, the ordered Bell numbers can be expressed by the infinite sum [math]\displaystyle{ a(n)=\frac{n!}{2}\sum_{k=-\infty}^{\infty}(\log 2+2\pi ik)^{-(n+1)},\qquad n\ge1, }[/math] and approximated (by keeping only the [math]\displaystyle{ k=0 }[/math] term of the sum) as [math]\displaystyle{ a(n)\approx \frac{n!}{2(\log 2)^{n+1}}. }[/math]

Recurrence and modular periodicity

As well as the formulae above, the ordered Bell numbers may be calculated by the recurrence relation

[math]\displaystyle{ a(n) = \sum_{i=1}^{n}\binom{n}{i}a(n-i). }[/math]

The intuitive meaning of this formula is that a weak ordering on [math]\displaystyle{ n }[/math] items may be broken down into a choice of some nonempty set of [math]\displaystyle{ i }[/math] items that go into the first equivalence class of the ordering, together with a smaller weak ordering on the remaining [math]\displaystyle{ n-i }[/math] items. As a base case for the recurrence, [math]\displaystyle{ a(0)=1 }[/math] (there is one weak ordering on zero items). Based on this recurrence, these numbers can be shown to obey certain periodic patterns in modular arithmetic: for sufficiently large [math]\displaystyle{ n }[/math],

[math]\displaystyle{ a(n+4) \equiv a(n) \pmod{10}, }[/math]

[math]\displaystyle{ a(n+20) \equiv a(n) \pmod{100}, }[/math]

[math]\displaystyle{ a(n+100) \equiv a(n) \pmod{1000}, }[/math] and

[math]\displaystyle{ a(n+500) \equiv a(n) \pmod{10000}. }[/math]

Several additional modular identities are given by (Good 1975) and (Poonen 1988).

Additional applications

As has already been mentioned, the ordered Bell numbers count weak orderings, permutohedron faces, Cayley trees, Cayley permutations, ordered multiplicative partitions of squarefree numbers, and equivalent formulae in Fubini's theorem. Weak orderings in turn have many other applications. For instance, in horse racing, photo finishes have eliminated most but not all ties, called in this context dead heats, and the outcome of a race that may contain ties (including all the horses, not just the first three finishers) may be described using a weak ordering. For this reason, the ordered Bell numbers count the possible number of outcomes of a horse race, or the possible outcomes of a multi-candidate election. In contrast, when items are ordered or ranked in a way that does not allow ties (such as occurs with the ordering of cards in a deck of cards, or batting orders among baseball players), the number of orderings for [math]\displaystyle{ n }[/math] items is a factorial number [math]\displaystyle{ n! }[/math], which is significantly smaller than the corresponding ordered Bell number.

(Kemeny 1956) uses the ordered Bell numbers to describe the "complexity" of an n-ary relation, by which he means the number of other relations one can form from it by permuting and repeating its arguments (lowering the arity with every repetition). In this application, for each derived relation, the arguments of the original relation are weakly ordered by the positions of the corresponding arguments of the derived relation.

(Velleman Call) consider combination locks with a numeric keypad, in which several keys may be pressed simultaneously and a combination consists of a sequence of keypresses that includes each key exactly once. As they show, the number of different combinations in such a system is given by the ordered Bell numbers.

(Ellison Klein) point out an application of these numbers to optimality theory in linguistics. In this theory, grammars for natural languages are constructed by ranking certain constraints, and (in a phenomenon called factorial typology) the number of different grammars that can be formed in this way is limited to the number of permutations of the constraints. A paper reviewed by Ellison and Klein suggested an extension of this linguistic model in which ties between constraints are allowed, so that the ranking of constraints becomes a weak order rather than a total order. As they point out, the much larger magnitude of the ordered Bell numbers, relative to the corresponding factorials, allows this theory to generate a much richer set of grammars.