Ammann A1 tilings
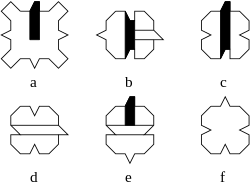
In geometry, an Ammann A1 tiling is a tiling from the 6 piece prototile set shown on the right. They were found in 1977 by Robert Ammann.[1] Ammann was inspired by the Robinsion tilings, which were found by Robinson in 1971. The A1 tiles are one of five sets of tiles discovered by Ammann and described in Tilings and Patterns.[2]
The A1 tile set is aperiodic,[2] i.e. they tile the whole Euclidean plane, but only without ever creating a periodic tiling.
Generation through matching
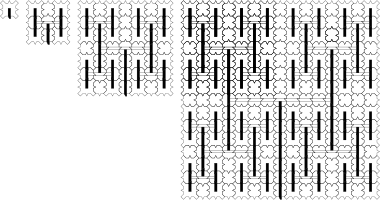
The prototiles are squares with indentations and protrusions on the sides and corners that force the tiling to form a pattern of a perfect binary tree that is continued indefinitely. The markings on the tiles in the pictures emphasize this hierarchical structure, however, they have only illustrative character and do not represent additional matching rules as this is already taken care of by the indentations and protrusions.
However, the tiling produced in this way is not unique, not even up to isometries of the Euclidean group, e.g. translations and rotations. When going to the next generation, one has choices. In the picture to the left, the initial patch in the left upper corner highlighted in blue can be prolonged by either a green or a red tile, which are mirror images of each other and instances of the prototile labeled b. Then there are two more choices in the same spirit but with prototile e. The remainder of the next generation is then fixed. If one would deviate from the pattern for this next generation, one would run into configurations that will not match up globally at least at some later stage.
The choices are encoded by infinite words from [math]\displaystyle{ \Sigma^{\omega} }[/math] for the alphabet [math]\displaystyle{ \Sigma=\{g,r\} }[/math], where g indicates the green choice while r indicates the red choice.[3] These are in bijection to a Cantor set and thus their cardinality is the continuum. Not all choices lead to a tiling of the plane. E.g. if one only sticks to the green choice one would only fill a lower right corner of the plane. If there are sufficiently generic infinitely many alteration between g and r one will however cover the whole plane. This still leaves uncountably many different A1 tilings, all of them necessarily nonperiodic. Since there are only countably many possible Euclidean isometries that respect the squares underlying the tiles to relate these different tilings, there are uncountable many A1 tilings even up to isometries.
Additionally an A1 tiling may have faults (also called corridors) going off to infinity in arms. This additionally increases the numbers of possible A1 tilings, but the cardinality remains that of the continuum. Note that the corridors allow for some part with binary tree hierarchy to be rotated compared to the other such parts.
Further pictures
See also
References
- ↑ Gardner, Martin (2001), The Colossal Book of Mathematics, W. W. Norton & Company, p. 76, ISBN 978-0393020236
- ↑ 2.0 2.1 Grünbaum, Branko; Shephard, Geoffrey C. (1986). Tilings and Patterns. New York: W. H. Freeman. ISBN 978-0-7167-1194-0.
- ↑ Grünbaum, Branko; Shephard, Geoffrey Colin (1987). Tilings and Patterns. New York: W. H. Freeman. p. 528f. ISBN 0-7167-1193-1. https://books.google.com/books?id=zY6nPwAACAAJ.
 |