Elongated triangular tiling
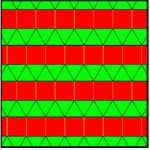
In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex. It is named as a triangular tiling elongated by rows of squares, and given Schläfli symbol {3,6}:e.
Conway calls it a isosnub quadrille.[1]
There are 3 regular and 8 semiregular tilings in the plane. This tiling is similar to the snub square tiling which also has 3 triangles and two squares on a vertex, but in a different order.
Construction
It is also the only convex uniform tiling that can not be created as a Wythoff construction. It can be constructed as alternate layers of apeirogonal prisms and apeirogonal antiprisms.
Uniform colorings
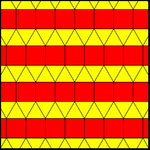
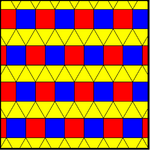
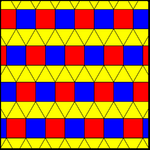
There is one uniform colorings of an elongated triangular tiling. Two 2-uniform colorings have a single vertex figure, 11123, with two colors of squares, but are not 1-uniform, repeated either by reflection or glide reflection, or in general each row of squares can be shifted around independently. The 2-uniform tilings are also called Archimedean colorings. There are infinite variations of these Archimedean colorings by arbitrary shifts in the square row colorings.
| 11122 (1-uniform) | 11123 (2-uniform or 1-Archimedean) | |
|---|---|---|
|
|
|
| cmm (2*22) | pmg (22*) | pgg (22×) |
Circle packing
The elongated triangular tiling can be used as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 5 other circles in the packing (kissing number).[2]
Related tilings
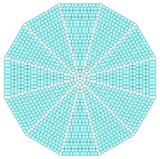
Sections of stacked triangles and squares can be combined into radial forms. This mixes two vertex configurations, 3.3.3.4.4 and 3.3.4.3.4 on the transitions. Twelve copies are needed to fill the plane with different center arrangements. The duals will mix in cairo pentagonal tiling pentagons.[3]
| Center | Triangle | Square | Hexagon | |||
|---|---|---|---|---|---|---|
| Symmetry | [3] | [3]+ | [2] | [4]+ | [6] | [6]+ |
 Tower |

|

|

|

|

|

|
 Dual |
|
|

|
|
|

|
Symmetry mutations
It is first in a series of symmetry mutations[4] with hyperbolic uniform tilings with 2*n2 orbifold notation symmetry, vertex figure 4.n.4.3.3.3, and Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
![]() . Their duals have hexagonal faces in the hyperbolic plane, with face configuration V4.n.4.3.3.3.
. Their duals have hexagonal faces in the hyperbolic plane, with face configuration V4.n.4.3.3.3.
| 4.2.4.3.3.3 | 4.3.4.3.3.3 | 4.4.4.3.3.3 |
|---|---|---|
| 2*22 | 2*32 | 2*42 |
|

|

|
There are four related 2-uniform tilings, mixing 2 or 3 rows of triangles or squares.[5][6]
| Double elongated | Triple elongated | Half elongated | One third elongated |
|---|---|---|---|

|
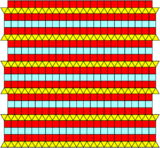
|

|

|
Prismatic pentagonal tiling
| Prismatic pentagonal tiling | |
|---|---|
 | |
| Type | Dual uniform tiling |
| Faces | irregular pentagons V3.3.3.4.4 |
| Coxeter diagram | |
| Symmetry group | cmm, [∞,2+,∞], (2*22) |
| Dual polyhedron | Elongated triangular tiling |
| Properties | face-transitive |
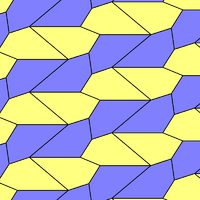
The prismatic pentagonal tiling is a dual uniform tiling in the Euclidean plane. It is one of 15 known isohedral pentagon tilings. It can be seen as a stretched hexagonal tiling with a set of parallel bisecting lines through the hexagons.
Conway calls it an iso(4-)pentille.[1] Each of its pentagonal faces has three 120° and two 90° angles.
It is related to the Cairo pentagonal tiling with face configuration V3.3.4.3.4.
Geometric variations
Monohedral pentagonal tiling type 6 has the same topology, but two edge lengths and a lower p2 (2222) wallpaper group symmetry:
|
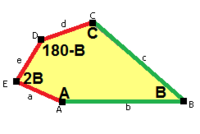 a=d=e, b=c B+D=180°, 2B=E |
Related 2-uniform dual tilings
There are four related 2-uniform dual tilings, mixing in rows of squares or hexagons (the prismatic pentagon is half-square half-hexagon).
| Dual: Double Elongated | Dual: Triple Elongated | Dual: Half Elongated | Dual: One-Third Elongated |
|---|---|---|---|

|

|

|
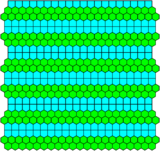
|
| Dual: [44; 33.42]1 (t=2,e=4) | Dual: [44; 33.42]2 (t=3,e=5) | Dual: [36; 33.42]1 (t=3,e=4) | Dual: [36; 33.42]2 (t=4,e=5) |
See also
- Tilings of regular polygons
- Elongated triangular prismatic honeycomb
- Gyroelongated triangular prismatic honeycomb
Notes
- ↑ 1.0 1.1 Conway, 2008, p.288 table
- ↑ Order in Space: A design source book, Keith Critchlow, p.74-75, circle pattern F
- ↑ aperiodic tilings by towers Andrew Osborne 2018
- ↑ Two Dimensional symmetry Mutations by Daniel Huson
- ↑ Chavey, D. (1989). "Tilings by Regular Polygons—II: A Catalog of Tilings". Computers & Mathematics with Applications 17: 147–165. doi:10.1016/0898-1221(89)90156-9. https://www.beloit.edu/computerscience/faculty/chavey/catalog/.
- ↑ "Uniform Tilings". http://www.uwgb.edu/dutchs/symmetry/uniftil.htm.
References
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. https://archive.org/details/isbn_0716711931. (Chapter 2.1: Regular and uniform tilings, p. 58-65)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. ISBN 0-486-23729-X. p37
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN:978-1-56881-220-5 [1]
- Keith Critchlow, Order in Space: A design source book, 1970, p. 69-61, Pattern Q2, Dual p. 77-76, pattern 6
- Dale Seymour and Jill Britton, Introduction to Tessellations, 1989, ISBN:978-0866514613, pp. 50–56
External links
- Weisstein, Eric W.. "Uniform tessellation". http://mathworld.wolfram.com/UniformTessellation.html.
- Weisstein, Eric W.. "Semiregular tessellation". http://mathworld.wolfram.com/SemiregularTessellation.html.
- Klitzing, Richard. "2D Euclidean tilings elong( x3o6o ) - etrat - O4". https://bendwavy.org/klitzing/dimensions/flat.htm#2D.
 |





