Perfect power
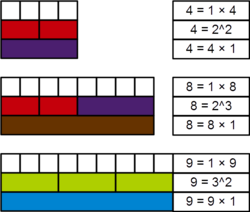
In mathematics, a perfect power is a natural number that is a product of equal natural factors, or, in other words, an integer that can be expressed as a square or a higher integer power of another integer greater than one. More formally, n is a perfect power if there exist natural numbers m > 1, and k > 1 such that mk = n. In this case, n may be called a perfect kth power. If k = 2 or k = 3, then n is called a perfect square or perfect cube, respectively. Sometimes 0 and 1 are also considered perfect powers (0k = 0 for any k > 0, 1k = 1 for any k).
Examples and sums
A sequence of perfect powers can be generated by iterating through the possible values for m and k. The first few ascending perfect powers in numerical order (showing duplicate powers) are (sequence A072103 in the OEIS):
- [math]\displaystyle{ 2^2 = 4,\ 2^3 = 8,\ 3^2 = 9,\ 2^4 = 16,\ 4^2 = 16,\ 5^2 = 25,\ 3^3 = 27, }[/math] [math]\displaystyle{ 2^5 = 32,\ 6^2 = 36,\ 7^2 = 49,\ 2^6 = 64,\ 4^3 = 64,\ 8^2 = 64, \dots }[/math]
The sum of the reciprocals of the perfect powers (including duplicates such as 34 and 92, both of which equal 81) is 1:
- [math]\displaystyle{ \sum_{m=2}^{\infty} \sum_{k=2}^{\infty}\frac{1}{m^k}=1. }[/math]
which can be proved as follows:
- [math]\displaystyle{ \sum_{m=2}^{\infty} \sum_{k=2}^{\infty}\frac{1}{m^k} =\sum_{m=2}^{\infty} \frac {1}{m^2} \sum_{k=0}^{\infty}\frac{1}{m^k} =\sum_{m=2}^{\infty} \frac {1}{m^2} \left( \frac{m}{m-1} \right) =\sum_{m=2}^{\infty} \frac {1}{m(m-1)} =\sum_{m=2}^{\infty} \left( \frac {1}{m-1} - \frac {1}{m} \right) = 1 \, . }[/math]
The first perfect powers without duplicates are:
- (sometimes 0 and 1), 4, 8, 9, 16, 25, 27, 32, 36, 49, 64, 81, 100, 121, 125, 128, 144, 169, 196, 216, 225, 243, 256, 289, 324, 343, 361, 400, 441, 484, 512, 529, 576, 625, 676, 729, 784, 841, 900, 961, 1000, 1024, ... (sequence A001597 in the OEIS)
The sum of the reciprocals of the perfect powers p without duplicates is:[1]
- [math]\displaystyle{ \sum_{p}\frac{1}{p}=\sum_{k=2}^{\infty}\mu(k)(1-\zeta(k)) \approx 0.874464368 \dots }[/math]
where μ(k) is the Möbius function and ζ(k) is the Riemann zeta function.
According to Euler, Goldbach showed (in a now-lost letter) that the sum of 1/p − 1 over the set of perfect powers p, excluding 1 and excluding duplicates, is 1:
- [math]\displaystyle{ \sum_{p}\frac{1}{p-1}= {\frac{1}{3} + \frac{1}{7} + \frac{1}{8}+ \frac{1}{15} + \frac{1}{24} + \frac{1}{26}+ \frac{1}{31}}+ \cdots = 1. }[/math]
This is sometimes known as the Goldbach–Euler theorem.
Detecting perfect powers
Detecting whether or not a given natural number n is a perfect power may be accomplished in many different ways, with varying levels of complexity. One of the simplest such methods is to consider all possible values for k across each of the divisors of n, up to [math]\displaystyle{ k \leq \log_2 n }[/math]. So if the divisors of [math]\displaystyle{ n }[/math] are [math]\displaystyle{ n_1, n_2, \dots, n_j }[/math] then one of the values [math]\displaystyle{ n_1^2, n_2^2, \dots, n_j^2, n_1^3, n_2^3, \dots }[/math] must be equal to n if n is indeed a perfect power.
This method can immediately be simplified by instead considering only prime values of k. This is because if [math]\displaystyle{ n = m^k }[/math] for a composite [math]\displaystyle{ k = ap }[/math] where p is prime, then this can simply be rewritten as [math]\displaystyle{ n = m^k = m^{ap} = (m^a)^p }[/math]. Because of this result, the minimal value of k must necessarily be prime.
If the full factorization of n is known, say [math]\displaystyle{ n = p_1^{\alpha_1}p_2^{\alpha_2} \cdots p_r^{\alpha_r} }[/math] where the [math]\displaystyle{ p_i }[/math] are distinct primes, then n is a perfect power if and only if [math]\displaystyle{ \gcd(\alpha_1, \alpha_2, \ldots, \alpha_r) \gt 1 }[/math] where gcd denotes the greatest common divisor. As an example, consider n = 296·360·724. Since gcd(96, 60, 24) = 12, n is a perfect 12th power (and a perfect 6th power, 4th power, cube and square, since 6, 4, 3 and 2 divide 12).
Gaps between perfect powers
In 2002 Romanian mathematician Preda Mihăilescu proved that the only pair of consecutive perfect powers is 23 = 8 and 32 = 9, thus proving Catalan's conjecture.
Pillai's conjecture states that for any given positive integer k there are only a finite number of pairs of perfect powers whose difference is k. This is an unsolved problem.[2]
See also
References
- Daniel J. Bernstein (1998). "Detecting perfect powers in essentially linear time". Mathematics of Computation 67 (223): 1253–1283. doi:10.1090/S0025-5718-98-00952-1. http://cr.yp.to/papers/powers-ams.pdf.
External links
 |