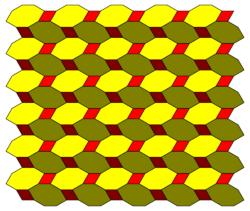
Truncated square tiling
In geometry, the truncated square tiling is a semiregular tiling by regular polygons of the Euclidean plane with one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon. It has Schläfli symbol of t{4,4}.
Conway calls it a truncated quadrille, constructed as a truncation operation applied to a square tiling (quadrille).
Other names used for this pattern include Mediterranean tiling and octagonal tiling, which is often represented by smaller squares, and nonregular octagons which alternate long and short edges.
There are 3 regular and 8 semiregular tilings in the plane.
Uniform colorings
There are two distinct uniform colorings of a truncated square tiling. (Naming the colors by indices around a vertex (4.8.8): 122, 123.)
 2 colors: 122 |
 3 colors: 123 |
Circle packing
The truncated square tiling can be used as a circle packing, placing equal diameter circles at the center of every point. Every circle is in contact with 3 other circles in the packing (kissing number).[1]
Variations

One variations on this pattern, often called a Mediterranean pattern, is shown in stone tiles with smaller squares and diagonally aligned with the borders. Other variations stretch the squares or octagons.
The Pythagorean tiling alternates large and small squares, and may be seen as topologically identical to the truncated square tiling. The squares are rotated 45 degrees and octagons are distorted into squares with mid-edge vertices.
A weaving pattern also has the same topology, with octagons flattened rectangles.
| p4m, (*442) | p4, (442) | p4g, (4*2) | pmm (*2222) | ||||
|---|---|---|---|---|---|---|---|
|
|

|

|

|

|

|

|
| p4m, (*442) | p4, (442) | cmm, (2*22) | pmm (*2222) | ||||

|

|

|

|

|

|

|

|
| Mediterranean | Pythagorean | Flemish bond | Weaving | Twisted | Rectangular/rhombic | ||
Related polyhedra and tilings

The truncated square tiling is topologically related as a part of sequence of uniform polyhedra and tilings with vertex figures 4.2n.2n, extending into the hyperbolic plane:
The 3-dimensional bitruncated cubic honeycomb projected into the plane shows two copies of a truncated tiling. In the plane it can be represented by a compound tiling, or combined can be seen as a chamfered square tiling.
 |
 |
 |
Wythoff constructions from square tiling
Drawing the tiles colored as red on the original faces, yellow at the original vertices, and blue along the original edges, all 8 forms are distinct. However treating faces identically, there are only three unique topologically forms: square tiling, truncated square tiling, snub square tiling.
- REDIRECT Template:Order 4-4 tiling table
Related tilings in other symmetries
Tetrakis square tiling
The tetrakis square tiling is the tiling of the Euclidean plane dual to the truncated square tiling. It can be constructed square tiling with each square divided into four isosceles right triangles from the center point, forming an infinite arrangement of lines. It can also be formed by subdividing each square of a grid into two triangles by a diagonal, with the diagonals alternating in direction, or by overlaying two square grids, one rotated by 45 degrees from the other and scaled by a factor of √2.
Conway calls it a kisquadrille,[2] represented by a kis operation that adds a center point and triangles to replace the faces of a square tiling (quadrille). It is also called the Union Jack lattice because of the resemblance to the UK flag of the triangles surrounding its degree-8 vertices.[3]
See also
- Tilings of regular polygons
- List of uniform tilings
- Percolation threshold
References
- ↑ Order in Space: A design source book, Keith Critchlow, p.74-75, circle pattern H
- ↑ John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 "A K Peters, LTD. - the Symmetries of Things". http://www.akpeters.com/product.asp?ProdCode=2205. (Chapter 21, Naming Archimedean and Catalan polyhedra and tilings, p288 table)
- ↑ Stephenson, John (1970), "Ising Model with Antiferromagnetic Next-Nearest-Neighbor Coupling: Spin Correlations and Disorder Points", Phys. Rev. B 1 (11): 4405–4409, doi:10.1103/PhysRevB.1.4405.
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strauss, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 [1]
- Grünbaum, Branko; Shephard, G. C. (1987). Tilings and Patterns. New York: W. H. Freeman. ISBN 0-7167-1193-1. https://archive.org/details/isbn_0716711931. (Chapter 2.1: Regular and uniform tilings, p. 58-65)
- Williams, Robert (1979). The Geometrical Foundation of Natural Structure: A Source Book of Design. Dover Publications, Inc. p. 40. ISBN 0-486-23729-X.
- Dale Seymour and Jill Britton, Introduction to Tessellations, 1989, ISBN 978-0866514613, pp. 50–56
External links
- Weisstein, Eric W.. "Semiregular tessellation". http://mathworld.wolfram.com/SemiregularTessellation.html.
- Klitzing, Richard. "2D Euclidean tilings o4x4x - tosquat - O6". https://bendwavy.org/klitzing/dimensions/flat.htm#2D.
 |