Up-and-Down Designs
Up-and-down designs (UDDs) are a family of statistical experiment designs used in dose-finding experiments in science, engineering, and medical research. Dose-finding experiments have binary responses: each individual outcome can be described as one of two possible values, such as success vs. failure or toxic vs. non-toxic. Mathematically the binary responses are coded as 1 and 0. The goal of dose-finding experiments is to estimate the strength of treatment (i.e., the "dose") that would trigger the "1" response a pre-specified proportion of the time. This dose can be envisioned as a percentile of the distribution of response thresholds. An example where dose-finding is used is in an experiment to estimate the LD50 of some toxic chemical with respect to mice.

Dose-finding designs are sequential and response-adaptive: the dose at a given point in the experiment depends upon previous outcomes, rather than be fixed a priori. Dose-finding designs are generally more efficient for this task than fixed designs, but their properties are harder to analyze, and some require specialized design software. UDDs use a discrete set of doses rather than vary the dose continuously. They are relatively simple to implement, and are also among the best understood dose-finding designs. Despite this simplicity, UDDs generate random walks with intricate properties.[1] The original UDD aimed to find the median threshold by increasing the dose one level after a "0" response, and decreasing it one level after a "1" response. Hence the name "up-and-down". Other UDDs break this symmetry in order to estimate percentiles other than the median, or are able to treat groups of subjects rather than one at a time.
UDDs were developed in the 1940s by several research groups independently.[2][3][4] The 1950s and 1960s saw rapid diversification with UDDs targeting percentiles other than the median, and expanding into numerous applied fields. The 1970s to early 1990s saw little UDD methods research, even as the design continued to be used extensively. A revival of UDD research since the 1990s has provided deeper understanding of UDDs and their properties,[5] and new and better estimation methods.[6][7]
UDDs are still used extensively in the two applications for which they were originally developed: psychophysics where they are used to estimate sensory thresholds and are often known as fixed forced-choice staircase procedures,[8] and explosive sensitivity testing, where the median-targeting UDD is often known as the Bruceton test. UDDs are also very popular in toxicity and anesthesiology research.[9] They are also considered a viable choice for Phase I clinical trials.[10]
Mathematical description
Definition
Let [math]\displaystyle{ n }[/math] be the sample size of a UDD experiment, and assuming for now that subjects are treated one at a time. Then the doses these subjects receive, denoted as random variables [math]\displaystyle{ X_1,\ldots,X_n }[/math], are chosen from a discrete, finite set of [math]\displaystyle{ M }[/math] increasing dose levels [math]\displaystyle{ \mathcal{X}=\left\{d_1,\ldots ,d_M :\ d_1 \lt \cdots \lt d_M\right\}. }[/math] Furthermore, if [math]\displaystyle{ X_i=d_m }[/math], then [math]\displaystyle{ X_{i+1}\in\{d_{m-1},d_m,d_{m+1}\}, }[/math] according to simple constant rules based on recent responses. The next subject must be treated one level up, one level down, or at the same level as the current subject. The responses themselves are denoted [math]\displaystyle{ Y_1,\ldots,Y_n \in\left\{0,1\right\}; }[/math] hereafter the "1" responses are positive and "0" negative. The repeated application of the same rules (known as dose-transition rules) over a finite set of dose levels, turns [math]\displaystyle{ X_1,\ldots,X_n }[/math] into a random walk over [math]\displaystyle{ \mathcal{X} }[/math]. Different dose-transition rules produce different UDD "flavors", such as the three shown in the figure above.
Despite the experiment using only a discrete set of dose levels, the dose-magnitude variable itself, [math]\displaystyle{ x }[/math], is assumed to be continuous, and the probability of positive response is assumed to increase continuously with increasing [math]\displaystyle{ x }[/math]. The goal of dose-finding experiments is to estimate the dose [math]\displaystyle{ x }[/math] (on a continuous scale) that would trigger positive responses at a pre-specified target rate [math]\displaystyle{ \Gamma=P\left\{Y=1\mid X=x\right\}, \ \ \Gamma\in(0,1) }[/math]; often known as the "target dose". This problem can be also expressed as estimation of the quantile [math]\displaystyle{ F^{-1}(\Gamma) }[/math] of a cumulative distribution function describing the dose-toxicity curve [math]\displaystyle{ F(x) }[/math]. The density function [math]\displaystyle{ f(x) }[/math] associated with [math]\displaystyle{ F(x) }[/math] is interpretable as the distribution of response thresholds of the population under study.
Transition probability matrix
Given that a subject receives dose [math]\displaystyle{ d_m }[/math], denote the probability that the next subject receives dose [math]\displaystyle{ d_{m-1},d_m }[/math], or [math]\displaystyle{ d_{m+1} }[/math], as [math]\displaystyle{ p_{m,m-1},p_{mm} }[/math] or [math]\displaystyle{ p_{m,m+1} }[/math], respectively. These transition probabilities obey the constraints [math]\displaystyle{ p_{m,m-1}+p_{mm}+p_{m,m+1}=1 }[/math] and the boundary conditions [math]\displaystyle{ p_{1,0}=p_{M,M+1}=0 }[/math].
Each specific set of UDD rules enables the symbolic calculation of these probabilities, usually as a function of [math]\displaystyle{ F(x) }[/math]. Assuming that transition probabilities are fixed in time, depending only upon the current allocation and its outcome, i.e., upon [math]\displaystyle{ \left(X_i,Y_i\right) }[/math] and through them upon [math]\displaystyle{ F(x) }[/math] (and possibly on a set of fixed parameters). The probabilities are then best represented via a tri-diagonal transition probability matrix (TPM) [math]\displaystyle{ \mathbf{P} }[/math]:
[math]\displaystyle{ \bf{P}=\left( \begin{array}{cccccc} p_{11}& p_{12} & 0 & \cdots & \cdots & 0 \\ p_{21} & p_{22} & p_{23} & 0 & \ddots & \vdots \\ 0 & \ddots & \ddots & \ddots & \ddots & \vdots \\ \vdots & \ddots & \ddots & \ddots & \ddots & 0 \\ \vdots & \ddots & 0 & p_{M-1,M-2} & p_{M-1,M-1} & p_{M-1,M} \\ 0 & \cdots & \cdots & 0 & p_{M,M-1} & p_{MM}\\ \end{array} \right). }[/math]
Balance point
Usually, UDD dose-transition rules bring the dose down (or at least bar it from escalating) after positive responses, and vice versa. Therefore, UDD random walks have a central tendency: dose assignments tend to meander back and forth around some dose [math]\displaystyle{ x^* }[/math] that can be calculated from the transition rules, when those are expressed as a function of [math]\displaystyle{ F(x) }[/math].[1] This dose has often been confused with the experiment's formal target [math]\displaystyle{ F^{-1}(\Gamma) }[/math], and the two are often identical - but they do not have to be. The target is the dose that the experiment is tasked with estimating, while [math]\displaystyle{ x^* }[/math], known as the "balance point", is approximately where the UDD's random walk revolves around.[11]
Stationary distribution of dose allocations
Since UDD random walks are regular Markov chains, they generate a stationary distribution of dose allocations, [math]\displaystyle{ \pi }[/math], once the effect of the manually-chosen starting dose wears off. This means, long-term visit frequencies to the various doses will approximate a steady state described by [math]\displaystyle{ \pi }[/math]. According to Markov chain theory the starting-dose effect wears off rather quickly, at a geometric rate.[12] Numerical studies suggest that it would typically take between [math]\displaystyle{ 2/M }[/math] and [math]\displaystyle{ 4/M }[/math] subjects for the effect to wear off nearly completely.[11] [math]\displaystyle{ \pi }[/math] is also the asymptotic distribution of cumulative dose allocations.
UDDs' central tendencies ensure that long-term, the most frequently visited dose (i.e., the mode of [math]\displaystyle{ \pi }[/math]) will be one of the two doses closest to the balance point [math]\displaystyle{ x^* }[/math].[1] If [math]\displaystyle{ x^* }[/math] is outside the range of allowed doses, then the mode will be on the boundary dose closest to it. Under the original median-finding UDD, the mode will be at the closest dose to [math]\displaystyle{ x^* }[/math] in any case. Away from the mode, asymptotic visit frequencies decrease sharply, at a faster-than-geometric rate. Even though a UDD experiment is still a random walk, long excursions away from the region of interest are very unlikely.
Common UDDs
Original ("simple" or "classical") UDD
The original "simple" or "classical" UDD moves the dose up one level upon a negative response, and vice versa. Therefore, the transition probabilities are [math]\displaystyle{ \begin{array}{rl} p_{m,m+1}&=P\{Y_i=0|X_i=d_m\}=1-F(d_m);\\ p_{m,m-1}&=P\{Y_i=1|X_i=d_m\}=F(d_m). \end{array} }[/math]
We use the original UDD as an example for calculating the balance point [math]\displaystyle{ x^* }[/math]. The design's 'up', 'down' functions are [math]\displaystyle{ p(x)=1-F(x),q(x)=F(x). }[/math] We equate them to find [math]\displaystyle{ F^* }[/math]: [math]\displaystyle{ 1-F^*=F^*\ \longrightarrow \ F^*=0.5. }[/math] The "classical" UDD is designed to find the median threshold. This is a case where [math]\displaystyle{ F^*=\Gamma. }[/math]
The "classical" UDD can be seen as a special case of each of the more versatile designs described below.
Durham and Flournoy's biased coin design
This UDD shifts the balance point, by adding the option of treating the next subject at the same dose rather than move only up or down. Whether to stay is determined by a random toss of a metaphoric "coin" with probability [math]\displaystyle{ b=P\{\textrm{heads}\}. }[/math] This biased-coin design (BCD) has two "flavors", one for [math]\displaystyle{ F^*\gt 0.5 }[/math] and one for [math]\displaystyle{ F^*\lt 0.5, }[/math] whose rules are shown below:
[math]\displaystyle{ X_{i+1} = \begin{array}{ll} d_{m+1} & \textrm{if }\ \ Y_i=0\ \ \&\ \ \textrm{ 'heads'};\\ d_{m-1} & \textrm{if }\ \ Y\_i=1;\\ d_m & \textrm{if }\ \ Y_i=0\ \ \& \ \ \textrm{ 'tails'}.\\ \end{array} }[/math]
The heads probability [math]\displaystyle{ b }[/math] can take any value in[math]\displaystyle{ [0,1] }[/math]. The balance point is [math]\displaystyle{ \begin{array}{rcl} b\left(1-F^*\right) &=& F^*\\ F^* &=& \frac{b}{1+b}\in[0,0.5]. \end{array} }[/math]
The BCD balance point can made identical to a target rate [math]\displaystyle{ F^{-1}(\Gamma) }[/math] by setting the heads probability to [math]\displaystyle{ b=\Gamma/(1-\Gamma) }[/math]. For example, for [math]\displaystyle{ \Gamma=0.3 }[/math] set [math]\displaystyle{ b=3/7 }[/math]. Setting [math]\displaystyle{ b=1 }[/math] makes this design identical to the classical UDD, and inverting the rules by imposing the coin toss upon positive rather than negative outcomes, produces above-median balance points. Versions with two coins, one for each outcome, have also been published, but they do not seem to offer an advantage over the simpler single-coin BCD.
Group (cohort) UDDs
Some dose-finding experiments, such as phase I trials, require a waiting period of weeks before determining each individual outcome. It may preferable then, to be able treat several subjects at once or in rapid succession. With group UDDs, the transition rules apply rules to cohorts of fixed size [math]\displaystyle{ s }[/math] rather than to individuals. [math]\displaystyle{ X_i }[/math] becomes the dose given to cohort [math]\displaystyle{ i }[/math], and [math]\displaystyle{ Y_i }[/math] is the number of positive responses in the [math]\displaystyle{ i }[/math]-th cohort, rather than a binary outcome. Given that the [math]\displaystyle{ i }[/math]-th cohort is treated at [math]\displaystyle{ X_i=d_m }[/math] on the interior of [math]\displaystyle{ \mathcal{X} }[/math] the [math]\displaystyle{ i+1 }[/math]-th cohort is assigned to
[math]\displaystyle{ X_{i+1}= \begin{cases} d_{m+1} &\textrm{if}\ \ Y_i\le l;\\ d_{m-1} &\textrm{if}\ \ Y_i\ge u;\\ d_m &\textrm{if}\ \ Y_i\lt u. \end{cases} }[/math]
[math]\displaystyle{ Y_i }[/math] follow a binomial distribution conditional on [math]\displaystyle{ X_i }[/math], with parameters[math]\displaystyle{ s }[/math] and[math]\displaystyle{ F(X_i) }[/math]. The up and down probabilities are the binomial distribution's tails, and the stay probability its center (it is zero if [math]\displaystyle{ u=l+1 }[/math]). A specific choice of parameters can be abbreviated as GUD[math]\displaystyle{ _{(s,l,u)}. }[/math]
Nominally, group UDDs generate [math]\displaystyle{ s }[/math]-order random walks, since the [math]\displaystyle{ s }[/math] most recent observations are needed to determine the next allocation. However, with cohorts viewed as single mathematical entities, these designs generate a first-order random walk having a tri-diagonal TPM as above. Some relevant group UDD subfamilies:
- Symmetric designs with [math]\displaystyle{ l+u=s }[/math] (e.g., GUD[math]\displaystyle{ _{(2,0,2)} }[/math]) target the median.
- The family GUD[math]\displaystyle{ _{(s,0,1)}, }[/math] encountered in toxicity studies, allows escalation only with zero positive responses, and de-escalate upon any positive response. The escalation probability at [math]\displaystyle{ x }[/math] is [math]\displaystyle{ \left(1-F(x)\right)^s, }[/math] and since this design does not allow for remaining at the same dose, at the balance point it will be exactly [math]\displaystyle{ 1/2 }[/math]. Therefore,
[math]\displaystyle{ F^*=1-\left(\frac {1}{2}\right)^{1/s}. }[/math]
With [math]\displaystyle{ s=2,3,4 }[/math] would be associated with [math]\displaystyle{ F^*\approx 0.293,0.206 }[/math] and [math]\displaystyle{ 0.159 }[/math], respectively. The mirror-image family GUD[math]\displaystyle{ _{(s,s-1,s)} }[/math] has its balance points at one minus these probabilities.
For general group UDDs, the balance point can be calculated only numerically, by finding the dose [math]\displaystyle{ x^* }[/math] with toxicity rate [math]\displaystyle{ F^* }[/math] such that
[math]\displaystyle{ \sum_{r=u}^s \left(\begin{array}{c} s\\ r\\ \end{array}\right) \left(F^*\right)^r(1-F^*)^{s-r}= \sum_{t=0}^{l} \left(\begin{array}{c} s\\ t\\ \end{array}\right) \left(F^*\right)^t(1-F^*)^{s-t}. }[/math]
Any numerical root-finding algorithm, e.g., Newton–Raphson, can be used to solve for [math]\displaystyle{ F^* }[/math].[13]
[math]\displaystyle{ k }[/math]-in-a-row (or "transformed" or "geometric") UDD
This is the most commonly used non-median UDD. It was introduced by Wetherill in 1963,[14] and proliferated by him and colleagues shortly thereafter to psychophysics,[15] where it remains one of the standard methods to find sensory thresholds.[8] Wetherill called it "transformed" UDD; Gezmu who was the first to analyze its random-walk properties, called it "Geometric" UDD in the 1990s;[16] and in the 2000s the more straightforward name "[math]\displaystyle{ k }[/math]-in-a-row" UDD was adopted.[11] The design's rules are deceptively simple:
[math]\displaystyle{ X_{i+1}= \begin{cases} d_{m+1} &\textrm{if}\ \ Y_{i-k+1}=\cdots=Y_i=0,\ \ \textrm{ all}\ \textrm{observed}\ \textrm{at}\ \ d_m;\\ d_{m-1} &\textrm{if}\ \ Y_i=1; \\ d_m &\textrm{otherwise}, \end{cases} }[/math]
Every dose escalation requires [math]\displaystyle{ k }[/math] non-toxicities observed on consecutive data points, all at the current dose, while de-escalation only requires a single toxicity. It closely resembles GUD[math]\displaystyle{ _{(s,0,1)} }[/math] described above, and indeed shares the same balance point. The difference is that [math]\displaystyle{ k }[/math]-in-a-row can bail out of a dose level upon the first toxicity, whereas its group UDD sibling might treat the entire cohort at once, and therefore might see more than one toxicity before descending.
The method used in sensory studies is actually the mirror-image of the one defined above, with [math]\displaystyle{ k }[/math] successive responses required for a de-escalation and only one non-response for escalation, yielding [math]\displaystyle{ F^*\approx 0.707,0.794,0.841,\ldots }[/math] for [math]\displaystyle{ k=2,3,4,\ldots }[/math].[17]
[math]\displaystyle{ k }[/math]-in-a-row generates a [math]\displaystyle{ k }[/math]-th order random walk because knowledge of the last [math]\displaystyle{ k }[/math] responses might be needed. It can be represented as a first-order chain with [math]\displaystyle{ Mk }[/math] states, or as a Markov chain with [math]\displaystyle{ M }[/math] levels, each having [math]\displaystyle{ k }[/math] internal states labeled [math]\displaystyle{ 0 }[/math] to [math]\displaystyle{ k-1 }[/math] The internal state serves as a counter of the number of immediately recent consecutive non-toxicities observed at the current dose. This description is closer to the physical dose-allocation process, because subjects at different internal states of the level [math]\displaystyle{ m }[/math], are all assigned the same dose [math]\displaystyle{ d_m }[/math]. Either way, the TPM is [math]\displaystyle{ Mk\times Mk }[/math] (or more precisely, [math]\displaystyle{ \left[(M-1)k+1)\right]\times \left[(M-1)k+1)\right] }[/math], because the internal counter is meaningless at the highest dose) - and it is not tridiagonal.
Here is the expanded [math]\displaystyle{ k }[/math]-in-a-row TPM with [math]\displaystyle{ k=2 }[/math] and [math]\displaystyle{ M=5 }[/math], using the abbreviation [math]\displaystyle{ F_m\equiv F\left(d_m\right). }[/math] Each level's internal states are adjacent to each other.
- [math]\displaystyle{ \begin{bmatrix} F_1 & 1-F_1 & 0 & 0 & 0 & 0 & 0 & 0 & 0\\ F_1 & 0 & 1-F_1 & 0 & 0 & 0 & 0 & 0 & 0\\ F_2 & 0 & 0 & 1-F_2 & 0 & 0 & 0 & 0 & 0 \\ F_2 & 0 & 0 & 0 & 1-F_2 & 0 & 0 & 0 & 0 \\ 0 & 0 & F_3 & 0 & 0 &1-F_3 & 0 & 0 & 0 \\ 0 & 0 & F_3 & 0 & 0 & 0 & 1-F_3 & 0 & 0 \\ 0 & 0 & 0 & 0 & F_4 & 0 & 0 &1-F_4 & 0 \\ 0 & 0 & 0 & 0 & F_4 & 0 & 0 & 0 & 1-F_4 \\ 0 & 0 & 0 & 0 & 0 & 0 & F_5 & 0 & 1-F_5 \\ \end{bmatrix}. }[/math]
[math]\displaystyle{ k }[/math]-in-a-row is often considered for clinical trials targeting a low-toxicity dose. In this case, the balance point and the target are not identical; rather, [math]\displaystyle{ k }[/math] is chosen to aim close to the target rate, e.g., [math]\displaystyle{ k=2 }[/math] for studies targeting the 30th percentile, and [math]\displaystyle{ k=3 }[/math] for studies targeting the 20th percentile.
Estimating the target dose
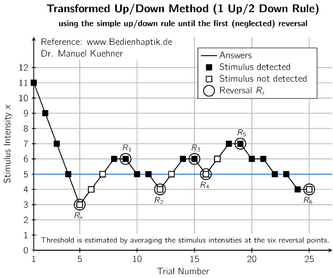
Unlike other design approaches, UDDs do not have a specific estimation method "bundled in" with the design as a default choice. Historically, the more common choice has been some weighted average of the doses administered, usually excluding the first few doses to mitigate the starting-point bias. This approach antedates deeper understanding of UDDs' Markov properties, but its success in numerical evaluations relies upon the eventual sampling from [math]\displaystyle{ \pi }[/math], since the latter is centered roughly around [math]\displaystyle{ x^*. }[/math][5]
The single most popular among these averaging estimators was introduced by Wetherill et al. in 1966, and only includes reversal points (points where the outcome switches from 0 to 1 or vice versa) in the average.[18]In recent years, the limitations of averaging estimators have come to light, in particular the many sources of bias that are very difficult to mitigate. Reversal estimators suffer from both multiple biases (although there is some inadvertent cancelling out of biases), and increased variance due to using a subsample of doses. However, the knowledge about averaging-estimator limitations has yet to disseminate outside the methodological literature and affect actual practice.[5]
By contrast, regression estimators attempt to approximate the curve [math]\displaystyle{ y=F(x) }[/math] describing the dose-response relationship, in particular around the target percentile. The raw data for the regression are the doses [math]\displaystyle{ d_m }[/math] on the horizontal axis, and the observed toxicity frequencies, [math]\displaystyle{ \hat{F}_m=\frac{\sum_{i=1}^n Y_iI\left[X_i=d_m\right]}{\sum_{i=1}^n I\left[X_i=d_m\right]},\ m=1,\ldots,M, }[/math] on the vertical axis. The target estimate is the abscissa of the point where the fitted curve crosses [math]\displaystyle{ y=\Gamma. }[/math]
Probit regression has been used for many decades to estimate UDD targets, although far less commonly than the reversal-averaging estimator. In 2002, Stylianou and Flournoy introduced an interpolated version of isotonic regression (IR) to estimate UDD targets and other dose-response data.[6] More recently, a modification called "centered isotonic regression" (CIR) was developed by Oron and Flournoy, promising substantially better estimation performance than ordinary isotonic regression in most cases, and also offering the first viable interval estimator for isotonic regression in general.[7] Isotonic regression estimators appear to be the most compatible with UDDs, because both approaches are nonparametric and relatively robust.[5] The publicly available R package "cir" implements both CIR and IR for dose-finding and other applications.[19]
References
- ↑ 1.0 1.1 1.2 Durham, SD; Flournoy, N. "Up-and-down designs. I. Stationary treatment distributions.". in Flournoy, N; Rosenberger, WF. IMS Lecture Notes Monograph Series. 25: Adaptive Designs. pp. 139–157.
- ↑ Dixon, WJ; Mood, AM (1948). "A method for obtaining and analyzing sensitivity data". Journal of the American Statistical Association 43 (241): 109–126. doi:10.1080/01621459.1948.10483254.
- ↑ von Békésy, G (1947). "A new audiometer". Acta Oto-Laryngologica 35 (5–6): 411–422. doi:10.3109/00016484709123756.
- ↑ Anderson, TW; McCarthy, PJ; Tukey, JW (1946). 'Staircase' method of sensitivity testing (Technical report). Naval Ordnance Report. 65-46.
- ↑ 5.0 5.1 5.2 5.3 Flournoy, N; Oron, AP. Dean, A. ed. Handbook of Design and Analysis of Experiments. CRC Press. pp. 858–894.
- ↑ 6.0 6.1 Stylianou, MP; Flournoy, N (2002). "Dose finding using the biased coin up-and-down design and isotonic regression". Biometrics 58 (1): 171–177. doi:10.1111/j.0006-341x.2002.00171.x. PMID 11890313.
- ↑ 7.0 7.1 Oron, AP; Flournoy, N (2017). "Centered Isotonic Regression: Point and Interval Estimation for Dose-Response Studies". Statistics in Biopharmaceutical Research 9 (3): 258–267. doi:10.1080/19466315.2017.1286256.
- ↑ 8.0 8.1 Leek, MR (2001). "Adaptive procedures in psychophysical research". Perception and Psychophysics 63 (8): 1279–1292. doi:10.3758/bf03194543. PMID 11800457.
- ↑ Pace, NL; Stylianou, MP (2007). "Advances in and Limitations of Up-and-down Methodology: A Precis of Clinical Use, Study Design, and Dose Estimation in Anesthesia Research". Anesthesiology 107: 144–152. doi:10.1097/01.anes.0000267514.42592.2a. PMID 17585226.
- ↑ Oron, AP; Hoff, PD (2013). "Small-Sample Behavior of Novel Phase I Cancer Trial Designs". Clinical Trials 10 (1): 63–80. doi:10.1177/1740774512469311. PMID 23345304.
- ↑ 11.0 11.1 11.2 Oron, AP; Hoff, PD (2009). "The k-in-a-row up-and-down design, revisited". Statistics in Medicine 28 (13): 1805–1820. doi:10.1002/sim.3590. PMID 19378270.
- ↑ Diaconis, P; Stroock, D (1991). "Geometric bounds for eigenvalues of Markov chain". The Annals of Applied Probability 1: 36–61. doi:10.1214/aoap/1177005980.
- ↑ Gezmu, M; Flournoy, N (2006). "Group up-and-down designs for dose-finding". Journal of Statistical Planning and Inference 136 (6): 1749–1764. doi:10.1016/j.jspi.2005.08.002.
- ↑ Wetherill, GB; Levitt, H (1963). "Sequential estimation of quantal response curves". Journal of the Royal Statistical Society, Series B 25: 1–48. doi:10.1111/j.2517-6161.1963.tb00481.x.
- ↑ Wetherill, GB (1965). "Sequential estimation of points on a Psychometric Function". British Journal of Mathematical and Statistical Psychology 18: 1–10. doi:10.1111/j.2044-8317.1965.tb00689.x. PMID 14324842.
- ↑ Gezmu, Misrak (1996). The Geometric Up-and-Down Design for Allocating Dosage Levels (PhD). American University.
- ↑ Garcia-Perez, MA (1998). "Forced-choice staircases with fixed step sizes: asymptotic and small-sample properties". Vision Research 38 (12): 1861–81. doi:10.1016/s0042-6989(97)00340-4. PMID 9797963.
- ↑ Wetherill, GB; Chen, H; Vasudeva, RB (1966). "Sequential estimation of quantal response curves: a new method of estimation". Biometrika 53 (3–4): 439–454. doi:10.1093/biomet/53.3-4.439.
- ↑ Oron, Assaf. "Package 'cir'". R Foundation for Statistical Computing. https://cran.r-project.org/web/packages/cir/index.html.


