Blocking (statistics)
In the statistical theory of the design of experiments, blocking is the arranging of experimental units that are similar to one another in groups (blocks) based on one or more variables. These variables are chosen carefully to minimize the impact of their variability on the observed outcomes. There are different ways that blocking can be implemented, resulting in different confounding effects. However, the different methods share the same purpose: to control variability introduced by specific factors that could influence the outcome of an experiment. The roots of blocking originated from the statistician, Ronald Fisher, following his development of ANOVA.[1]
History
The use of blocking in experimental design has an evolving history that spans multiple disciplines. The foundational concepts of blocking date back to the early 20th century with statisticians like Ronald A. Fisher. His work in developing analysis of variance (ANOVA) set the groundwork for grouping experimental units to control for extraneous variables. Blocking evolved over the years, leading to the formalization of randomized block designs and Latin square designs.[1]Today, blocking still plays a pivotal role in experimental design, and in recent years, advancements in statistical software and computational capabilities have allowed researchers to explore more intricate blocking designs.
Use
Blocking reduces unexplained variability. Its principle lies in the fact that variability which cannot be overcome (e.g. needing two batches of raw material to produce 1 container of a chemical) is confounded or aliased with a(n) (higher/highest order) interaction to eliminate its influence on the end product.[2] High order interactions are usually of the least importance (think of the fact that temperature of a reactor or the batch of raw materials is more important than the combination of the two – this is especially true when more (3, 4, ...) factors are present); thus it is preferable to confound this variability with the higher interaction.[2]
Examples
- Male and female: An experiment is designed to test a new drug on patients. There are two levels of the treatment, drug, and placebo, administered to male and female patients in a double blind trial. The sex of the patient is a blocking factor accounting for treatment variability between males and females. This reduces sources of variability and thus leads to greater precision.
- Elevation: An experiment is designed to test the effects of a new pesticide on a specific patch of grass. The grass area contains a major elevation change and thus consists of two distinct regions – 'high elevation' and 'low elevation'. A treatment group (the new pesticide) and a placebo group are applied to both the high elevation and low elevation areas of grass. In this instance the researcher is blocking the elevation factor which may account for variability in the pesticide's application.
- Intervention: Suppose a process is invented that intends to make the soles of shoes last longer, and a plan is formed to conduct a field trial. Given a group of n volunteers, one possible design would be to give n/2 of them shoes with the new soles and n/2 of them shoes with the ordinary soles, randomizing the assignment of the two kinds of soles. This type of experiment is a completely randomized design. Both groups are then asked to use their shoes for a period of time, and then measure the degree of wear of the soles. This is a workable experimental design, but purely from the point of view of statistical accuracy (ignoring any other factors), a better design would be to give each person one regular sole and one new sole, randomly assigning the two types to the left and right shoe of each volunteer. Such a design is called a "randomized complete block design." This design will be more sensitive than the first, because each person is acting as his/her own control and thus the control group is more closely matched to the treatment group block design
Nuisance variables
In the examples listed above, a nuisance variable is a variable that is not the primary focus of the study but can affect the outcomes of the experiment.[3] They are considered potential sources of variability that, if not controlled or accounted for, may confound the interpretation between the independent and dependent variables.
To address nuisance variables, researchers can employ different methods such as blocking or randomization. Blocking involves grouping experimental units based on levels of the nuisance variable to control for its influence. Randomization helps distribute the effects of nuisance variables evenly across treatment groups.
By using one of these methods to account for nuisance variables, researchers can enhance the internal validity of their experiments, ensuring that the effects observed are more likely attributable to the manipulated variables rather than extraneous influences.
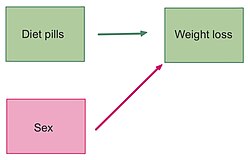
In the first example provided above, the sex of the patient would be a nuisance variable. For example, consider if the drug was a diet pill and the researchers wanted to test the effect of the diet pills on weight loss. The explanatory variable is the diet pill and the response variable is the amount of weight loss. Although the sex of the patient is not the main focus of the experiment—the effect of the drug is—it is possible that the sex of the individual will affect the amount of weight lost.
Blocking used for nuisance factors that can be controlled
In the statistical theory of the design of experiments, blocking is the arranging of experimental units in groups (blocks) that are similar to one another. Typically, a blocking factor is a source of variability that is not of primary interest to the experimenter.[3][4]
When studying probability theory the blocks method consists of splitting a sample into blocks (groups) separated by smaller subblocks so that the blocks can be considered almost independent.[5] The blocks method helps proving limit theorems in the case of dependent random variables.
The blocks method was introduced by S. Bernstein:[6] The method was successfully applied in the theory of sums of dependent random variables and in extreme value theory.[7][8][9]
Example
In our previous diet pills example, a blocking factor could be the sex of a patient. We could put individuals into one of two blocks (male or female). And within each of the two blocks, we can randomly assign the patients to either the diet pill (treatment) or placebo pill (control). By blocking on sex, this source of variability is controlled, therefore, leading to greater interpretation of how the diet pills affect weight loss.
Definition of blocking factors
A nuisance factor is used as a blocking factor if every level of the primary factor occurs the same number of times with each level of the nuisance factor.[3] The analysis of the experiment will focus on the effect of varying levels of the primary factor within each block of the experiment.
Block a few of the most important nuisance factors
The general rule is:
- "Block what you can; randomize what you cannot."[3]
Blocking is used to remove the effects of a few of the most important nuisance variables. Randomization is then used to reduce the contaminating effects of the remaining nuisance variables. For important nuisance variables, blocking will yield higher significance in the variables of interest than randomizing.[10]
Implementation
Implementing blocking in experimental design involves a series of steps to effectively control for extraneous variables and enhance the precision of treatment effect estimates.
Identify nuisance variables
Identify potential factors that are not the primary focus of the study but could introduce variability.
Select appropriate blocking factors
Carefully choose blocking factors based on their relevance to the study as well as their potential to confound the primary factors of interest.[11]
Define block sizes
There are consequences to partitioning a certain sized experiment into a certain number of blocks as the number of blocks determines the number of confounded effects.[12]
Assign treatments to blocks
You may choose to randomly assign experimental units to treatment conditions within each block which may help ensure that any unaccounted for variability is spread evenly across treatment groups. However, depending on how you assign treatments to blocks, you may obtain a different number of confounded effects.[4] Therefore, the number of as well as which specific effects get confounded can be chosen which means that assigning treatments to blocks is superior over random assignment.[4]
Replication
By running a different design for each replicate, where a different effect gets confounded each time, the interaction effects are partially confounded instead of completely sacrificing one single effect.[4] Replication enhances the reliability of results and allows for a more robust assessment of treatment effects.[12]
Example
Table
One useful way to look at a randomized block experiment is to consider it as a collection of completely randomized experiments, each run within one of the blocks of the total experiment.[3]
| Name of design | Number of factors k | Number of runs n |
|---|---|---|
| 2-factor RBD | 2 | L1 * L2 |
| 3-factor RBD | 3 | L1 * L2 * L3 |
| 4-factor RBD | 4 | L1 * L2 * L3 * L4 |
| [math]\displaystyle{ \vdots }[/math] | [math]\displaystyle{ \vdots }[/math] | [math]\displaystyle{ \vdots }[/math] |
| k-factor RBD | k | L1 * L2 * [math]\displaystyle{ \cdots }[/math] * Lk |
with
- L1 = number of levels (settings) of factor 1
- L2 = number of levels (settings) of factor 2
- L3 = number of levels (settings) of factor 3
- L4 = number of levels (settings) of factor 4
- [math]\displaystyle{ \vdots }[/math]
- Lk = number of levels (settings) of factor k
Example
Suppose engineers at a semiconductor manufacturing facility want to test whether different wafer implant material dosages have a significant effect on resistivity measurements after a diffusion process taking place in a furnace. They have four different dosages they want to try and enough experimental wafers from the same lot to run three wafers at each of the dosages.
The nuisance factor they are concerned with is "furnace run" since it is known that each furnace run differs from the last and impacts many process parameters.
An ideal way to run this experiment would be to run all the 4x3=12 wafers in the same furnace run. That would eliminate the nuisance furnace factor completely. However, regular production wafers have furnace priority, and only a few experimental wafers are allowed into any furnace run at the same time.
A non-blocked way to run this experiment would be to run each of the twelve experimental wafers, in random order, one per furnace run. That would increase the experimental error of each resistivity measurement by the run-to-run furnace variability and make it more difficult to study the effects of the different dosages. The blocked way to run this experiment, assuming you can convince manufacturing to let you put four experimental wafers in a furnace run, would be to put four wafers with different dosages in each of three furnace runs. The only randomization would be choosing which of the three wafers with dosage 1 would go into furnace run 1, and similarly for the wafers with dosages 2, 3 and 4.
Description of the experiment
Let X1 be dosage "level" and X2 be the blocking factor furnace run. Then the experiment can be described as follows:
- k = 2 factors (1 primary factor X1 and 1 blocking factor X2)
- L1 = 4 levels of factor X1
- L2 = 3 levels of factor X2
- n = 1 replication per cell
- N = L1 * L2 = 4 * 3 = 12 runs
Before randomization, the design trials look like:
| X1 | X2 |
|---|---|
| 1 | 1 |
| 1 | 2 |
| 1 | 3 |
| 2 | 1 |
| 2 | 2 |
| 2 | 3 |
| 3 | 1 |
| 3 | 2 |
| 3 | 3 |
| 4 | 1 |
| 4 | 2 |
| 4 | 3 |
Matrix representation
An alternate way of summarizing the design trials would be to use a 4x3 matrix whose 4 rows are the levels of the treatment X1 and whose columns are the 3 levels of the blocking variable X2. The cells in the matrix have indices that match the X1, X2 combinations above.
| Treatment | Block 1 | Block 2 | Block 3 |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 2 | 1 | 1 | 1 |
| 3 | 1 | 1 | 1 |
| 4 | 1 | 1 | 1 |
By extension, note that the trials for any K-factor randomized block design are simply the cell indices of a k dimensional matrix.
Model
The model for a randomized block design with one nuisance variable is
- [math]\displaystyle{ Y_{ij} = \mu + T_i + B_j + \mathrm{random\ error} }[/math]
where
- Yij is any observation for which X1 = i and X2 = j
- X1 is the primary factor
- X2 is the blocking factor
- μ is the general location parameter (i.e., the mean)
- Ti is the effect for being in treatment i (of factor X1)
- Bj is the effect for being in block j (of factor X2)
Estimates
- Estimate for μ : [math]\displaystyle{ \overline{Y} }[/math] = the average of all the data
- Estimate for Ti : [math]\displaystyle{ \overline{Y}_{i\cdot} - \overline{Y} }[/math] with [math]\displaystyle{ \overline{Y}_{i\cdot} }[/math] = average of all Y for which X1 = i.
- Estimate for Bj : [math]\displaystyle{ \overline{Y}_{\cdot j} - \overline{Y} }[/math] with [math]\displaystyle{ \overline{Y}_{\cdot j} }[/math] = average of all Y for which X2 = j.
Generalizations
- Generalized randomized block designs (GRBD) allow tests of block–treatment interaction, and has exactly one blocking factor like the RCBD.
- Latin squares (and other row–column designs) have two blocking factors that are believed to have no interaction.
- Latin hypercube sampling
- Graeco-Latin squares
- Hyper-Graeco-Latin square designs
See also
- Algebraic statistics
- Block design
- Combinatorial design
- Generalized randomized block design
- Glossary of experimental design
- Optimal design
- Paired difference test
- Dependent and independent variables
- Blockmodeling
References
- ↑ 1.0 1.1 Box, Joan Fisher (1980). "R. A. Fisher and the Design of Experiments, 1922-1926". The American Statistician 34 (1): 1–7. doi:10.2307/2682986. ISSN 0003-1305. https://www.jstor.org/stable/2682986.
- ↑ 2.0 2.1 "5.3.3.3.3. Blocking of full factorial designs". https://www.itl.nist.gov/div898/handbook/pri/section3/pri3333.htm.
- ↑ 3.0 3.1 3.2 3.3 3.4 "5.3.3.2. Randomized block designs". https://www.itl.nist.gov/div898/handbook/pri/section3/pri332.htm#:~:text=The%20general%20rule%20is:,of%20the%20remaining%20nuisance%20variables..
- ↑ 4.0 4.1 4.2 4.3 Berger, Paul D.; Maurer, Robert E.; Celli, Giovana B. (2018). "Experimental Design" (in en). SpringerLink. doi:10.1007/978-3-319-64583-4. https://link.springer.com/book/10.1007/978-3-319-64583-4.
- ↑ "Randomized Block Design" (in en), The Concise Encyclopedia of Statistics (New York, NY: Springer): pp. 447–448, 2008, doi:10.1007/978-0-387-32833-1_344, ISBN 978-0-387-32833-1, https://doi.org/10.1007/978-0-387-32833-1_344, retrieved 2023-12-11
- ↑ Bernstein S.N. (1926) Sur l'extension du théorème limite du calcul des probabilités aux sommes de quantités dépendantes. Math. Annalen, v. 97, 1–59.
- ↑ Ibragimov I.A. and Linnik Yu.V. (1971) Independent and stationary sequences of random variables. Wolters-Noordhoff, Groningen.
- ↑ Leadbetter M.R., Lindgren G. and Rootzén H. (1983) Extremes and Related Properties of Random Sequences and Processes. New York: Springer Verlag.
- ↑ Novak S.Y. (2011) Extreme Value Methods with Applications to Finance. Chapman & Hall/CRC Press, London.
- ↑ Karmakar, Biikram (November 2022). "An Approximation Algorithm for Blocking of an Experimental Design". Journal of Royal Statistical Society: 1726-1750. https://academic.oup.com/jrsssb/article/84/5/1726/7072889.
- ↑ Pashley, Nicole E.; Miratrix, Luke W. (July 7, 2021). "Block What You Can, Except When You Shouldn’t" (in en). Journal of Educational and Behavioral Statistics 47 (1): 69–100. doi:10.3102/10769986211027240. ISSN 1076-9986. http://journals.sagepub.com/doi/10.3102/10769986211027240.
- ↑ 12.0 12.1 Ledolter, Johannes; Kardon, Randy H. (2020-07-09). "Focus on Data: Statistical Design of Experiments and Sample Size Selection Using Power Analysis". Investigative Ophthalmology & Visual Science 61 (8): 11. doi:10.1167/iovs.61.8.11. ISSN 0146-0404. PMID 32645134. PMC 7425741. https://www.ncbi.nlm.nih.gov/pmc/articles/PMC7425741/.
 This article incorporates public domain material from the National Institute of Standards and Technology website https://www.nist.gov.
This article incorporates public domain material from the National Institute of Standards and Technology website https://www.nist.gov.
Bibliography
- Addelman, S. (1969). "The Generalized Randomized Block Design". The American Statistician 23 (4): 35–36. doi:10.2307/2681737.
- Addelman, S. (1970). "Variability of Treatments and Experimental Units in the Design and Analysis of Experiments". Journal of the American Statistical Association 65 (331): 1095–1108. doi:10.2307/2284277.
- Anscombe, F.J. (1948). "The Validity of Comparative Experiments". Journal of the Royal Statistical Society. A (General) 111 (3): 181–211. doi:10.2307/2984159.
- Bailey, R. A (2008). Design of Comparative Experiments. Cambridge University Press. ISBN 978-0-521-68357-9. http://www.maths.qmul.ac.uk/~rab/DOEbook/. Retrieved 2010-02-22. Pre-publication chapters are available on-line.
- Bapat, R. B. (2000). Linear Algebra and Linear Models (Second ed.). Springer. ISBN 978-0-387-98871-9. https://books.google.com/books?id=T5dsExIP3aAC.
- Caliński T.; Kageyama S. (2000). Block designs: A Randomization approach. I: Analysis. New York: Springer-Verlag. ISBN 0-387-98578-6. https://archive.org/details/blockdesignsrand0002cali.
- Caliński T.; Kageyama S. (2003). Block designs: A Randomization approach. II: Design. New York: Springer-Verlag. ISBN 0-387-95470-8. https://archive.org/details/blockdesignsrand0002cali.
- Gates, C.E. (Nov 1995). "What Really Is Experimental Error in Block Designs?". The American Statistician 49 (4): 362–363. doi:10.2307/2684574.
- Kempthorne, Oscar (1979). The Design and Analysis of Experiments (Corrected reprint of (1952) Wiley ed.). Robert E. Krieger. ISBN 0-88275-105-0.
- Hinkelmann, Klaus; Kempthorne, Oscar (2008). Design and Analysis of Experiments. I and II (Second ed.). Wiley. ISBN 978-0-470-38551-7.
- Hinkelmann, Klaus; Kempthorne, Oscar (2008). Design and Analysis of Experiments. I: Introduction to Experimental Design (Second ed.). Wiley. ISBN 978-0-471-72756-9.
- Hinkelmann, Klaus; Kempthorne, Oscar (2005). Design and Analysis of Experiments. 2: Advanced Experimental Design (First ed.). Wiley. ISBN 978-0-471-55177-5.
- Lentner, Marvin; Thomas Bishop (1993). "The Generalized RCB Design (Chapter 6.13)". Experimental design and analysis (Second ed.). Blacksburg, VA: Valley Book Company. pp. 225–226. ISBN 0-9616255-2-X.
- Raghavarao, Damaraju (1988). Constructions and Combinatorial Problems in Design of Experiments (corrected reprint of the 1971 Wiley ed.). New York: Dover. ISBN 0-486-65685-3. https://archive.org/details/constructionscom0000ragh.
- Raghavarao, Damaraju; Padgett, L.V. (2005). Block Designs: Analysis, Combinatorics and Applications. World Scientific. ISBN 981-256-360-1.
- Shah, Kirti R.; Sinha, Bikas K. (1989). Theory of Optimal Designs. Springer-Verlag. ISBN 0-387-96991-8.
- . Oxford U. P. [Clarendon]. 1987. ISBN 0-19-853256-3.
- Wilk, M. B. (1955). "The Randomization Analysis of a Generalized Randomized Block Design". Biometrika 42 (1–2): 70–79. doi:10.2307/2333423.
- Zyskind, George (1963). "Some Consequences of randomization in a Generalization of the Balanced Incomplete Block Design". The Annals of Mathematical Statistics 34 (4): 1569–1581. doi:10.1214/aoms/1177703889.
 |