Radar chart
A radar chart is a graphical method of displaying multivariate data in the form of a two-dimensional chart of three or more quantitative variables represented on axes starting from the same point. The relative position and angle of the axes is typically uninformative, but various heuristics, such as algorithms that plot data as the maximal total area, can be applied to sort the variables (axes) into relative positions that reveal distinct correlations, trade-offs, and a multitude of other comparative measures.[1]
The radar chart is also known as web chart, spider chart, spider graph, spider web chart, star chart,[2] star plot, cobweb chart, irregular polygon, polar chart, or Kiviat diagram.[3][4] It is equivalent to a parallel coordinates plot, with the axes arranged radially.
Overview
The radar chart is a chart and/or plot that consists of a sequence of equi-angular spokes, called radii, with each spoke representing one of the variables. The data length of a spoke is proportional to the magnitude of the variable for the data point relative to the maximum magnitude of the variable across all data points. A line is drawn connecting the data values for each spoke. This gives the plot a star-like appearance and the origin of one of the popular names for this plot. The star plot can be used to answer the following questions:[5]
- Which observations are most similar, i.e., are there clusters of observations? (Radar charts are used to examine the relative values for a single data point (e.g., point 3 is large for variables 2 and 4, small for variables 1, 3, 5, and 6) and to locate similar points or dissimilar points.)[5]
- Are there outliers?
Radar charts are a useful way to display multivariate observations with an arbitrary number of variables.[6] Each star represents a single observation. Typically, radar charts are generated in a multi-plot format with many stars on each page and each star representing one observation.[5] The star plot was first used by Georg von Mayr in 1877.[7][8] Radar charts differ from glyph plots in that all variables are used to construct the plotted star figure. There is no separation into foreground and background variables. Instead, the star-shaped figures are usually arranged in a rectangular array on the page. It is somewhat easier to see patterns in the data if the observations are arranged in some non-arbitrary order (if the variables are assigned to the rays of the star in some meaningful order).[9]
Applications
Radar charts can be used in sports to chart players' strengths and weaknesses[10] by calculating various statistics related to the player that can tracked along the central axis of the chart. Examples include a basketball players shots made, rebounds, assists, etc., or the batting or pitching stats of a baseball player. This creates a centralized visualization of the strengths and weaknesses of a player, and if overlapped with the statistics of other players or league averages, can display where a player excels and where they could improve.[11] These insights into player strengths and weakness could prove crucial to player development as it allows coaches and trainers to adjust a player's training regiment to help improve on their weaknesses. The results of the radar chart can also be useful in situational play. If a batter is shown to hit poorly against left-handed pitching, then his team knows to limit his plate appearances against left-handed pitchers, while the opposing team may try to force a situation where the batter is forced to hit against the pitcher.
Another application of radar charts is the control of quality improvement to display the performance metrics various objects including computer programs,[12] computers, phones, vehicles, and more. Computer programmer often use analytics to test the performance of their programs versus others. An example of this where radar charts may be useful is the performance analysis of various sorting algorithms. A programmer could gather up several different sorting algorithms such as selection, bubble, and quick, then analyze the performance of these algorithms by measuring their speed, memory usage, and power usage, then graph these on a radar chart to see how each sort performs under various sizes of data. Another performance application is measuring the performance of similar cars against each other. A consumer could look at variables such as the cars’ top speed, miles per gallon, horsepower, and torque. Then after using a radar chart to visualize the data, they could decide on what car is best for them based on the results.

Radar charts can be used in life sciences to display the strengths and weakness of drugs and other medications.[13] Using the example of two anti-depressants, a researcher can rank variables such as efficacy, side effects, cost, etc. on a scale of one to ten. They could then graph the results using a radar chart to see the spread of variables and find how the differ, such as one anti-depressant being cheaper and quicker acting, but not having great relief over time. Meanwhile, the other anti-depressant provides stronger relief and holds up better over time but is more expensive. Another life science application is in patient analysis. Radar charts can be used to graph the variables of life affecting a person's wellness, and then be analyzed to help them. A more specific example is in the case of athletes, whose various wellness habits such as sleep, diet, and stress are monitored to make sure they stay in peak physical condition.[14] If any areas would be shown dipping, doctors and trainers could step in to assist the athlete and improve their wellness.
Limitations
Radar charts are primarily suited for strikingly showing outliers and commonality, or when one chart is greater in every variable than another, and primarily used for ordinal measurements – where each variable corresponds to "better" in some respect, and all variables on the same scale.
Conversely, radar charts have been criticized as poorly suited for making trade-off decisions – when one chart is greater than another on some variables, but less on others.[15]
Further, it is hard to visually compare lengths of different spokes, because radial distances are hard to judge, though concentric circles help as grid lines. Instead, one may use a simple line graph, particularly for time series.[16]
Radar charts can distort data to some extent, especially when areas are filled in, because the area contained becomes proportional to the square of the linear measures. For example, in a chart with 5 variables that range from 1 to 100, the area contained by the polygon bounded by 5 points when all measures are 90, is more than 10% larger than the same for a chart with all values of 82.
Radar charts can also become hard to visually compare between different samples on the chart when their values are close as their lines or areas bleed into each other, as shown in Figure 5.
Artificial structure
Radar charts impose several structures on data, which are often artificial:
- Relatedness of neighbors – radar charts are often used when neighboring variables are unrelated, creating spurious connections.
- Cyclic structure – the first and last variables are placed next to each other.
- Length – variables are often most naturally ordinal: better or worse, though the degree of difference may be artificial.
- Area – area scales as the square of values, exaggerating the effect of large numbers. For example, 2, 2 takes up 4 times the area of 1, 1. This is a general issue with area graphs, and area is hard to judge – see "Cleveland's hierarchy".[17][18]
For example, the alternating data 9, 1, 9, 1, 9, 1 yields a spiking radar chart (which goes in and out), while reordering the data as 9, 9, 9, 1, 1, 1 instead yields two distinct wedges (sectors).
In some cases there is a natural structure, and radar charts can be well-suited. For example, for diagrams of data that vary over a 24-hour cycle, the hourly data is naturally related to its neighbor, and has a cyclic structure, so it can naturally be displayed as a radar chart.[16][19][20]
One set of guidelines on the use of radar charts (or rather the closely related "polar area graph") is:[20]
- you don't mind reading stacked areas instead of position along a common scale (see Cleveland's Hierarchy),
- the data set is truly cyclic, not linear, and
- there are two series to compare, one much smaller than the other
Data set size
Radar charts are helpful for small-to-moderate-sized multivariate data sets. Their primary weakness is that their effectiveness is limited to data sets with less than a few hundred points. After that, they tend to be overwhelming.[5]
Further, when using radar charts with multiple dimensions or samples, the radar chart may become cluttered and harder to interpret as the number of samples grows.
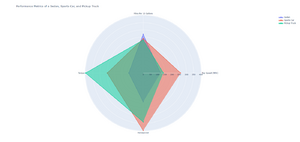
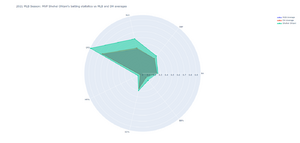
For example, take the batting stats table comparing MLB 2021 MVP Shohei Ohtani, vs the stats of the leagues average designated hitters and some Hall of Fame players. These stats represent the percentage of hits, home runs, strike outs, etc. per at bat of a player. For more information on what each stat used in the table represents, you can refer to this reference by the MLB.[21] We will use this table below to create Radar charts comparing the 2021 MVP batting stats to the league averages for Designated Hitters and regular batters, in an attempt to visualize performance metrics and visually come to a conclusion that Shohei out performed the average player. Next we will include additional samples into the Radar chart, using Hall of Fame players Jackie Robinson, Jim Thome, and Frank Thomas to compare Shohei to a few of the greatest batters of all time. This Radar chart not only can give us intuition of how Shohei compares to the top historical players, but will also serve a purpose in showing the limitations of having too many samples in a Radar chart.
| Target | BA | OBP | SLG | OPS | HR% | SO% | BB% |
|---|---|---|---|---|---|---|---|
| MLB | 0.244 | 0.317 | 0.411 | 0.728 | 0.037 | 0.232 | 0.087 |
| DH | 0.239 | 0.316 | 0.434 | 0.75 | 0.047 | 0.256 | 0.093 |
| Shohei Ohtani | 0.257 | 0.372 | 0.592 | 0.965 | 0.086 | 0.296 | 0.15 |
| Jackie Robinson | 0.313 | 0.41 | 0.477 | 0.887 | 0.0282 | 0.0582 | 0.151 |
| Jim Thome | 0.276 | 0.402 | 0.554 | 0.956 | 0.072 | 0.302 | 0.207 |
| Frank Thomas | 0.301 | 0.419 | 0.555 | 0.974 | 0.063 | 0.17 | 0.203 |
We can see in Figure 10 how a radar chart can be easily interpreted when the number of spokes and samples is relatively small. When we compare more samples in Figure 11, even without an area fill on the radar chart, it becomes apparent how difficult it can become to interpret or make trade-off decisions.
Example
The chart on the right[5] contains the star plots of 15 cars. The variable list for the sample star plot is:
- Price
- Mileage (MPG)
- 1978 Repair Record (1 = Worst, 5 = Best)
- 1977 Repair Record (1 = Worst, 5 = Best)
- Headroom
- Rear Seat Room
- Trunk Space
- Weight
- Length
We can look at these plots individually or we can use them to identify clusters of cars with similar features. For example, we can look at the star plot of the Cadillac Seville (the last one on the image) and see that it is one of the most expensive cars, gets below average (but not among the worst) gas mileage, has an average repair record, and has average-to-above-average roominess and size. We can then compare the Cadillac models (the last three plots) with the AMC models (the first three plots). This comparison shows distinct patterns. The AMC models tend to be inexpensive, have below average gas mileage, and are small in both height and weight and in roominess. The Cadillac models are expensive, have poor gas mileage, and are large in both size and roominess.[5]
Alternatives
One may use line graphs for time series and other data,[16] in the form of parallel coordinates.
For graphical qualitative comparison of 2-dimensional tabular data in several variables, a common alternative are Harvey balls, which are used extensively by Consumer Reports.[22] Comparison in Harvey balls (and radar charts) may be significantly aided by ordering the variables algorithmically to add order.[23]
An excellent way for visualising structures within multivariate data is offered by principal component analysis (PCA).
Another alternative is to use small, inline bar charts, which may be compared to sparklines.[23]
Although radar and polar charts are often described as the same chart types,[4] some sources make a difference between them and even consider the radar chart to be a polar chart's variation that does not display data in terms of polar coordinate.[24]
See also
- Plan position indicator
- Plot (graphics)
- Polar area diagram
- Parallel coordinates
- Radial tree
References
![]() This article incorporates public domain material from the National Institute of Standards and Technology website https://www.nist.gov.
This article incorporates public domain material from the National Institute of Standards and Technology website https://www.nist.gov.
- ↑ Porter, Michael M; Niksiar, Pooya (2018). "Multidimensional mechanics: Performance mapping of natural biological systems using permutated radar charts". PLOS ONE 13 (9): e0204309. doi:10.1371/journal.pone.0204309. PMID 30265707. Bibcode: 2018PLoSO..1304309P.
- ↑ Nancy R. Tague (2005) The quality toolbox. page 437.
- ↑ Kolence, Kenneth W. (1973). "The Software Empiricist". ACM SIGMETRICS Performance Evaluation Review 2 (2): 31–36. doi:10.1145/1113644.1113647. "Dr. Philip J. Kiviat suggested at a recent NBS/ACM workshop on performance measurement that a circular graph, using radii as the variable axes might be a useful form. […] I recommend they be called "Kiviat Plots" or "Kiviat Graphs" to recognize his insight as to their importance.".
- ↑ Jump up to: 4.0 4.1 "Find Content Gaps Using Radar Charts". Content Strategy Workshops. March 3, 2015. http://www.content-workshops.com/toolbox/2015/2/find-content-gaps-using-radar-charts.
- ↑ Jump up to: 5.0 5.1 5.2 5.3 5.4 5.5 NIST/SEMATECH (2003). Star Plot in: e-Handbook of Statistical Methods. 6/01/2003 (Date created)
- ↑ Chambers, John, William Cleveland, Beat Kleiner, and Paul Tukey, (1983). Graphical Methods for Data Analysis. Wadsworth. pp. 158–162
- ↑ Mayr, Georg von (1877) (in de), Die Gesetzmäßigkeit im Gesellschaftsleben, Munich: Oldenbourg, p.78. Linien-Diagramme im Kreise: Line charts in circles.
- ↑ Michael Friendly (2008). "Milestones in the history of thematic cartography, statistical graphics, and data visualization" .
- ↑ Michael Friendly (1991). "Statistical Graphics for Multivariate Data". Paper presented at the SAS SUGI 16 Conference, Apr, 1991.
- ↑ Spider Graphs: Charting Basketball Statistics
- ↑ Seeing Data. "Making sense of data visualizations" (in en-US). Seeing Data. http://seeingdata.org/taketime/inside-the-chart-radar-chart/.
- ↑ Ron Basu (2004). Implementing Quality: A Practical Guide to Tools and Techniques. p.131.
- ↑ Model Systems Knowledge Translation Center. "Effective Use of Radar Charts" (in en-US). Model Systems Knowledge Translation Center. https://msktc.org/lib/docs/KT_Toolkit/Charts_and_Graphs/Charts_and_Graphics_Radar_508c.pdf.
- ↑ John Maguire. "De-normalized Spider and Radar Graphs" (in en-US). Kitman Labs. https://www.kitmanlabs.com/.
- ↑ You are NOT spider man, so why do you use radar charts?, by Chandoo, September 18th, 2008
- ↑ Jump up to: 16.0 16.1 16.2 Peltier, Jon (2008-08-14). "Rock Around The Clock - Peltier Tech Blog". Peltiertech.com. http://peltiertech.com/WordPress/rock-around-the-clock/.
- ↑ Cleveland, William; McGill, Robert (1984). "Graphical Perception: Theory, Experimentation, and Application to the Development of Graphical Methods". Journal of the American Statistical Association 79 (387): 531–554. Summary of Cleveland's hierarchy
- ↑ (Cleveland McGill), summarized at http://processtrends.com/toc_data_visualization.htm[|permanent dead link|dead link}}]
- ↑ "Charting around the clock The Excel Charts Blog". Excelcharts.com. 2008-08-15. http://www.excelcharts.com/blog/charting-around-the-clock/.
- ↑ Jump up to: 20.0 20.1 Clock This
- ↑ "Standard Stats". https://www.mlb.com/glossary/standard-stats.
- ↑ "Qualitative Comparison". 11 December 2007. http://supportanalytics.com/blog/2007/12/qualitative-comparison/.
- ↑ Jump up to: 23.0 23.1 "Information Ocean: Reorderable tables II: Bertin versus the Spiders". I-ocean.blogspot.com. 2008-09-24. http://i-ocean.blogspot.com/2008/09/reorderable-tables-ii-bertin-versus.html.
- ↑ "Polar Charts (Report Builder and SSRS)". Microsoft Developer Network. https://msdn.microsoft.com/en-us/library/dd239337.aspx.
External links
- Star Plot – NIST/SEMATECH e-Handbook of Statistical Methods
 |