Sample size determination
Sample size determination or estimation is the act of choosing the number of observations or replicates to include in a statistical sample. The sample size is an important feature of any empirical study in which the goal is to make inferences about a population from a sample. In practice, the sample size used in a study is usually determined based on the cost, time, or convenience of collecting the data, and the need for it to offer sufficient statistical power. In complex studies, different sample sizes may be allocated, such as in stratified surveys or experimental designs with multiple treatment groups. In a census, data is sought for an entire population, hence the intended sample size is equal to the population. In experimental design, where a study may be divided into different treatment groups, there may be different sample sizes for each group.
Sample sizes may be chosen in several ways:
- using experience – small samples, though sometimes unavoidable, can result in wide confidence intervals and risk of errors in statistical hypothesis testing.
- using a target variance for an estimate to be derived from the sample eventually obtained, i.e., if a high precision is required (narrow confidence interval) this translates to a low target variance of the estimator.
- the use of a power target, i.e. the power of statistical test to be applied once the sample is collected.
- using a confidence level, i.e. the larger the required confidence level, the larger the sample size (given a constant precision requirement).
Introduction
Sample size determination is a crucial aspect of research methodology that plays a significant role in ensuring the reliability and validity of study findings. In order to influence the accuracy of estimates, the power of statistical tests, and the general robustness of the research findings, it entails carefully choosing the number of participants or data points to be included in a study.
Consider the case where we are conducting a survey to determine the average satisfaction level of customers regarding a new product. To determine an appropriate sample size, we need to consider factors such as the desired level of confidence, margin of error, and variability in the responses. We might decide that we want a 95% confidence level, meaning we are 95% confident that the true average satisfaction level falls within the calculated range. We also decide on a margin of error, of ±3%, which indicates the acceptable range of difference between our sample estimate and the true population parameter. Additionally, we may have some idea of the expected variability in satisfaction levels based on previous data or assumptions.
Importance
Larger sample sizes generally lead to increased precision when estimating unknown parameters. For instance, to accurately determine the prevalence of pathogen infection in a specific species of fish, it is preferable to examine a sample of 200 fish rather than 100 fish. Several fundamental facts of mathematical statistics describe this phenomenon, including the law of large numbers and the central limit theorem.
In some situations, the increase in precision for larger sample sizes is minimal, or even non-existent. This can result from the presence of systematic errors or strong dependence in the data, or if the data follows a heavy-tailed distribution, or because the data is strongly dependent or biased.
Sample sizes may be evaluated by the quality of the resulting estimates, as follows. It is usually determined on the basis of the cost, time or convenience of data collection and the need for sufficient statistical power. For example, if a proportion is being estimated, one may wish to have the 95% confidence interval be less than 0.06 units wide. Alternatively, sample size may be assessed based on the power of a hypothesis test. For example, if we are comparing the support for a certain political candidate among women with the support for that candidate among men, we may wish to have 80% power to detect a difference in the support levels of 0.04 units.
Estimation
Estimation of a proportion
A relatively simple situation is estimation of a proportion. It is a fundamental aspect of statistical analysis, particularly when gauging the prevalence of a specific characteristic within a population. For example, we may wish to estimate the proportion of residents in a community who are at least 65 years old.
The estimator of a proportion is , where X is the number of 'positive' instances (e.g., the number of people out of the n sampled people who are at least 65 years old). When the observations are independent, this estimator has a (scaled) binomial distribution (and is also the sample mean of data from a Bernoulli distribution). The maximum variance of this distribution is 0.25, which occurs when the true parameter is p = 0.5. In practical applications, where the true parameter p is unknown, the maximum variance is often employed for sample size assessments. If a reasonable estimate for p is known the quantity may be used in place of 0.25.
As the sample size n grows sufficiently large, the distribution of will be closely approximated by a normal distribution.[1] Using this and the Wald method for the binomial distribution, yields a confidence interval, with Z representing the standard Z-score for the desired confidence level (e.g., 1.96 for a 95% confidence interval), in the form:
To determine an appropriate sample size n for estimating proportions, the equation below can be solved, where W represents the desired width of the confidence interval. The resulting sample size formula, is often applied with a conservative estimate of p (e.g., 0.5):
for n, yielding the sample size
, in the case of using 0.5 as the most conservative estimate of the proportion. (Note: W/2 = margin of error.)
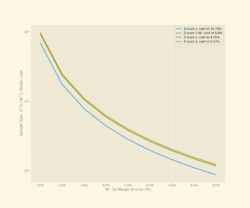
In the figure below one can observe how sample sizes for binomial proportions change given different confidence levels and margins of error.
Otherwise, the formula would be , which yields .
For example, in estimating the proportion of the U.S. population supporting a presidential candidate with a 95% confidence interval width of 2 percentage points (0.02), a sample size of (1.96)2/ (0.022) = 9604 is required with the margin of error in this case is 1 percentage point. It is reasonable to use the 0.5 estimate for p in this case because the presidential races are often close to 50/50, and it is also prudent to use a conservative estimate. The margin of error in this case is 1 percentage point (half of 0.02).
In practice, the formula : is commonly used to form a 95% confidence interval for the true proportion. The equation can be solved for n, providing a minimum sample size needed to meet the desired margin of error W. The foregoing is commonly simplified:[2][3] n = 4/W2 = 1/B2 where B is the error bound on the estimate, i.e., the estimate is usually given as within ± B. For B = 10% one requires n = 100, for B = 5% one needs n = 400, for B = 3% the requirement approximates to n = 1000, while for B = 1% a sample size of n = 10000 is required. These numbers are quoted often in news reports of opinion polls and other sample surveys. However, the results reported may not be the exact value as numbers are preferably rounded up. Knowing that the value of the n is the minimum number of sample points needed to acquire the desired result, the number of respondents then must lie on or above the minimum.
Estimation of a mean
Simply speaking, if we are trying to estimate the average time it takes for people to commute to work in a city. Instead of surveying the entire population, you can take a random sample of 100 individuals, record their commute times, and then calculate the mean (average) commute time for that sample. For example, person 1 takes 25 minutes, person 2 takes 30 minutes, ..., person 100 takes 20 minutes. Add up all the commute times and divide by the number of people in the sample (100 in this case). The result would be your estimate of the mean commute time for the entire population. This method is practical when it's not feasible to measure everyone in the population, and it provides a reasonable approximation based on a representative sample.
In a precisely mathematical way, when estimating the population mean using an independent and identically distributed (iid) sample of size n, where each data value has variance σ2, the standard error of the sample mean is:
This expression describes quantitatively how the estimate becomes more precise as the sample size increases. Using the central limit theorem to justify approximating the sample mean with a normal distribution yields a confidence interval of the form
- ,
- where Z is a standard Z-score for the desired level of confidence (1.96 for a 95% confidence interval).
To determine the sample size n required for a confidence interval of width W, with W/2 as the margin of error on each side of the sample mean, the equation
- can be solved. This yields the sample size formula, for n:
.
For instance, if estimating the effect of a drug on blood pressure with a 95% confidence interval that is six units wide, and the known standard deviation of blood pressure in the population is 15, the required sample size would be , which would be rounded up to 97, since sample sizes must be integers and must meet or exceed the calculated minimum value. Understanding these calculations is essential for researchers designing studies to accurately estimate population means within a desired level of confidence.
Required sample sizes for hypothesis tests
One of the prevalent challenges faced by statisticians revolves around the task of calculating the sample size needed to attain a specified statistical power for a test, all while maintaining a pre-determined Type I error rate α, which signifies the level of significance in hypothesis testing. It yields a certain power for a test, given a predetermined. As follows, this can be estimated by pre-determined tables for certain values, by formulas, by simulation, by Mead's resource equation, or by the cumulative distribution function:
Tables
| [4] Power |
Cohen's d | ||
|---|---|---|---|
| 0.2 | 0.5 | 0.8 | |
| 0.25 | 84 | 14 | 6 |
| 0.50 | 193 | 32 | 13 |
| 0.60 | 246 | 40 | 16 |
| 0.70 | 310 | 50 | 20 |
| 0.80 | 393 | 64 | 26 |
| 0.90 | 526 | 85 | 34 |
| 0.95 | 651 | 105 | 42 |
| 0.99 | 920 | 148 | 58 |
The table shown on the right can be used in a two-sample t-test to estimate the sample sizes of an experimental group and a control group that are of equal size, that is, the total number of individuals in the trial is twice that of the number given, and the desired significance level is 0.05.[4] The parameters used are:
- The desired statistical power of the trial, shown in column to the left.
- Cohen's d (= effect size), which is the expected difference between the means of the target values between the experimental group and the control group, divided by the expected standard deviation.
Formulas
Calculating a required sample size is often not easy since the distribution of the test statistic under the alternative hypothesis of interest is usually hard to work with. Approximate sample size formulas for specific problems are available - some general references are [5] and [6]
A computational approach (QuickSize)
The QuickSize algorithm [7] is a very general approach that is simple to use yet versatile enough to give an exact solution for a broad range of problems. It uses simulation together with a search algorithm.
Mead's resource equation
Mead's resource equation is often used for estimating sample sizes of laboratory animals, as well as in many other laboratory experiments. It may not be as accurate as using other methods in estimating sample size, but gives a hint of what is the appropriate sample size where parameters such as expected standard deviations or expected differences in values between groups are unknown or very hard to estimate.[8]
All the parameters in the equation are in fact the degrees of freedom of the number of their concepts, and hence, their numbers are subtracted by 1 before insertion into the equation.
The equation is:[8]
where:
- N is the total number of individuals or units in the study (minus 1)
- B is the blocking component, representing environmental effects allowed for in the design (minus 1)
- T is the treatment component, corresponding to the number of treatment groups (including control group) being used, or the number of questions being asked (minus 1)
- E is the degrees of freedom of the error component and should be somewhere between 10 and 20.
For example, if a study using laboratory animals is planned with four treatment groups (T=3), with eight animals per group, making 32 animals total (N=31), without any further stratification (B=0), then E would equal 28, which is above the cutoff of 20, indicating that sample size may be a bit too large, and six animals per group might be more appropriate.[9]
Cumulative distribution function
Let Xi, i = 1, 2, ..., n be independent observations taken from a normal distribution with unknown mean μ and known variance σ2. Consider two hypotheses, a null hypothesis:
and an alternative hypothesis:
for some 'smallest significant difference' μ* > 0. This is the smallest value for which we care about observing a difference. Now, for (1) to reject H0 with a probability of at least 1 − β when Ha is true (i.e. a power of 1 − β), and (2) reject H0 with probability α when H0 is true, the following is necessary: If zα is the upper α percentage point of the standard normal distribution, then
and so
- 'Reject H0 if our sample average () is more than '
is a decision rule which satisfies (2). (This is a 1-tailed test.) In such a scenario, achieving this with a probability of at least 1−β when the alternative hypothesis Ha is true becomes imperative. Here, the sample average originates from a Normal distribution with a mean of μ*. Thus, the requirement is expressed as:
Through careful manipulation, this can be shown (see Statistical power Example) to happen when
where is the normal cumulative distribution function.
Stratified sample size
With more complicated sampling techniques, such as stratified sampling, the sample can often be split up into sub-samples. Typically, if there are H such sub-samples (from H different strata) then each of them will have a sample size nh, h = 1, 2, ..., H. These nh must conform to the rule that n1 + n2 + ... + nH = n (i.e., that the total sample size is given by the sum of the sub-sample sizes). Selecting these nh optimally can be done in various ways, using (for example) Neyman's optimal allocation.
There are many reasons to use stratified sampling:[10] to decrease variances of sample estimates, to use partly non-random methods, or to study strata individually. A useful, partly non-random method would be to sample individuals where easily accessible, but, where not, sample clusters to save travel costs.[11]
In general, for H strata, a weighted sample mean is
with
The weights, , frequently, but not always, represent the proportions of the population elements in the strata, and . For a fixed sample size, that is ,
which can be made a minimum if the sampling rate within each stratum is made proportional to the standard deviation within each stratum: , where and is a constant such that .
An "optimum allocation" is reached when the sampling rates within the strata are made directly proportional to the standard deviations within the strata and inversely proportional to the square root of the sampling cost per element within the strata, :
where is a constant such that , or, more generally, when
Qualitative research
Qualitative research approaches sample size determination with a distinctive methodology that diverges from quantitative methods. Rather than relying on predetermined formulas or statistical calculations, it involves a subjective and iterative judgment throughout the research process. In qualitative studies, researchers often adopt a subjective stance, making determinations as the study unfolds. Sample size determination in qualitative studies takes a different approach. It is generally a subjective judgment, taken as the research proceeds.[16] One common approach is to continually include additional participants or materials until a point of "saturation" is reached. Saturation occurs when new participants or data cease to provide fresh insights, indicating that the study has adequately captured the diversity of perspectives or experiences within the chosen sample saturation is reached.[17] The number needed to reach saturation has been investigated empirically.[18][19][20][21]
Unlike quantitative research, qualitative studies face a scarcity of reliable guidance regarding sample size estimation prior to beginning the research. Imagine conducting in-depth interviews with cancer survivors, qualitative researchers may use data saturation to determine the appropriate sample size. If, over a number of interviews, no fresh themes or insights show up, saturation has been reached and more interviews might not add much to our knowledge of the survivor's experience. Thus, rather than following a preset statistical formula, the concept of attaining saturation serves as a dynamic guide for determining sample size in qualitative research. There is a paucity of reliable guidance on estimating sample sizes before starting the research, with a range of suggestions given.[19][22][23][24] In an effort to introduce some structure to the sample size determination process in qualitative research, a tool analogous to quantitative power calculations has been proposed. This tool, based on the negative binomial distribution, is particularly tailored for thematic analysis.[25][24]
See also
- Design of experiments
- Engineering response surface example under Stepwise regression
- Cohen's h
- Receiver operating characteristic
References
- ↑ NIST/SEMATECH, "7.2.4.2. Sample sizes required", e-Handbook of Statistical Methods.
- ↑ "Inference for Regression". utdallas.edu. http://www.utdallas.edu/~ammann/stat3355/node25.html.
- ↑ "Confidence Interval for a Proportion"
- ↑ 4.0 4.1 Chapter 13, page 215, in: Kenny, David A. (1987). Statistics for the social and behavioral sciences. Boston: Little, Brown. ISBN 978-0-316-48915-7.
- ↑ Cohen, J. (1987), Statistical Power Analysis, 2nd edition, Hillsdale(NJ):Lawrence Erlbaum Associates, Inc.
- ↑ Desu, M.M. and Raghavarao, D. (1990), Sample Size Methodology, New York:Academic Press.
- ↑ Amaratunga, D. (1999). Searching for the right sample size. The American Statistician, 53(1), 52–55. https://doi.org/10.2307/2685652
- ↑ 8.0 8.1 Kirkwood, James; Robert Hubrecht (2010). The UFAW Handbook on the Care and Management of Laboratory and Other Research Animals. Wiley-Blackwell. p. 29. ISBN 978-1-4051-7523-4. online Page 29
- ↑ Isogenic.info > Resource equation by Michael FW Festing. Updated Sept. 2006
- ↑ Kish (1965, Section 3.1)
- ↑ Kish (1965), p. 148.
- ↑ Kish (1965), p. 78.
- ↑ Kish (1965), p. 81.
- ↑ Kish (1965), p. 93.
- ↑ Kish (1965), p. 94.
- ↑ Sandelowski, M. (1995). Sample size in qualitative research. Research in Nursing & Health, 18, 179–183
- ↑ Glaser, B. (1965). The constant comparative method of qualitative analysis. Social Problems, 12, 436–445
- ↑ Francis, Jill J.; Johnston, Marie; Robertson, Clare; Glidewell, Liz; Entwistle, Vikki; Eccles, Martin P.; Grimshaw, Jeremy M. (2010). "What is an adequate sample size? Operationalising data saturation for theory-based interview studies". Psychology & Health 25 (10): 1229–1245. doi:10.1080/08870440903194015. PMID 20204937. https://openaccess.city.ac.uk/id/eprint/1732/1/What%20is%20an%20adequate%20sample%20size.pdf.
- ↑ 19.0 19.1 Guest, Greg; Bunce, Arwen; Johnson, Laura (2006). "How Many Interviews Are Enough?". Field Methods 18: 59–82. doi:10.1177/1525822X05279903.
- ↑ Wright, Adam; Maloney, Francine L.; Feblowitz, Joshua C. (2011). "Clinician attitudes toward and use of electronic problem lists: A thematic analysis". BMC Medical Informatics and Decision Making 11: 36. doi:10.1186/1472-6947-11-36. PMID 21612639.
- ↑ Mason, Mark (2010). "Sample Size and Saturation in PhD Studies Using Qualitative Interviews". Forum Qualitative Sozialforschung 11 (3): 8. http://www.qualitative-research.net/index.php/fqs/article/view/1428/3027.
- ↑ Emmel, N. (2013). Sampling and choosing cases in qualitative research: A realist approach. London: Sage.
- ↑ Onwuegbuzie, Anthony J.; Leech, Nancy L. (2007). "A Call for Qualitative Power Analyses". Quality & Quantity 41: 105–121. doi:10.1007/s11135-005-1098-1.
- ↑ 24.0 24.1 Fugard AJB; Potts HWW (10 February 2015). "Supporting thinking on sample sizes for thematic analyses: A quantitative tool". International Journal of Social Research Methodology 18 (6): 669–684. doi:10.1080/13645579.2015.1005453. http://discovery.ucl.ac.uk/1498831/3/Potts_10-7-2015_Supporting.pdf.
- ↑ Galvin R (2015). How many interviews are enough? Do qualitative interviews in building energy consumption research produce reliable knowledge? Journal of Building Engineering, 1:2–12.
General references
- Bartlett, J. E. II; Kotrlik, J. W.; Higgins, C. (2001). "Organizational research: Determining appropriate sample size for survey research". Information Technology, Learning, and Performance Journal 19 (1): 43–50. http://www.osra.org/itlpj/bartlettkotrlikhiggins.pdf. Retrieved 2009-09-07.
- Kish, L. (1965). Survey Sampling. Wiley. ISBN 978-0-471-48900-9. https://archive.org/details/surveysampling00lesl.
- Smith, Scott (8 April 2013). "Determining Sample Size: How to Ensure You Get the Correct Sample Size". https://www.qualtrics.com/experience-management/research/determine-sample-size/.
- Israel, Glenn D. (1992). "Determining Sample Size". University of Florida, PEOD-6. https://www.academia.edu/21353552. Retrieved 29 June 2019.
- Rens van de Schoot, Milica Miočević (eds.). 2020. Small Sample Size Solutions (Open Access): A Guide for Applied Researchers and Practitioners. Routledge.
Further reading
- NIST: Selecting Sample Sizes
- ASTM E122-07: Standard Practice for Calculating Sample Size to Estimate, With Specified Precision, the Average for a Characteristic of a Lot or Process
External links
- A MATLAB script implementing Cochran's sample size formula
- Sample Size Calculator for various statistical tests
- Statulator for various statistical tests
de:Zufallsstichprobe#Stichprobenumfang
 |
