Box plot

In descriptive statistics, a box plot or boxplot is a method for graphically demonstrating the locality, spread and skewness groups of numerical data through their quartiles.[1] In addition to the box on a box plot, there can be lines (which are called whiskers) extending from the box indicating variability outside the upper and lower quartiles, thus, the plot is also called the box-and-whisker plot and the box-and-whisker diagram. Outliers that differ significantly from the rest of the dataset[2] may be plotted as individual points beyond the whiskers on the box-plot. Box plots are non-parametric: they display variation in samples of a statistical population without making any assumptions of the underlying statistical distribution[3] (though Tukey's boxplot assumes symmetry for the whiskers and normality for their length). The spacings in each subsection of the box-plot indicate the degree of dispersion (spread) and skewness of the data, which are usually described using the five-number summary. In addition, the box-plot allows one to visually estimate various L-estimators, notably the interquartile range, midhinge, range, mid-range, and trimean. Box plots can be drawn either horizontally or vertically.
History
The range-bar method was first introduced by Mary Eleanor Spear in her book "Charting Statistics" in 1952[4] and again in her book "Practical Charting Techniques" in 1969.[5] The box-and-whisker plot was first introduced in 1970 by John Tukey, who later published on the subject in his book "Exploratory Data Analysis" in 1977.[6]
Elements

A boxplot is a standardized way of displaying the dataset based on the five-number summary: the minimum, the maximum, the sample median, and the first and third quartiles.
- Minimum (Q0 or 0th percentile): the lowest data point in the data set excluding any outliers
- Maximum (Q4 or 100th percentile): the highest data point in the data set excluding any outliers
- Median (Q2 or 50th percentile): the middle value in the data set
- First quartile (Q1 or 25th percentile): also known as the lower quartile qn(0.25), it is the median of the lower half of the dataset.
- Third quartile (Q3 or 75th percentile): also known as the upper quartile qn(0.75), it is the median of the upper half of the dataset.[7]
In addition to the minimum and maximum values used to construct a box-plot, another important element that can also be employed to obtain a box-plot is the interquartile range (IQR), as denoted below:
- Interquartile range (IQR) : the distance between the upper and lower quartiles
A box-plot usually includes two parts, a box and a set of whiskers as shown in Figure 2.
Box
The box is drawn from Q1 to Q3 with a horizontal line drawn inside it to denote the median. Some box plots include an additional character to represent the mean of the data.[8][9]
Whiskers
The whiskers must end at an observed data point, but can be defined in various ways. In the most straight-forward method, the boundary of the lower whisker is the minimum value of the data set, and the boundary of the upper whisker is the maximum value of the data set. Because of this variability, it is appropriate to describe the convention that is being used for the whiskers and outliers in the caption of the box-plot.
Another popular choice for the boundaries of the whiskers is based on the 1.5 IQR value. From above the upper quartile (Q3), a distance of 1.5 times the IQR is measured out and a whisker is drawn up to the largest observed data point from the dataset that falls within this distance. Similarly, a distance of 1.5 times the IQR is measured out below the lower quartile (Q1) and a whisker is drawn down to the lowest observed data point from the dataset that falls within this distance. Because the whiskers must end at an observed data point, the whisker lengths can look unequal, even though 1.5 IQR is the same for both sides. All other observed data points outside the boundary of the whiskers are plotted as outliers.[10] The outliers can be plotted on the box-plot as a dot, a small circle, a star, etc. (see example below).
There are other representations in which the whiskers can stand for several other things, such as:
- One standard deviation above and below the mean of the data set
- The 9th percentile and the 91st percentile of the data set
- The 2nd percentile and the 98th percentile of the data set
Rarely, box-plot can be plotted without the whiskers. This can be appropriate for sensitive information to avoid whiskers (and outliers) disclosing actual values observed.[11]
The unusual percentiles 2%, 9%, 91%, 98% are sometimes used for whisker cross-hatches and whisker ends to depict the seven-number summary. If the data are normally distributed, the locations of the seven marks on the box plot will be equally spaced. On some box plots, a cross-hatch is placed before the end of each whisker.
Variations

Since the mathematician John W. Tukey first popularized this type of visual data display in 1969, several variations on the classical box plot have been developed, and the two most commonly found variations are the variable width box plots and the notched box plots shown in Figure 4.
Variable width box plots illustrate the size of each group whose data is being plotted by making the width of the box proportional to the size of the group. A popular convention is to make the box width proportional to the square root of the size of the group.[12]
Notched box plots apply a "notch" or narrowing of the box around the median. Notches are useful in offering a rough guide of the significance of the difference of medians; if the notches of two boxes do not overlap, this will provide evidence of a statistically significant difference between the medians.[12] The height of the notches is proportional to the interquartile range (IQR) of the sample and is inversely proportional to the square root of the size of the sample. However, there is a uncertainty about the most appropriate multiplier (as this may vary depending on the similarity of the variances of the samples).[12] The width of the notch is arbitrarily chosen to be visually pleasing, and should be consistent amongst all box plots being displayed on the same page.
One convention for obtaining the boundaries of these notches is to use a distance of around the median.[13]
Adjusted box plots are intended to describe skew distributions, and they rely on the medcouple statistic of skewness.[14] For a medcouple value of MC, the lengths of the upper and lower whiskers on the box-plot are respectively defined to be:
For a symmetrical data distribution, the medcouple will be zero, and this reduces the adjusted box-plot to the Tukey's box-plot with equal whisker lengths of for both whiskers.
Other kinds of box plots, such as the violin plots and the bean plots can show the difference between single-modal and multimodal distributions, which cannot be observed from the original classical box-plot.[6]
Examples
Example without outliers
A series of hourly temperatures were measured throughout the day in degrees Fahrenheit. The recorded values are listed in order as follows (°F): 57, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 81.
A box plot of the data set can be generated by first calculating five relevant values of this data set: minimum, maximum, median (Q2), first quartile (Q1), and third quartile (Q3).
The minimum is the smallest number of the data set. In this case, the minimum recorded day temperature is 57 °F.
The maximum is the largest number of the data set. In this case, the maximum recorded day temperature is 81 °F.
The median is the "middle" number of the ordered data set. This means that there are exactly 50% of the elements is less than the median and 50% of the elements is greater than the median. The median of this ordered data set is 70 °F.
The first quartile value (Q1 or 25th percentile) is the number that marks one quarter of the ordered data set. In other words, there are exactly 25% of the elements that are less than the first quartile and exactly 75% of the elements that are greater than it. The first quartile value can be easily determined by finding the "middle" number between the minimum and the median. For the hourly temperatures, the "middle" number found between 57 °F and 70 °F is 66 °F.
The third quartile value (Q3 or 75th percentile) is the number that marks three quarters of the ordered data set. In other words, there are exactly 75% of the elements that are less than the third quartile and 25% of the elements that are greater than it. The third quartile value can be easily obtained by finding the "middle" number between the median and the maximum. For the hourly temperatures, the "middle" number between 70 °F and 81 °F is 75 °F.
The interquartile range, or IQR, can be calculated by subtracting the first quartile value (Q1) from the third quartile value (Q3):
Hence,
1.5 IQR above the third quartile is:
1.5 IQR below the first quartile is:
The upper whisker boundary of the box-plot is the largest data value that is within 1.5 IQR above the third quartile. Here, 1.5 IQR above the third quartile is 88.5 °F and the maximum is 81 °F. Therefore, the upper whisker is drawn at the value of the maximum, which is 81 °F.
Similarly, the lower whisker boundary of the box plot is the smallest data value that is within 1.5 IQR below the first quartile. Here, 1.5 IQR below the first quartile is 52.5 °F and the minimum is 57 °F. Therefore, the lower whisker is drawn at the value of the minimum, which is 57 °F.
Example with outliers
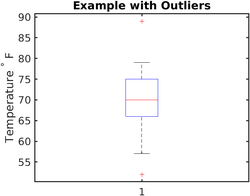
Above is an example without outliers. Here is a followup example for generating box-plot with outliers:
The ordered set for the recorded temperatures is (°F): 52, 57, 57, 58, 63, 66, 66, 67, 67, 68, 69, 70, 70, 70, 70, 72, 73, 75, 75, 76, 76, 78, 79, 89.
In this example, only the first and the last number are changed. The median, third quartile, and first quartile remain the same.
In this case, the maximum value in this data set is 89 °F, and 1.5 IQR above the third quartile is 88.5 °F. The maximum is greater than 1.5 IQR plus the third quartile, so the maximum is an outlier. Therefore, the upper whisker is drawn at the greatest value smaller than 1.5 IQR above the third quartile, which is 79 °F.
Similarly, the minimum value in this data set is 52 °F, and 1.5 IQR below the first quartile is 52.5 °F. The minimum is smaller than 1.5 IQR minus the first quartile, so the minimum is also an outlier. Therefore, the lower whisker is drawn at the smallest value greater than 1.5 IQR below the first quartile, which is 57 °F.
In the case of large datasets
An additional example for obtaining box-plot from a data set containing a large number of data points is:
General equation to compute empirical quantiles
- Here stands for the general ordering of the data points (i.e. if , then )
Using the above example that has 24 data points (n = 24), one can calculate the median, first and third quartile either mathematically or visually.
Median :
First quartile :
Third quartile :
Visualization
Although box plots may seem more primitive than histograms or kernel density estimates, they do have a number of advantages. First, the box plot enables statisticians to do a quick graphical examination on one or more data sets. Box-plots also take up less space and are therefore particularly useful for comparing distributions between several groups or sets of data in parallel (see Figure 1 for an example). Lastly, the overall structure of histograms and kernel density estimate can be strongly influenced by the choice of number and width of bins techniques and the choice of bandwidth, respectively.
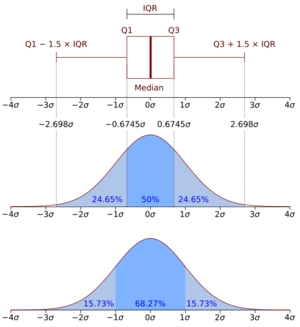
Although looking at a statistical distribution is more common than looking at a box plot, it can be useful to compare the box plot against the probability density function (theoretical histogram) for a normal N(0,σ2) distribution and observe their characteristics directly (as shown in Figure 7).

See also
- Bagplot
- Contour boxplot
- Candlestick chart
- Data and information visualization
- Exploratory data analysis
- Fan chart
- Five-number summary
- Functional boxplot
- Seven-number summary
- Sina plot
- Violin plot
References
- ↑ C., Dutoit, S. H. (2012). Graphical exploratory data analysis.. Springer. ISBN 978-1-4612-9371-2. OCLC 1019645745. http://worldcat.org/oclc/1019645745.
- ↑ Grubbs, Frank E. (February 1969). "Procedures for Detecting Outlying Observations in Samples". Technometrics 11 (1): 1–21. doi:10.1080/00401706.1969.10490657. ISSN 0040-1706. http://dx.doi.org/10.1080/00401706.1969.10490657.
- ↑ Richard., Boddy (2009). Statistical Methods in Practice : for Scientists and Technologists.. John Wiley & Sons. ISBN 978-0-470-74664-6. OCLC 940679163. http://worldcat.org/oclc/940679163.
- ↑ Spear, Mary Eleanor (1952). Charting Statistics. McGraw Hill. pp. 166.
- ↑ Spear, Mary Eleanor. (1969). Practical charting techniques. New York: McGraw-Hill. ISBN 0070600104. OCLC 924909765.
- ↑ 6.0 6.1 Wickham, Hadley; Stryjewski, Lisa. "40 years of boxplots". https://vita.had.co.nz/papers/boxplots.pdf.
- ↑ Holmes, Alexander; Illowsky, Barbara; Dean, Susan (31 March 2015). Introductory Business Statistics. https://opentextbc.ca/introbusinessstatopenstax/chapter/measures-of-the-location-of-the-data/. Retrieved 29 April 2020.
- ↑ Frigge, Michael; Hoaglin, David C.; Iglewicz, Boris (February 1989). "Some Implementations of the Boxplot". The American Statistician 43 (1): 50–54. doi:10.2307/2685173.
- ↑ Marmolejo-Ramos, F.; Tian, S. (2010). "The shifting boxplot. A boxplot based on essential summary statistics around the mean". International Journal of Psychological Research 3 (1): 37–46. doi:10.21500/20112084.823.
- ↑ Dekking, F.M. (2005). A Modern Introduction to Probability and Statistics. Springer. pp. 234–238. ISBN 1-85233-896-2. https://archive.org/details/modernintroducti00dekk_722.
- ↑ Derrick, Ben; Green, Elizabeth; Ritchie, Felix; White, Paul (September 2022). "The Risk of Disclosure When Reporting Commonly Used Univariate Statistics". Privacy in Statistical Databases 13463: 119–129. doi:10.1007/978-3-031-13945-1_9.
- ↑ 12.0 12.1 12.2 McGill, Robert; Tukey, John W.; Larsen, Wayne A. (February 1978). "Variations of Box Plots". The American Statistician 32 (1): 12–16. doi:10.2307/2683468.
- ↑ "R: Box Plot Statistics". R manual. http://stat.ethz.ch/R-manual/R-devel/library/grDevices/html/boxplot.stats.html.
- ↑ "An adjusted boxplot for skewed distribution". Computational Statistics and Data Analysis 52 (12): 5186–5201. 2008. doi:10.1016/j.csda.2007.11.008.
Further reading
- Tukey, John W. (1977). Exploratory Data Analysis. Addison-Wesley. ISBN 9780201076165. https://archive.org/details/exploratorydataa00tuke_0.
- Benjamini, Y. (1988). "Opening the Box of a Boxplot". The American Statistician 42 (4): 257–262. doi:10.2307/2685133.
- Rousseeuw, P. J.; Ruts, I.; Tukey, J. W. (1999). "The Bagplot: A Bivariate Boxplot". The American Statistician 53 (4): 382–387. doi:10.2307/2686061.
External links
- Beeswarm Boxplot - superimposing a frequency-jittered stripchart on top of a box plot
 |
