Kaplan–Meier estimator
The Kaplan–Meier estimator,[1][2] also known as the product limit estimator, is a non-parametric statistic used to estimate the survival function from lifetime data. In medical research, it is often used to measure the fraction of patients living for a certain amount of time after treatment. In other fields, Kaplan–Meier estimators may be used to measure the length of time people remain unemployed after a job loss,[3] the time-to-failure of machine parts, or how long fleshy fruits remain on plants before they are removed by frugivores. The estimator is named after Edward L. Kaplan and Paul Meier, who each submitted similar manuscripts to the Journal of the American Statistical Association.[4] The journal editor, John Tukey, convinced them to combine their work into one paper, which has been cited more than 61,800 times since its publication in 1958.[5][6]
The estimator of the survival function [math]\displaystyle{ S(t) }[/math] (the probability that life is longer than [math]\displaystyle{ t }[/math]) is given by:
- [math]\displaystyle{ \widehat S(t) = \prod\limits_{i:\ t_i\le t} \left(1 - \frac{d_i}{n_i}\right), }[/math]
with [math]\displaystyle{ t_i }[/math] a time when at least one event happened, di the number of events (e.g., deaths) that happened at time [math]\displaystyle{ t_i }[/math], and [math]\displaystyle{ n_i }[/math] the individuals known to have survived (have not yet had an event or been censored) up to time [math]\displaystyle{ t_i }[/math].
Basic concepts
A plot of the Kaplan–Meier estimator is a series of declining horizontal steps which, with a large enough sample size, approaches the true survival function for that population. The value of the survival function between successive distinct sampled observations ("clicks") is assumed to be constant.
An important advantage of the Kaplan–Meier curve is that the method can take into account some types of censored data, particularly right-censoring, which occurs if a patient withdraws from a study, is lost to follow-up, or is alive without event occurrence at last follow-up. On the plot, small vertical tick-marks state individual patients whose survival times have been right-censored. When no truncation or censoring occurs, the Kaplan–Meier curve is the complement of the empirical distribution function.
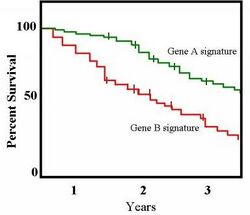
In medical statistics, a typical application might involve grouping patients into categories, for instance, those with Gene A profile and those with Gene B profile. In the graph, patients with Gene B die much quicker than those with Gene A. After two years, about 80% of the Gene A patients survive, but less than half of patients with Gene B.
To generate a Kaplan–Meier estimator, at least two pieces of data are required for each patient (or each subject): the status at last observation (event occurrence or right-censored), and the time to event (or time to censoring). If the survival functions between two or more groups are to be compared, then a third piece of data is required: the group assignment of each subject.[7]
Problem definition
Let [math]\displaystyle{ \tau\ge 0 }[/math] be a random variable, which we think of as the time that elapses between the start of the possible exposure period, [math]\displaystyle{ t_0 }[/math], and the time that an event of interest takes place, [math]\displaystyle{ t_1 }[/math]. As indicated above, the goal is to estimate the survival function [math]\displaystyle{ S }[/math] underlying [math]\displaystyle{ \tau }[/math]. Recall that this function is defined as
- [math]\displaystyle{ S(t) = \operatorname{Prob}(\tau \gt t ) }[/math], where [math]\displaystyle{ t=0,1,\dots }[/math] is the time.
Let [math]\displaystyle{ \tau_1,\dots,\tau_n\ge 0 }[/math] be independent, identically distributed random variables, whose common distribution is that of [math]\displaystyle{ \tau }[/math]: [math]\displaystyle{ \tau_j }[/math] is the random time when some event [math]\displaystyle{ j }[/math] happened. The data available for estimating [math]\displaystyle{ S }[/math] is not [math]\displaystyle{ (\tau_j)_{j=1,\dots,n} }[/math], but the list of pairs [math]\displaystyle{ (\, ( \tilde \tau_j, c_j )\, )_{j=1,\dots,n} }[/math] where for [math]\displaystyle{ j\in [n] := \{1,2,\dots,n\} }[/math], [math]\displaystyle{ c_j\ge 0 }[/math] is a fixed, deterministic integer, the censoring time of event [math]\displaystyle{ j }[/math] and [math]\displaystyle{ \tilde \tau_j = \min(\tau_j,c_j) }[/math]. In particular, the information available about the timing of event [math]\displaystyle{ j }[/math] is whether the event happened before the fixed time [math]\displaystyle{ c_j }[/math] and if so, then the actual time of the event is also available. The challenge is to estimate [math]\displaystyle{ S(t) }[/math] given this data.
Derivation of the Kaplan–Meier estimator
Here, we show two derivations of the Kaplan–Meier estimator. Both are based on rewriting the survival function in terms of what is sometimes called hazard, or mortality rates. However, before doing this it is worthwhile to consider a naive estimator.
A naive estimator
To understand the power of the Kaplan–Meier estimator, it is worthwhile to first describe a naive estimator of the survival function.
Fix [math]\displaystyle{ k\in [n]:=\{1,\dots,n\} }[/math] and let [math]\displaystyle{ t\gt 0 }[/math]. A basic argument shows that the following proposition holds:
- Proposition 1: If the censoring time [math]\displaystyle{ c_k }[/math] of event [math]\displaystyle{ k }[/math] exceeds [math]\displaystyle{ t }[/math] ([math]\displaystyle{ c_k\ge t }[/math]), then [math]\displaystyle{ \tilde \tau_k\ge t }[/math] if and only if [math]\displaystyle{ \tau_k\ge t }[/math].
Let [math]\displaystyle{ k }[/math] be such that [math]\displaystyle{ c_k\ge t }[/math]. It follows from the above proposition that
- [math]\displaystyle{ \operatorname{Prob}(\tau_k\ge t) = \operatorname{Prob}(\tilde \tau_k\ge t). }[/math]
Let [math]\displaystyle{ X_k = \mathbb{I}(\tilde \tau_k\ge t) }[/math] and consider only those [math]\displaystyle{ k\in C(t) := \{ 1\le k \le n \,:\, c_k \ge t\} }[/math], i.e. the events for which the outcome was not censored before time [math]\displaystyle{ t }[/math]. Let [math]\displaystyle{ m(t)=|C(t)| }[/math] be the number of elements in [math]\displaystyle{ C(t) }[/math]. Note that the set [math]\displaystyle{ C(t) }[/math] is not random and so neither is [math]\displaystyle{ m(t) }[/math]. Furthermore, [math]\displaystyle{ (X_k)_{k\in C(t)} }[/math] is a sequence of independent, identically distributed Bernoulli random variables with common parameter [math]\displaystyle{ S(t)=\operatorname{Prob}(\tau\ge t) }[/math]. Assuming that [math]\displaystyle{ m(t)\gt 0 }[/math], this suggests to estimate [math]\displaystyle{ S(t) }[/math] using
- [math]\displaystyle{ \hat S_\text{naive}(t) = \frac{1}{m(t)} \sum_{k:c_k\ge t} X_k = \frac{|\{1\le k \le n\,:\, \tilde \tau_k\ge t\}|}{|\{1\le k \le n\,:\, c_k\ge t\}|} = \frac{|\{1\le k \le n\,:\, \tilde \tau_k\ge t\}|}{m(t)}, }[/math]
where the second equality follows because [math]\displaystyle{ \tilde \tau_k\ge t }[/math] implies [math]\displaystyle{ c_k\ge t }[/math], while the last equality is simply a change of notation.
The quality of this estimate is governed by the size of [math]\displaystyle{ m(t) }[/math]. This can be problematic when [math]\displaystyle{ m(t) }[/math] is small, which happens, by definition, when a lot of the events are censored. A particularly unpleasant property of this estimator, that suggests that perhaps it is not the "best" estimator, is that it ignores all the observations whose censoring time precedes [math]\displaystyle{ t }[/math]. Intuitively, these observations still contain information about [math]\displaystyle{ S(t) }[/math]: For example, when for many events with [math]\displaystyle{ c_k \lt t }[/math], [math]\displaystyle{ \tilde \tau_k\lt c_k }[/math] also holds, we can infer that events often happen early, which implies that [math]\displaystyle{ \operatorname{Prob}(\tau\le t) }[/math] is large, which, through [math]\displaystyle{ S(t) = 1-\operatorname{Prob}(\tau\le t) }[/math] means that [math]\displaystyle{ S(t) }[/math] must be small. However, this information is ignored by this naive estimator. The question is then whether there exists an estimator that makes a better use of all the data. This is what the Kaplan–Meier estimator accomplishes. Note that the naive estimator cannot be improved when censoring does not take place; so whether an improvement is possible critically hinges upon whether censoring is in place.
The plug-in approach
By elementary calculations,
- [math]\displaystyle{ \begin{align} S(t) & = \operatorname{Prob}(\tau \gt t\mid\tau \gt t-1)\operatorname{Prob}(\tau \gt t-1) \\[4pt] & = (1-\operatorname{Prob}(\tau\le t\mid\tau \gt t-1)) \operatorname{Prob}(\tau \gt t-1)\\[4pt] & = (1-\operatorname{Prob}(\tau=t\mid\tau \ge t)) \operatorname{Prob}(\tau \gt t-1) \\[4pt] & = q(t) S(t-1)\,, \end{align} }[/math]
where the second to last equality used that [math]\displaystyle{ \tau }[/math] is integer valued and for the last line we introduced
- [math]\displaystyle{ q(t) = 1-\operatorname{Prob}(\tau=t\mid\tau\ge t). }[/math]
By a recursive expansion of the equality [math]\displaystyle{ S(t) = q(t) S(t-1) }[/math], we get
- [math]\displaystyle{ S(t) = q(t) q(t-1) \cdots q(0). }[/math]
Note that here [math]\displaystyle{ q(0) = 1-\operatorname{Prob}(\tau=0\mid\tau \gt -1) = 1-\operatorname{Prob}(\tau=0) }[/math].
The Kaplan–Meier estimator can be seen as a "plug-in estimator" where each [math]\displaystyle{ q(s) }[/math] is estimated based on the data and the estimator of [math]\displaystyle{ S(t) }[/math] is obtained as a product of these estimates.
It remains to specify how [math]\displaystyle{ q(s)=1-\operatorname{Prob}(\tau=s\mid\tau\ge s) }[/math] is to be estimated. By Proposition 1, for any [math]\displaystyle{ k\in [n] }[/math] such that [math]\displaystyle{ c_k\ge s }[/math], [math]\displaystyle{ \operatorname{Prob}(\tau=s) = \operatorname{Prob}(\tilde \tau_k=s) }[/math] and [math]\displaystyle{ \operatorname{Prob}(\tau\ge s) = \operatorname{Prob}(\tilde \tau_k\ge s) }[/math] both hold. Hence, for any [math]\displaystyle{ k\in [n] }[/math] such that [math]\displaystyle{ c_k\ge s }[/math],
- [math]\displaystyle{ \operatorname{Prob}(\tau=s|\tau\ge s) = \operatorname{Prob}(\tilde \tau_k=s)/\operatorname{Prob}(\tilde \tau_k\ge s). }[/math]
By a similar reasoning that lead to the construction of the naive estimator above, we arrive at the estimator
- [math]\displaystyle{ \hat q(s) = 1 - \frac{|\{1\le k\le n\,:\, c_k\ge s, \tilde \tau_k=s\}|}{|\{1\le k \le n\,:\, c_k\ge s, \tilde \tau_k\ge s\}|} = 1 - \frac{|\{1\le k\le n\,:\,\tilde \tau_k=s\}|}{|\{1\le k \le n\,:\, \tilde \tau_k\ge s\}|} }[/math]
(think of estimating the numerator and denominator separately in the definition of the "hazard rate" [math]\displaystyle{ \operatorname{Prob}(\tau=s|\tau\ge s) }[/math]). The Kaplan–Meier estimator is then given by
- [math]\displaystyle{ \hat S(t) = \prod_{s=0}^t \hat q(s). }[/math]
The form of the estimator stated at the beginning of the article can be obtained by some further algebra. For this, write [math]\displaystyle{ \hat q(s)=1-d(s)/n(s) }[/math] where, using the actuarial science terminology, [math]\displaystyle{ d(s)=|\{1\le k\le n\,:\,\tau_k=s\}| }[/math] is the number of known deaths at time [math]\displaystyle{ s }[/math], while [math]\displaystyle{ n(s)=|\{1\le k \le n\,:\, \tilde \tau_k\ge s\}| }[/math] is the number of those persons who are alive (and not being censored) at time [math]\displaystyle{ s-1 }[/math].
Note that if [math]\displaystyle{ d(s)=0 }[/math], [math]\displaystyle{ \hat q(s)=1 }[/math]. This implies that we can leave out from the product defining [math]\displaystyle{ \hat S(t) }[/math] all those terms where [math]\displaystyle{ d(s)=0 }[/math]. Then, letting [math]\displaystyle{ 0\le t_1\lt t_2\lt \dots\lt t_m }[/math] be the times [math]\displaystyle{ s }[/math] when [math]\displaystyle{ d(s)\gt 0 }[/math], [math]\displaystyle{ d_i = d(t_i) }[/math] and [math]\displaystyle{ n_i = n(t_i) }[/math], we arrive at the form of the Kaplan–Meier estimator given at the beginning of the article:
- [math]\displaystyle{ \hat S(t) = \prod_{i:t_i\le t} \left(1-\frac{d_i}{n_i}\right). }[/math]
As opposed to the naive estimator, this estimator can be seen to use the available information more effectively: In the special case mentioned beforehand, when there are many early events recorded, the estimator will multiply many terms with a value below one and will thus take into account that the survival probability cannot be large.
Derivation as a maximum likelihood estimator
Kaplan–Meier estimator can be derived from maximum likelihood estimation of the discrete hazard function.[8][self-published source?] More specifically given [math]\displaystyle{ d_i }[/math] as the number of events and [math]\displaystyle{ n_i }[/math] the total individuals at risk at time [math]\displaystyle{ t_i }[/math], discrete hazard rate [math]\displaystyle{ h_i }[/math] can be defined as the probability of an individual with an event at time [math]\displaystyle{ t_i }[/math]. Then survival rate can be defined as:
- [math]\displaystyle{ S(t) = \prod\limits_{i:\ t_i\le t} (1-h_i) }[/math]
and the likelihood function for the hazard function up to time [math]\displaystyle{ t_i }[/math] is:
- [math]\displaystyle{ \mathcal{L}(h_{j: j\le i}\mid d_{j: j\le i},n_{j: j\le i}) = \prod_{j=1}^i h_j^{d_j}(1-h_j)^{n_j-d_j} {n_j \choose d_j} }[/math]
therefore the log likelihood will be:
- [math]\displaystyle{ \log(\mathcal{L}) = \sum_{j=1}^i \left(d_j\log(h_j)+(n_j-d_j)\log(1-h_j) + \log {n_j \choose d_j} \right) }[/math]
finding the maximum of log likelihood with respect to [math]\displaystyle{ h_i }[/math] yields:
- [math]\displaystyle{ \frac{\partial \log(\mathcal{L})}{\partial h_i} = \frac{d_i}{\widehat{h}_i}-\frac{n_i-d_i}{1-\widehat{h}_i} = 0 \Rightarrow \widehat{h}_i=\frac{d_i}{n_i} }[/math]
where hat is used to denote maximum likelihood estimation. Given this result, we can write:
- [math]\displaystyle{ \widehat S(t) = \prod\limits_{i:\ t_i\le t} \left(1 - \widehat{h}_i\right) = \prod\limits_{i:\ t_i\le t} \left(1 - \frac{d_i}{n_i}\right) }[/math]
More generally (for continuous as well as discrete survival distributions), the Kaplan-Meier estimator may be interpreted as a nonparametric maximum likelihood estimator.[9]
Benefits and limitations
The Kaplan–Meier estimator is one of the most frequently used methods of survival analysis. The estimate may be useful to examine recovery rates, the probability of death, and the effectiveness of treatment. It is limited in its ability to estimate survival adjusted for covariates; parametric survival models and the Cox proportional hazards model may be useful to estimate covariate-adjusted survival.
The Kaplan-Meier estimator is directly related to the Nelson-Aalen estimator and both maximize the empirical likelihood.[10]
Statistical considerations
The Kaplan–Meier estimator is a statistic, and several estimators are used to approximate its variance. One of the most common estimators is Greenwood's formula:[11]
- [math]\displaystyle{ \widehat{\operatorname{Var}} \left( \widehat S(t) \right) = \widehat S(t)^2 \sum_{i:\ t_i\le t} \frac{d_i}{n_i(n_i-d_i)}, }[/math]
where [math]\displaystyle{ d_i }[/math] is the number of cases and [math]\displaystyle{ n_i }[/math] is the total number of observations, for [math]\displaystyle{ t_i \lt t }[/math].
Greenwood's formula is derived[12][self-published source?] by noting that probability of getting [math]\displaystyle{ d_i }[/math] failures out of [math]\displaystyle{ n_i }[/math] cases follows a binomial distribution with failure probability [math]\displaystyle{ h_i }[/math]. As a result for maximum likelihood hazard rate [math]\displaystyle{ \widehat{h}_i = d_i/n_i }[/math] we have [math]\displaystyle{ E\left(\widehat{h}_i\right) = h_i }[/math] and [math]\displaystyle{ \operatorname{Var}\left(\widehat{h}_i\right) = h_i(1-h_i)/n_i }[/math]. To avoid dealing with multiplicative probabilities we compute variance of logarithm of [math]\displaystyle{ \widehat S(t) }[/math] and will use the delta method to convert it back to the original variance:
- [math]\displaystyle{ \begin{align} \operatorname{Var}\left(\log \widehat{S}(t)\right) &\sim \frac{1}{{\widehat{S}(t)}^2} \operatorname{Var} \left(\widehat{S}(t)\right) \Rightarrow \\ \operatorname{Var}\left( \widehat{S}(t)\right) &\sim {{\widehat{S}(t)}^2}\operatorname{Var}\left(\log\widehat{S}(t) \right) \end{align} }[/math]
using martingale central limit theorem, it can be shown that the variance of the sum in the following equation is equal to the sum of variances:[12]
- [math]\displaystyle{ \log\widehat S(t) = \sum\limits_{i:\ t_i\le t} \log\left(1 - \widehat{h}_i\right) }[/math]
as a result we can write:
- [math]\displaystyle{ \begin{align} \operatorname{Var}( \widehat{S}(t)) &\sim {{\widehat{S}(t)}^2}\operatorname{Var}\left(\sum_{i:\ t_i\le t} \log\left(1 - \widehat{h}_i\right)\right) \\ &\sim {{\widehat{S}(t)}^2}\sum\limits_{i:\ t_i\le t} \operatorname{Var}\left(\log\left(1 - \widehat{h}_i\right)\right) \end{align} }[/math]
using the delta method once more:
- [math]\displaystyle{ \begin{align} \operatorname{Var}( \widehat{S}(t)) &\sim {{\widehat{S}(t)}^2}\sum_{i:\ t_i\le t}\left(\frac{\partial \log\left(1 - \widehat{h}_i\right)}{\partial \widehat{h}_i}\right)^2 \operatorname{Var}\left(\widehat{h}_i\right)\\ &={{\widehat{S}(t)}^2}\sum_{i:\ t_i\le t}\left(\frac{1}{1-\widehat{h}_i}\right)^2\frac{\widehat{h}_i \left( 1-\widehat{h}_i \right)}{n_i} \\ &= {{\widehat{S}(t)}^2}\sum_{i:\ t_i\le t} \frac{\widehat{h}_i}{n_i\left(1-\widehat{h}_i\right)} \\ &= {{\widehat{S}(t)}^2}\sum_{i:\ t_i\le t} \frac{d_i}{n_i(n_i-d_i)} \end{align} }[/math]
as desired.
In some cases, one may wish to compare different Kaplan–Meier curves. This can be done by the log rank test, and the Cox proportional hazards test.
Other statistics that may be of use with this estimator are pointwise confidence intervals,[13] the Hall-Wellner band[14] and the equal-precision band.[15]
Software
- Mathematica: the built-in function
SurvivalModelFitcreates survival models.[16] - SAS: The Kaplan–Meier estimator is implemented in the
proc lifetestprocedure.[17] - R: the Kaplan–Meier estimator is available as part of the
survivalpackage.[18][19][20] - Stata: the command
stsreturns the Kaplan–Meier estimator.[21][22] - Python: the
lifelinesandscikit-survivalpackages each include the Kaplan–Meier estimator.[23][24] - MATLAB: the
ecdffunction with the'function','survivor'arguments can calculate or plot the Kaplan–Meier estimator.[25] - StatsDirect: The Kaplan–Meier estimator is implemented in the
Survival Analysismenu.[26] - SPSS: The Kaplan–Meier estimator is implemented in the
Analyze > Survival > Kaplan-Meier...menu.[27] - Julia: the
Survival.jlpackage includes the Kaplan–Meier estimator.[28] - Epi Info: Kaplan–Meier estimator survival curves and results for the log rank test are obtained with the
KMSURVIVALcommand.[29]
See also
- Survival Analysis
- Frequency of exceedance
- Median lethal dose
- Nelson–Aalen estimator
References
- ↑ Kaplan, E. L.; Meier, P. (1958). "Nonparametric estimation from incomplete observations". J. Amer. Statist. Assoc. 53 (282): 457–481. doi:10.2307/2281868.
- ↑ Kaplan, E.L. in a retrospective on the seminal paper in "This week's citation classic". Current Contents 24, 14 (1983). Available from UPenn as PDF.
- ↑ Meyer, Bruce D. (1990). "Unemployment Insurance and Unemployment Spells". Econometrica 58 (4): 757–782. doi:10.2307/2938349. http://www.nber.org/papers/w2546.pdf.
- ↑ Stalpers, Lukas J A; Kaplan, Edward L (4 May 2018). "Edward L. Kaplan and the Kaplan-Meier Survival Curve". BSHM Bulletin: Journal of the British Society for the History of Mathematics 33 (2): 109–135. doi:10.1080/17498430.2018.1450055.
- ↑ Kaplan, E. L.; Meier, Paul (1958). "Nonparametric Estimation from Incomplete Observations". Journal of the American Statistical Association 53 (282): 457–481. doi:10.1080/01621459.1958.10501452. https://www.tandfonline.com/doi/abs/10.1080/01621459.1958.10501452. Retrieved 27 February 2023.
- ↑ "Paul Meier, 1924–2011". Chicago Tribune. August 18, 2011. http://articles.chicagotribune.com/2011-08-18/news/ct-met-meier-obit-20110818_1_clinical-trials-research-experimental-treatment.
- ↑ Rich, Jason T.; Neely, J. Gail; Paniello, Randal C.; Voelker, Courtney C. J.; Nussenbaum, Brian; Wang, Eric W. (September 2010). "A practical guide to understanding Kaplan-Meier curves". Otolaryngology–Head and Neck Surgery 143 (3): 331–336. doi:10.1016/j.otohns.2010.05.007. PMID 20723767.
- ↑ "STAT331 Unit 3". https://web.stanford.edu/~lutian/coursepdf/STAT331unit3.pdf. Retrieved 12 May 2023.
- ↑ Andersen, Per Kragh; Borgan, Ornulf; Gill, Richard D.; Keiding, Niels (1993). Statistical models based on counting processes. New York: Springer-Verlag. ISBN 0-387-97872-0.
- ↑ Zhou, M. (2015). Empirical Likelihood Method in Survival Analysis (1st ed.). Chapman and Hall/CRC. https://doi.org/10.1201/b18598, https://books.google.com/books?id=9-b5CQAAQBAJ&dq=Does+the+Nelson%E2%80%93Aalen+estimator+construct+an+empirical+likelihood%3F&pg=PA7
- ↑ Greenwood, Major (1926). A report on the natural duration of cancer. Issue 33 of Reports on public health and medical subjects. HMSO. OCLC 14713088.
- ↑ 12.0 12.1 "The Greenwood and Exponential Greenwood Confidence Intervals in Survival Analysis". https://www.math.wustl.edu/%7Esawyer/handouts/greenwood.pdf. Retrieved 12 May 2023.
- ↑ Fay, Michael P.; Brittain, Erica H.; Proschan, Michael A. (1 September 2013). "Pointwise confidence intervals for a survival distribution with small samples or heavy censoring". Biostatistics 14 (4): 723–736. doi:10.1093/biostatistics/kxt016. PMID 23632624.
- ↑ Hall, W. J.; Wellner, Jon A. (1980). "Confidence bands for a survival curve from censored data". Biometrika 67 (1): 133–143. doi:10.1093/biomet/67.1.133.
- ↑ Nair, Vijayan N. (August 1984). "Confidence Bands for Survival Functions With Censored Data: A Comparative Study". Technometrics 26 (3): 265–275. doi:10.1080/00401706.1984.10487964.
- ↑ "Survival Analysis – Mathematica SurvivalModelFit". http://reference.wolfram.com/language/ref/SurvivalModelFit.html.
- ↑ "SAS/STAT(R) 14.1 User's Guide". https://support.sas.com/documentation/cdl/en/statug/68162/HTML/default/viewer.htm#statug_lifetest_overview.htm. Retrieved 12 May 2023.
- ↑ Therneau, Terry M. (2022-08-09). "survival: Survival Analysis". The Comprehensive R Archive Network. https://cran.r-project.org/web/packages/survival/index.html.
- ↑ Willekens, Frans (2014). "Statistical Packages for Multistate Life History Analysis". Multistate Analysis of Life Histories with R. Use R!. Springer. pp. 135–153. doi:10.1007/978-3-319-08383-4_6. ISBN 978-3-319-08383-4. https://books.google.com/books?id=Cd2CBAAAQBAJ&pg=PA135.
- ↑ Chen, Ding-Geng; Peace, Karl E. (2014). Clinical Trial Data Analysis Using R. CRC Press. pp. 99–108. ISBN 9781439840214. https://books.google.com/books?id=fGnRBQAAQBAJ&pg=PA99.
- ↑ "sts — Generate, graph, list, and test the survivor and cumulative hazard functions". Stata Manual. https://www.stata.com/manuals15/ststs.pdf.
- ↑ Cleves, Mario (2008). An Introduction to Survival Analysis Using Stata (Second ed.). College Station: Stata Press. pp. 93–107. ISBN 978-1-59718-041-2. https://books.google.com/books?id=xttbn0a-QR8C&pg=PA93.
- ↑ "lifelines — lifelines 0.27.7 documentation". https://lifelines.readthedocs.io/en/latest/. Retrieved 12 May 2023.
- ↑ "sksurv.nonparametric.kaplan_meier_estimator — scikit-survival 0.20.0". https://scikit-survival.readthedocs.io/en/stable/api/generated/sksurv.nonparametric.kaplan_meier_estimator.html. Retrieved 12 May 2023.
- ↑ "Empirical cumulative distribution function – MATLAB ecdf". http://mathworks.com/help/stats/ecdf.html.
- ↑ "Kaplan-Meier Survival Estimates". https://www.statsdirect.co.uk/help/Default.htm#survival_analysis/kaplan_meier.htm.
- ↑ "Kaplan-Meier method in SPSS Statistics | Laerd Statistics". https://statistics.laerd.com/spss-tutorials/kaplan-meier-using-spss-statistics.php.
- ↑ "Kaplan-Meier · Survival.jl". https://juliastats.org/Survival.jl/latest/km/.
- ↑ "Epi Info™ User Guide - Command Reference - Analysis Commands: KMSURVIVAL". https://www.cdc.gov/epiinfo/user-guide/command-reference/analysis-commands-kmsurvival.html. Retrieved 30 Oct 2023.
Further reading
- Aalen, Odd; Borgan, Ornulf; Gjessing, Hakon (2008). Survival and Event History Analysis: A Process Point of View. Springer. pp. 90–104. ISBN 978-0-387-68560-1.
- Greene, William H. (2012). "Nonparametric and Semiparametric Approaches". Econometric Analysis (Seventh ed.). Prentice-Hall. pp. 909–912. ISBN 978-0-273-75356-8. https://books.google.com/books?id=-WFPYgEACAAJ&pg=PA909.
- Jones, Andrew M.; Rice, Nigel; D'Uva, Teresa Bago; Balia, Silvia (2013). "Duration Data". Applied Health Economics. London: Routledge. pp. 139–181. ISBN 978-0-415-67682-3. https://books.google.com/books?id=7tdcCol9mNEC&pg=PA141.
- Singer, Judith B.; Willett, John B. (2003). Applied Longitudinal Data Analysis: Modeling Change and Event Occurrence. New York: Oxford University Press. pp. 483–487. ISBN 0-19-515296-4. https://books.google.com/books?id=PpnA1M8VwR8C&pg=PA483.
External links
- Dunn, Steve (2002). "Survival Curves: Accrual and The Kaplan–Meier Estimate". http://www.cancerguide.org/scurve_km.html.
 |