Estimation statistics
Estimation statistics, or simply estimation, is a data analysis framework that uses a combination of effect sizes, confidence intervals, precision planning, and meta-analysis to plan experiments, analyze data and interpret results.[1] It complements hypothesis testing approaches such as null hypothesis significance testing (NHST), by going beyond the question is an effect present or not, and provides information about how large an effect is.[2][3] Estimation statistics is sometimes referred to as the new statistics.[3][4][5]
The primary aim of estimation methods is to report an effect size (a point estimate) along with its confidence interval, the latter of which is related to the precision of the estimate.[6] The confidence interval summarizes a range of likely values of the underlying population effect. Proponents of estimation see reporting a P value as an unhelpful distraction from the important business of reporting an effect size with its confidence intervals,[7] and believe that estimation should replace significance testing for data analysis.[8][9]
History
Starting in 1929, physicist Raymond Thayer Birge published review papers[10] in which he used weighted-averages methods to calculate estimates of physical constants, a procedure that can be seen as the precursor to modern meta-analysis.[11]
In the 1930s Jerzy Neyman published a series of papers on statistical estimation where he defined the mathematics and terminology of confidence intervals. [12][13][14]
In the 1960s, estimation statistics was adopted by the non-physical sciences with the development of the standardized effect size by Jacob Cohen.
In the 1970s, modern research synthesis was pioneered by Gene V. Glass with the first systematic review and meta-analysis for psychotherapy.[15] This pioneering work subsequently influenced the adoption of meta-analyses for medical treatments more generally.
In the 1980s and 1990s, estimation methods were extended and refined for practical application by biostatisticians including Larry Hedges, Michael Borenstein, Doug Altman, Martin Gardner, and many others, with the development of the modern (medical) meta-analysis.
Starting in the 1980s, the systematic review, used in conjunction with meta-analysis, became a technique widely used in medical research. There are over 200,000 citations to "meta-analysis" in PubMed.
In the 1990s, editor Kenneth Rothman banned the use of p-values from the journal Epidemiology; compliance was high among authors but this did not substantially change their analytical thinking.[16]
In the 2010s, Geoff Cumming published a textbook dedicated to estimation statistics, along with software in Excel designed to teach effect-size thinking, primarily to psychologists.[17] Also in the 2010s, estimation methods were increasingly adopted in neuroscience.[18][19]
In 2013, the Publication Manual of the American Psychological Association recommended to use estimation in addition to hypothesis testing.[20] Also in 2013, the Uniform Requirements for Manuscripts Submitted to Biomedical Journals document made a similar recommendation: "Avoid relying solely on statistical hypothesis testing, such as P values, which fail to convey important information about effect size."[21]
In 2019, over 800 scientists signed an open comment calling for the entire concept of statistical significance to be abandoned.[22]
In 2019, the Society for Neuroscience journal eNeuro instituted a policy recommending the use of estimation graphics as the preferred method for data presentation.[23] And in 2022, the International Society of Physiotherapy Journal Editors recommended the use of estimation methods instead of null hypothesis statistical tests.[24]
Despite the widespread adoption of meta-analysis for clinical research, and recommendations by several major publishing institutions, the estimation framework is not routinely used in primary biomedical research.[25]
Methodology
Many significance tests have an estimation counterpart;[26] in almost every case, the test result (or its p-value) can be simply substituted with the effect size and a precision estimate. For example, instead of using Student's t-test, the analyst can compare two independent groups by calculating the mean difference and its 95% confidence interval. Corresponding methods can be used for a paired t-test and multiple comparisons. Similarly, for a regression analysis, an analyst would report the coefficient of determination (R2) and the model equation instead of the model's p-value.
However, proponents of estimation statistics warn against reporting only a few numbers. Rather, it is advised to analyze and present data using data visualization.[2][5][6] Examples of appropriate visualizations include the scatter plot for regression, and Gardner–Altman plots for two independent groups.[27] While historical data-group plots (bar charts, box plots, and violin plots) do not display the comparison, estimation plots add a second axis to explicitly visualize the effect size.[28]
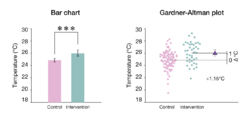
Gardner–Altman plot
The Gardner–Altman mean difference plot was first described by Martin Gardner and Doug Altman in 1986;[27] it is a statistical graph designed to display data from two independent groups.[5] There is also a version suitable for paired data. The key instructions to make this chart are as follows: (1) display all observed values for both groups side-by-side; (2) place a second axis on the right, shifted to show the mean difference scale; and (3) plot the mean difference with its confidence interval as a marker with error bars.[3] Gardner-Altman plots can be generated with DABEST-Python, or dabestr; alternatively, the analyst can use GUI software like the Estimation Stats app.
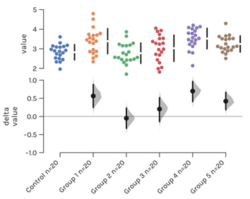
Cumming plot
For multiple groups, Geoff Cumming introduced the use of a secondary panel to plot two or more mean differences and their confidence intervals, placed below the observed values panel;[3] this arrangement enables easy comparison of mean differences ('deltas') over several data groupings. Cumming plots can be generated with the ESCI package, DABEST, or the Estimation Stats app.
Other methodologies
In addition to the mean difference, there are numerous other effect size types, all with relative benefits. Major types include effect sizes in the Cohen's d class of standardized metrics, and the coefficient of determination (R2) for regression analysis. For non-normal distributions, there are a number of more robust effect sizes, including Cliff's delta and the Kolmogorov-Smirnov statistic.
Flaws in hypothesis testing
In hypothesis testing, the primary objective of statistical calculations is to obtain a p-value, the probability of seeing an obtained result, or a more extreme result, when assuming the null hypothesis is true. If the p-value is low (usually < 0.05), the statistical practitioner is then encouraged to reject the null hypothesis. Proponents of estimation reject the validity of hypothesis testing[3][6] for the following reasons, among others:
- P-values are easily and commonly misinterpreted. For example, the p-value is often mistakenly thought of as 'the probability that the null hypothesis is true.'
- The null hypothesis is always wrong for every set of observations: there is always some effect, even if it is minuscule.[29]
- Hypothesis testing produces dichotomous yes-no answers, while discarding important information about magnitude.[30]
- Any particular p-value arises through the interaction of the effect size, the sample size (all things being equal a larger sample size produces a smaller p-value) and sampling error.[31]
- At low power, simulation reveals that sampling error makes p-values extremely volatile.[32]
Benefits of estimation statistics
Quantification
While p-values focus on yes/no answers, estimation directs the analyst's attention to quantification.
Advantages of confidence intervals
Confidence intervals behave in a predictable way. By definition, 95% confidence intervals have a 95% chance of covering the underlying population mean (μ). This feature remains constant with increasing sample size; what changes is that the interval becomes smaller. In addition, 95% confidence intervals are also 83% prediction intervals: one (pre experimental) confidence interval has an 83% chance of covering any future experiment's mean.[3] As such, knowing a single experiment's 95% confidence intervals gives the analyst a reasonable range for the population mean. Nevertheless, confidence distributions and posterior distributions provide a whole lot more information than a single point estimate or intervals,[33] that can exacerbate dichotomous thinking according to the interval covering or not covering a "null" value of interest (i.e. the Inductive behavior of Neyman as opposed to that of Fisher[34]).
Evidence-based statistics
Psychological studies of the perception of statistics reveal that reporting interval estimates leaves a more accurate perception of the data than reporting p-values.[35]
Precision planning
The precision of an estimate is formally defined as 1/variance, and like power, increases (improves) with increasing sample size. Like power, a high level of precision is expensive; research grant applications would ideally include precision/cost analyses. Proponents of estimation believe precision planning should replace power since statistical power itself is conceptually linked to significance testing.[3] Precision planning can be done with the ESCI web app.
See also
References
- ↑ Ellis, Paul. "Effect size FAQ". http://effectsizefaq.com/.
- ↑ 2.0 2.1 Cohen, Jacob. "The earth is round (p<.05)". https://www.ics.uci.edu/~sternh/courses/210/cohen94_pval.pdf.
- ↑ 3.0 3.1 3.2 3.3 3.4 3.5 3.6 Cumming, Geoff (2011). Understanding The New Statistics: Effect Sizes, Confidence Intervals, and Meta-Analysis. New York: Routledge. ISBN 978-0-415-87967-5.[page needed]
- ↑ Altman, Douglas (1991). Practical Statistics For Medical Research. London: Chapman and Hall. https://archive.org/details/isbn_9780412276309.
- ↑ 5.0 5.1 5.2 Douglas Altman, ed (2000). Statistics with Confidence. London: Wiley-Blackwell.[page needed]
- ↑ 6.0 6.1 6.2 Cohen, Jacob (1990). "Things I have learned (so far)". American Psychologist 45 (12): 1304–1312. doi:10.1037/0003-066x.45.12.1304. http://revistas.um.es/analesps/article/view/28521.
- ↑ Ellis, Paul (2010-05-31). "Why can't I just judge my result by looking at the p value?". http://effectsizefaq.com/2010/05/31/why-can%E2%80%99t-i-just-judge-my-result-by-looking-at-the-p-value/.
- ↑ Claridge-Chang, Adam; Assam, Pryseley N (2016). "Estimation statistics should replace significance testing". Nature Methods 13 (2): 108–109. doi:10.1038/nmeth.3729. PMID 26820542. https://zenodo.org/record/60156.
- ↑ Berner, Daniel; Amrhein, Valentin (2022). "Why and how we should join the shift from significance testing to estimation" (in en). Journal of Evolutionary Biology 35 (6): 777–787. doi:10.1111/jeb.14009. ISSN 1010-061X. PMID 35582935.
- ↑ Birge, Raymond T. (1929). "Probable Values of the General Physical Constants". Reviews of Modern Physics 1 (1): 1–73. doi:10.1103/RevModPhys.1.1. Bibcode: 1929RvMP....1....1B.
- ↑ Hedges, Larry (1987). "How hard is hard science, how soft is soft science". American Psychologist 42 (5): 443. doi:10.1037/0003-066x.42.5.443.
- ↑ Neyman, J. (1934). On the Two Different Aspects of the Representative Method: The Method of Stratified Sampling and the Method of Purposive Selection. Journal of the Royal Statistical Society, 97(4), 558–625. https://doi.org/10.2307/2342192 (see Note I in the appendix)
- ↑ J. Neyman (1935), Ann. Math. Statist. 6(3): 111-116 (September, 1935). https://doi.org/10.1214/aoms/1177732585
- ↑ Neyman, J. (1937). "Outline of a Theory of Statistical Estimation Based on the Classical Theory of Probability". Philosophical Transactions of the Royal Society A. 236 (767): 333–380. Bibcode:1937RSPTA.236..333N. doi:10.1098/rsta.1937.0005. JSTOR 91337.
- ↑ Hunt, Morton (1997). How science takes stock: the story of meta-analysis. New York: The Russell Sage Foundation. ISBN 978-0-87154-398-1.
- ↑ Fidler, Fiona; Thomason, Neil; Cumming, Geoff; Finch, Sue; Leeman, Joanna (2004). "Editors Can Lead Researchers to Confidence Intervals, but Can't Make Them Think: Statistical Reform Lessons From Medicine". Psychological Science 15 (2): 119–126. doi:10.1111/j.0963-7214.2004.01502008.x. PMID 14738519.
- ↑ Cumming, Geoff. "ESCI (Exploratory Software for Confidence Intervals)". http://www.latrobe.edu.au/psy/research/projects/esci.
- ↑ Yildizoglu, Tugce; Weislogel, Jan-Marek; Mohammad, Farhan; Chan, Edwin S.-Y.; Assam, Pryseley N.; Claridge-Chang, Adam (2015). "Estimating Information Processing in a Memory System: The Utility of Meta-analytic Methods for Genetics". PLOS Genetics 11 (12). doi:10.1371/journal.pgen.1005718. PMID 26647168.
- ↑ Hentschke, Harald; Maik C. Stüttgen (2011). "Computation of measures of effect size for neuroscience data sets". European Journal of Neuroscience 34 (12): 1887–1894. doi:10.1111/j.1460-9568.2011.07902.x. PMID 22082031.
- ↑ "Publication Manual of the American Psychological Association, Sixth Edition". http://www.apastyle.org/manual/index.aspx.
- ↑ "Uniform Requirements for Manuscripts Submitted to Biomedical Journals". http://www.icmje.org/manuscript_1prepare.html.
- ↑ Amrhein, Valentin; Greenland, Sander; McShane, Blake (2019). "Scientists rise up against statistical significance", Nature 567, 305-307.
- ↑ Bernard, Christophe (2019). "Changing the Way We Report, Interpret, and Discuss Our Results to Rebuild Trust in Our Research". eNeuro 6 (4). doi:10.1523/ENEURO.0259-19.2019. PMID 31453315.
- ↑ Elkins, Mark; et al. (2022). "Statistical inference through estimation: recommendations from the International Society of Physiotherapy Journal Editors", Journal of Physiotherapy, 68 (1), 1-4.
- ↑ Halsey, Lewis G. (2019). "The reign of the p -value is over: what alternative analyses could we employ to fill the power vacuum?". Biology Letters 15 (5). doi:10.1098/rsbl.2019.0174. PMID 31113309.
- ↑ Cumming, Geoff; Calin-Jageman, Robert (2016). Introduction to the New Statistics: Estimation, Open Science, and Beyond. Routledge. ISBN 978-1-138-82552-9.[page needed]
- ↑ 27.0 27.1 Gardner, M J; Altman, D G (1986). "Confidence intervals rather than P values: estimation rather than hypothesis testing.". BMJ 292 (6522): 746–750. doi:10.1136/bmj.292.6522.746. PMID 3082422.
- ↑ Ho, Joses; Tumkaya, Tayfun; Aryal, Sameer; Choi, Hyungwon; Claridge-Chang, Adam (2018). Moving beyond P values: Everyday data analysis with estimation plots. doi:10.1101/377978.
- ↑ Cohen, Jacob (1994). "The earth is round (p < .05).". American Psychologist 49 (12): 997–1003. doi:10.1037/0003-066X.49.12.997.
- ↑ Ellis, Paul (2010). The Essential Guide to Effect Sizes: Statistical Power, Meta-Analysis, and the Interpretation of Research Results. Cambridge: Cambridge University Press.[page needed]
- ↑ Denton E. Morrison, Ramon E. Henkel, ed (2006). The Significance Test Controversy: A Reader. Aldine Transaction. ISBN 978-0-202-30879-1.[page needed]
- ↑ Cumming, Geoff (3 March 2009). "Dance of the p values". https://www.youtube.com/watch?v=ez4DgdurRPg.
- ↑ Xie, Min-ge; Singh, Kesar (2013). "Confidence Distribution, the Frequentist Distribution Estimator of a Parameter: A Review". International Statistical Review 81 (1): 3–39. doi:10.1111/insr.12000.
- ↑ Halpin, Peter F.; Stam, Henderikus J. (2006). "Inductive Inference or Inductive Behavior: Fisher and Neyman: Pearson Approaches to Statistical Testing in Psychological Research (1940-1960)". The American Journal of Psychology 119 (4): 625–653. doi:10.2307/20445367. PMID 17286092.
- ↑ Beyth-Marom, Ruth; Fidler, Fiona Margaret; Cumming, Geoffrey David (2008). "Statistical cognition: Towards evidence-based practice in statistics and statistics education". Statistics Education Research Journal 7 (2): 20–39. doi:10.52041/serj.v7i2.468.
 |
